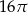Na rysunku przedstawiony jest czworościan foremny 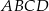 , którego objętość i pole powierzchni całkowitej są odpowiednio równe:
, którego objętość i pole powierzchni całkowitej są odpowiednio równe: 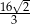 i
i 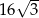 .
.
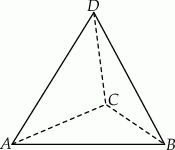
Promień okręgu wpisanego w ścianę 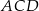 jest równy
jest równy
A) 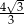 B)
B) 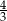 C)
C) 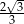 D)
D) 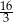
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiony jest czworościan foremny 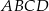 , którego objętość i pole powierzchni całkowitej są odpowiednio równe:
, którego objętość i pole powierzchni całkowitej są odpowiednio równe: 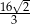 i
i 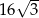 .
.

Promień okręgu wpisanego w ścianę 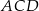 jest równy
jest równy
A) 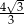 B)
B) 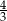 C)
C) 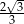 D)
D) 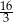
Dany jest stożek, którego przekrojem osiowym jest trójkąt o bokach długości: 6, 10 i 10. Stosunek pola powierzchni bocznej stożka do pola jego podstawy jest równy
A) 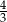 B)
B) 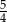 C)
C) 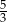 D)
D) 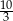
Pole powierzchni bocznej stożka jest dwa razy większe od jego pola podstawy. Tworząca tego stożka jest nachylona do płaszczyzny podstawy pod kątem
A) 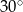 B)
B) 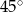 C)
C) 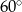 D)
D) 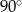
Pole powierzchni bocznej walca jest równe 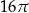 , a promień jego podstawy ma długość 2. Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych. Objętość tego walca jest równa A) 16 B) 32 C)
, a promień jego podstawy ma długość 2. Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych. Objętość tego walca jest równa A) 16 B) 32 C) 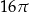 D)
D) 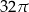
Przekątna sześcianu jest o 3 dłuższa od długości jego krawędzi. Długość krawędzi sześcianu jest równa
A) 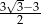 B)
B) 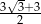 C)
C) 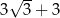 D)
D) 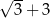
Pole powierzchni całkowitej pewnego stożka jest 5 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 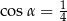 B)
B) 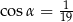 C)
C) 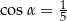 D)
D) 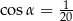
Stosunek objętości dwóch sześcianów jest równy 1 : 27. Zatem stosunek długości krawędzi tych sześcianów wynosi:
A) 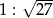 B) 1:3 C) 1:9 D) 1:27
B) 1:3 C) 1:9 D) 1:27
Stosunek objętości dwóch sześcianów jest równy 1 : 125. Zatem stosunek długości krawędzi tych sześcianów wynosi:
A) 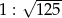 B) 1:125 C) 1:25 D) 1:5
B) 1:125 C) 1:25 D) 1:5
W ostrosłupie czworokątnym, w którym wszystkie krawędzie mają tę samą długość, kąt nachylenia krawędzi bocznej do płaszczyzny podstawy ma miarę
A) 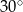 B)
B) 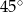 C)
C) 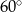 D)
D) 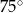
Podstawą ostrosłupa prawidłowego czworokątnego  jest kwadrat
jest kwadrat 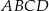 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
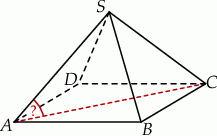
Miara kąta 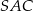 jest równa
jest równa
A) 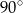 B)
B) 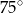 C)
C) 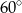 D)
D) 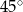
W ostrosłupie prawidłowym czworokątnym, w którym wszystkie krawędzie mają tę samą długość, kąt między wysokością ostrosłupa, a jego krawędzią boczną ma miarę
A) 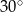 B)
B) 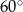 C)
C) 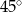 D)
D) 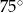
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 6.
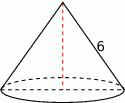
Pole powierzchni bocznej tego stożka jest równe
A) 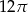 B)
B) 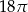 C)
C) 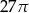 D)
D) 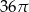
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 8.
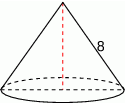
Pole powierzchni bocznej tego stożka jest równe
A) 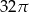 B)
B) 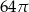 C)
C) 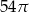 D)
D) 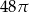
Pole powierzchni bocznej stożka o kącie rozwarcia 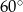 i promieniu podstawy 3 cm jest równe
i promieniu podstawy 3 cm jest równe
A) 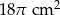 B)
B) 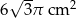 C)
C) 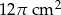 D)
D) 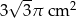
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 4.
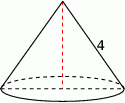
Pole powierzchni bocznej tego stożka jest równe
A) 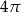 B)
B) 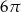 C)
C) 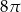 D)
D) 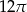
Szklane naczynie w kształcie stożka o promieniu podstawy 6 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
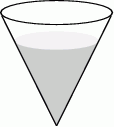
Objętość wody w naczyniu jest równa
A) 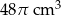 B)
B) 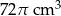 C)
C) 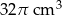 D)
D) 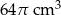
Szklane naczynie w kształcie stożka o promieniu podstawy 8 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
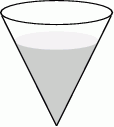
Objętość wody w naczyniu jest równa
A) 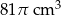 B)
B) 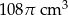 C)
C) 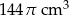 D)
D) 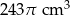
Przekrój osiowy walca jest kwadratem o polu 8. Pole powierzchni całkowitej tego walca jest równe
A) 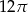 B)
B) 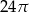 C)
C) 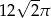 D)
D) 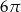
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli  oznacza promień podstawy walca,
oznacza promień podstawy walca, 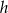 oznacza wysokość walca, to
oznacza wysokość walca, to
A) 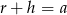 B)
B) 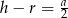 C)
C) 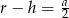 D)
D) 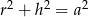
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli 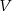 oznacza objętość walca,
oznacza objętość walca, 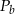 oznacza pole powierzchni bocznej walca, to
oznacza pole powierzchni bocznej walca, to
A) 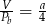 B)
B) 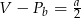 C)
C) 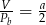 D)
D) 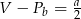
Dany jest graniastosłup prawidłowy sześciokątny 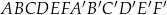 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 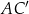 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 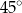 (zobacz rysunek).
(zobacz rysunek).

Objętość tego graniastosłupa jest równa
A) 225 B) 562,5 C) 112,5 D) 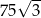
Na rysunku przedstawiony jest czworościan foremny  , którego objętość i pole powierzchni całkowitej są odpowiednio równe:
, którego objętość i pole powierzchni całkowitej są odpowiednio równe: 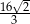 i
i 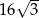 .
.
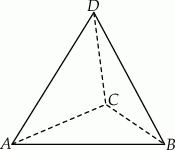
Wysokość czworościanu 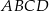 jest równa
jest równa
A) 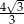 B)
B) 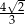 C)
C) 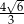 D)
D) 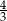
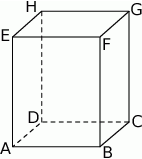
Dany jest graniastosłup prawidłowy czworokątny (patrz rysunek). Podaj oznaczenie kąta zawartego między przekątną graniastosłupa i krawędzią podstawy.
A) 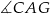 B)
B) 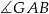 C)
C) 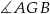 D)
D) 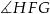
Promień sfery opisanej na sześcianie jest równy 6. Długość krawędzi tego sześcianu jest równa
A) 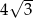 B)
B) 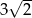 C)
C) 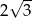 D)
D) 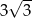
Kąt  nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
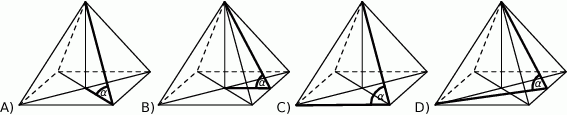
Kąt  nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
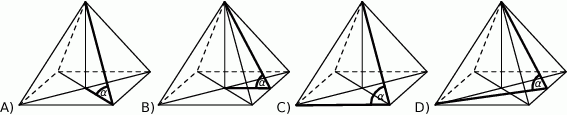
Objętość walca o promieniu podstawy  i wysokości 2 razy większej od promienia jest równa
i wysokości 2 razy większej od promienia jest równa
A) 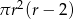 B)
B) 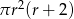 C)
C) 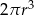 D)
D) 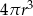
Objętość walca o promieniu podstawy  i wysokości 4 razy mniejszej od promienia jest równa
i wysokości 4 razy mniejszej od promienia jest równa
A) 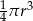 B)
B) 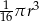 C)
C) 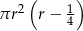 D)
D) 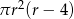
Objętość walca o promieniu podstawy  i wysokości 3 razy większej od promienia jest równa
i wysokości 3 razy większej od promienia jest równa
A) 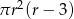 B)
B) 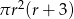 C)
C) 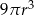 D)
D) 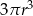
Objętość walca o promieniu podstawy  i wysokości 2 razy mniejszej od promienia jest równa
i wysokości 2 razy mniejszej od promienia jest równa
A) 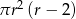 B)
B) 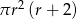 C)
C) 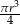 D)
D) 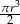
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia o dwa większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia o dwa większa. Objętość tego walca jest równa
A) 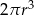 B)
B) 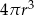 C)
C) 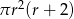 D)
D) 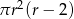
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
A) 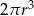 B)
B) 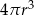 C)
C) 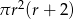 D)
D) 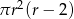
Stożek o promieniu podstawy  i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
A) 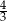 B) 12 C)
B) 12 C) 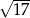 D) 4
D) 4
Stożek o średnicy podstawy 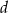 i kula o promieniu
i kula o promieniu 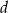 mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
A) 32 B)  C)
C) 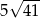 D) 4
D) 4
Objętość walca o promieniu podstawy 4 jest równa 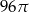 . Pole powierzchni bocznej tego walca jest równe
. Pole powierzchni bocznej tego walca jest równe
A) 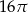 B)
B) 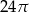 C)
C) 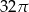 D)
D) 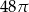
Objętość walca o promieniu podstawy 3 jest równa 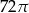 . Pole powierzchni bocznej tego walca jest równe
. Pole powierzchni bocznej tego walca jest równe
A) 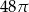 B)
B) 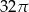 C)
C) 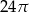 D)
D)