Przedstawiona na rysunku bryła składa się z walca i półkuli. Wysokość walca jest taka, jak promień jego podstawy i jest równa 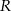 .
.
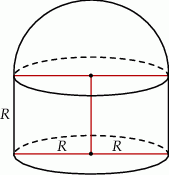
Objętość tej bryły jest równa
A) 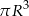 B)
B) 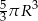 C)
C) 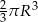 D)
D) 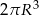
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Przedstawiona na rysunku bryła składa się z walca i półkuli. Wysokość walca jest taka, jak promień jego podstawy i jest równa 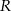 .
.

Objętość tej bryły jest równa
A) 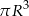 B)
B) 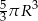 C)
C) 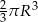 D)
D) 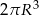
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa  i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
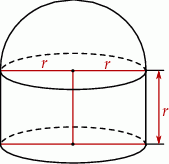
Pole powierzchni całkowitej tej bryły jest równe
A) 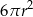 B)
B) 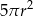 C)
C) 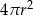 D)
D) 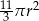
Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa  i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.
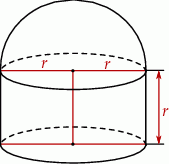
Objętość tej bryły jest równa
A) 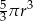 B)
B) 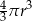 C)
C) 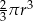 D)
D) 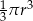
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 6. Objętość tego stożka jest równa
A) 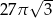 B)
B) 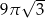 C)
C) 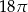 D)
D) 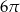
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 4. Objętość tego stożka jest równa
A) 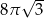 B)
B) 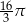 C)
C) 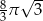 D)
D) 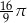
W prostopadłościanie o objętości 3400 skrócono o 10% najkrótsze krawędzie, a następnie wydłużono najdłuższe krawędzie tak, aby otrzymany prostopadłościan miał objętość 3519. O ile procent wydłużono najdłuższe krawędzie prostopadłościanu?
A) 18% B) 12% C) 15% D) 20%
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 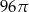 B)
B) 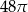 C)
C) 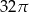 D)
D) 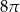
Dany jest stożek o wysokości 6 i tworzącej 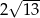 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 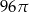 B)
B) 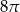 C)
C) 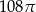 D)
D) 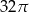
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół krótszej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 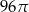 B)
B) 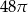 C)
C) 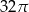 D)
D) 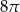
Dany jest stożek o wysokości 6 i tworzącej 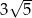 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 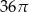 B)
B) 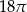 C)
C) 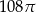 D)
D) 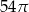
Pole powierzchni bocznej stożka wynosi 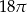 . Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
A) 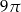 B)
B) 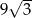 C)
C) 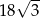 D)
D) 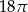
Pole powierzchni bocznej stożka wynosi 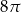 . Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
A) 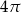 B)
B) 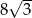 C)
C) 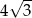 D)
D) 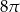
Graniastosłup ma 15 krawędzi. Ile wierzchołków ma ten graniastosłup?
A) 10 B) 5 C) 15 D) 30
Liczba wszystkich krawędzi graniastosłupa jest równa 42. Liczba wszystkich wierzchołków tego graniastosłupa jest równa
A) 14 B) 28 C) 15 D) 42
Graniastosłup ma 18 krawędzi. Ile wierzchołków ma ten graniastosłup?
A) 18 B) 6 C) 12 D) 24
Liczba wszystkich krawędzi graniastosłupa jest równa 24. Wtedy liczba wszystkich jego wierzchołków jest równa
A) 6 B) 8 C) 12 D) 16
Pole powierzchni całkowitej czworościanu foremnego jest równe 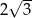 . Suma długości krawędzi tego czworościanu jest równa
. Suma długości krawędzi tego czworościanu jest równa
A) 12 B) 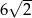 C)
C) 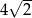 D)
D) 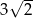
Pole powierzchni całkowitej czworościanu foremnego jest równe 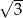 . Suma długości krawędzi tego czworościanu jest równa
. Suma długości krawędzi tego czworościanu jest równa
A) 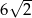 B) 3 C) 4 D) 6
B) 3 C) 4 D) 6
Na rysunku przedstawiono siatkę czworościanu foremnego.
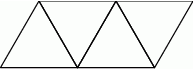
Jeżeli pole powierzchni całkowitej tego czworościanu jest równe 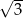 , to suma długości jego krawędzi jest równa
, to suma długości jego krawędzi jest równa
A) 9 B) 6 C) 4 D) 3
Dany jest prostopadłościan o wymiarach 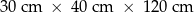 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 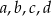 , o długościach – odpowiednio – 119 cm, 121 cm, 129 cm i 131 cm.
, o długościach – odpowiednio – 119 cm, 121 cm, 129 cm i 131 cm.
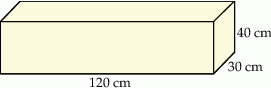
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 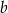 .
.
C) tylko od odcinków 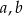 i
i  .
.
D) od wszystkich czterech danych odcinków.
Dany jest prostopadłościan o wymiarach 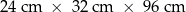 (zobacz rysunek), a ponadto dane są cztery odcinki
(zobacz rysunek), a ponadto dane są cztery odcinki 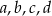 , o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
, o długościach – odpowiednio – 89 cm, 101 cm, 110 cm i 121 cm.
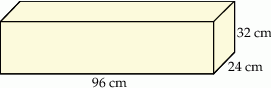
Przekątna tego prostopadłościanu jest dłuższa
A) tylko od odcinka  .
.
B) tylko od odcinków  i
i 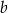 .
.
C) tylko od odcinków 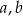 i
i  .
.
D) od wszystkich czterech danych odcinków.
Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą 6. Cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa jest równy
A) 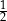 B)
B) 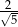 C)
C) 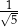 D)
D) 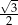
Pole powierzchni całkowitej prostopadłościanu o wymiarach 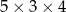 jest równe
jest równe
A) 94 B) 60 C) 47 D) 20
Pole powierzchni całkowitej prostopadłościanu o wymiarach 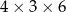 jest równe
jest równe
A) 94 B) 54 C) 108 D) 72
Dany jest sześcian 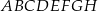 . Przekątne
. Przekątne 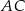 i
i 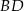 ściany
ściany 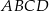 sześcianu przecinają się w punkcie
sześcianu przecinają się w punkcie 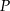 (zobacz rysunek).
(zobacz rysunek).
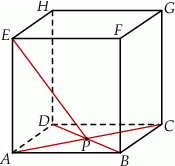
Tangens kąta, jaki odcinek 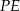 tworzy z płaszczyzną
tworzy z płaszczyzną 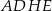 , jest równy
, jest równy
A) 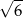 B)
B) 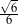 C)
C) 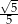 D)
D) 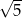
Gdy dodamy liczbę wszystkich krawędzi pewnego graniastosłupa do liczby wszystkich jego wierzchołków, to otrzymamy w wyniku 15. Liczba wszystkich krawędzi tego graniastosłupa jest równa
A) 9 B) 7 C) 6 D) 5
Gdy dodamy liczbę wszystkich krawędzi pewnego graniastosłupa do liczby wszystkich jego wierzchołków, to otrzymamy w wyniku 25. Liczba wszystkich krawędzi tego graniastosłupa jest równa
A) 9 B) 5 C) 6 D) 15
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie 8 i ramieniu 10. Powierzchnia boczna stożka jest wycinkiem koła o kącie środkowym
A) 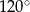 B)
B) 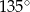 C)
C) 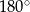 D)
D) 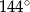
Liczba ścian graniastosłupa, który ma 14 wierzchołków, jest równa
A) 7 B) 5 C) 9 D) 11
Liczba ścian graniastosłupa, który ma 16 wierzchołków, jest równa
A) 12 B) 10 C) 9 D) 8
Liczba ścian graniastosłupa, który ma 20 wierzchołków, jest równa
A) 12 B) 10 C) 5 D) 8
Krawędź podstawy ostrosłupa prawidłowego czworokątnego ma długość 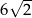 , a krawędź boczna ma długość 10. Wysokość ostrosłupa ma długość
, a krawędź boczna ma długość 10. Wysokość ostrosłupa ma długość
A) 6 B) 8 C) 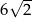 D)
D) 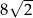
Przekątna przekroju osiowego walca, którego promień podstawy jest równy 4 i wysokość jest równa 6, ma długość
A) 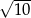 B)
B) 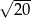 C)
C) 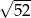 D) 10
D) 10
Przekątna przekroju osiowego walca, którego promień podstawy jest równy 6 i wysokość jest równa 9, ma długość
A) 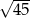 B) 15 C)
B) 15 C) 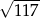 D) 10
D) 10
Objętość ostrosłupa prawidłowego czworokątnego jest równa 64. Wysokość tego ostrosłupa jest równa 12. Długość krawędzi podstawy tego ostrosłupa jest równa
A) 2 B) 4 C) 6 D) 8
Która z podanych liczb nie może być liczbą krawędzi graniastosłupa?
A) 37035 B) 13629 C) 17023 D) 26919
Która z podanych liczb nie może być liczbą krawędzi graniastosłupa?
A) 67035 B) 49629 C) 17022 D) 16919
Objętość sześcianu, w którym przekątna ściany bocznej ma długość 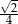 , jest równa
, jest równa
A) 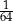 B)
B) 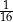 C) 16 D) 64
C) 16 D) 64
Przekątna ściany sześcianu ma długość 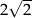 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 8 B) 24 C) 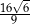 D)
D) 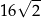
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość. Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
A) 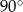 B)
B) 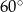 C)
C) 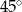 D)
D) 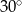
W ostrosłupie prawidłowym czworokątnym stosunek długości krawędzi bocznej do długości krawędzi podstawy wynosi 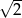 . Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
. Wobec tego kąt między dwiema przeciwległymi krawędziami bocznymi ma miarę
A) 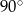 B)
B) 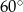 C)
C) 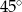 D)
D) 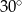
Podstawą ostrosłupa prawidłowego czworokątnego 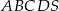 jest kwadrat
jest kwadrat 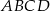 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta 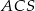 jest równa
jest równa
A) 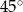 B)
B) 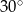 C)
C) 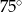 D)
D) 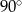
Podstawą ostrosłupa prawidłowego czworokątnego 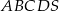 jest kwadrat
jest kwadrat 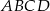 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta 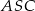 jest równa
jest równa
A) 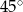 B)
B) 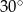 C)
C) 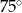 D)
D) 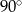
Podstawą ostrosłupa prawidłowego czworokątnego 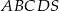 jest kwadrat
jest kwadrat 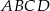 . Jaka jest miara kąta
. Jaka jest miara kąta 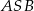 jeżeli trójkąt
jeżeli trójkąt 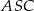 jest prostokątny?
jest prostokątny?
A) 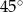 B)
B) 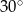 C)
C) 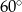 D)
D)