Na giełdzie kupiono tę samą liczbę akcji dwóch przedsiębiorstw, przy czym średnia cena zakupu jednej akcji drugiego przedsiębiorstwa była dwa razy wyższa od średniej ceny akcji pierwszego przedsiębiorstwa. Ile średnio zapłacono za jedną akcję drugiego przedsiębiorstwa, jeżeli średnia cena zakupu wszystkich akcji wyniosła 90 zł?
A) 30 zł B) 60 zł C) 90 zł D) 120 zł
/Szkoła średnia/Zadania testowe/Statystyka/Średnia
Średnia arytmetyczna wszystkich wyrazów 100-wyrazowego ciągu arytmetycznego 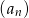 jest równa 37, a różnica tego ciągu jest równa
jest równa 37, a różnica tego ciągu jest równa 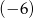 . Pierwszy wyraz ciągu
. Pierwszy wyraz ciągu 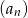 jest równy
jest równy
A) 594 B) 520 C) 260 D) 334
W pięcioosobowej grupie średnia wieku trzech kobiet wynosi 26 lat, a średnia wieku dwóch mężczyzn 36 lat. Średnia wieku wszystkich osób jest równa
A) 33 lata B) 32 lata C) 31 lat D) 30 lat
W dziewięcioosobowej grupie średnia wieku czterech kobiet wynosi 22 lata, a średnia wieku pięciu mężczyzn 40 lat. Średnia wieku wszystkich osób jest równa
A) 33 lata B) 32 lata C) 31 lata D) 30 lat
W siedmioosobowej grupie średnia wieku trzech kobiet wynosi 29 lat, a średnia wieku czterech mężczyzn 36 lat. Średnia wieku wszystkich osób jest równa
A) 33 lata B) 32 lata C) 31 lata D) 30 lat
W poniższej tabeli zebrano zarobki wszystkich pracowników pewnej firmy handlowej.
| Imię pracownika | Zarobki |
| Kamila, Krzysztof, Stefan | 2800 zł |
| Zofia, Łukasz | 3000 zł |
| Ela, Marta | 3200 zł |
| Henryk | 3600 zł. |
Jaka jest średnia zarobków pracowników tej firmy?
A) 3050 zł B) 3150 zł C) 3200 zł D) 3250 zł
Ciąg 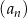 jes określony wzorem
jes określony wzorem 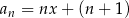 dla
dla 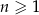 i pewnej liczby rzeczywistej
i pewnej liczby rzeczywistej  . Średnia arytmetyczna pierwszych ośmiu wyrazów tego ciągu jest równa 19. Wtedy
. Średnia arytmetyczna pierwszych ośmiu wyrazów tego ciągu jest równa 19. Wtedy  jest równe
jest równe
A) 3 B) 1,5 C) 27 D) 6
Uczniowie pewnej klasy zostali poproszeni o odpowiedź na pytanie: „Ile osób liczy twoja rodzina?” Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba uczniów |
| 3 | 6 |
| 4 | 12 |
| x | 2 |
Średnia liczba osób w rodzinie dla uczniów tej klasy jest równa 4. Wtedy liczba x jest równa
A) 3 B) 4 C) 5 D) 7
Grupa przypadkowych przechodniów została poproszona o odpowiedź na pytanie: „ile osób liczy Państwa rodzina?”. Wyniki przedstawiono w tabeli:
| Liczba osób w rodzinie | Liczba odpowiedzi |
| 2 | 6 |
| x | 12 |
| 5 | 2 |
Średnia liczba osób w rodzinie dla pytanych osób jest równa 3,5. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 1 D) 7
Pan Adam kupił 12 opakowań gwoździ i 6 opakowań wkrętów. Jedno opakowanie gwoździ kosztowało 4,5 zł, a średnia arytmetyczna cen wszystkich zakupionych produktów była równa 6 zł. Ile Pan Adam zapłacił za 6 opakowań wkrętów?
A) 6 zł B) 27 zł C) 48 zł D) 54 zł
Średnia arytmetyczna zestawu danych: 2, 4, 7, 8,  jest równa
jest równa  , natomiast średnia arytmetyczna zestawu danych: 2, 4, 7, 8,
, natomiast średnia arytmetyczna zestawu danych: 2, 4, 7, 8,  ,
, 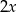 jest równa
jest równa 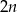 . Wynika stąd, że
. Wynika stąd, że
A) 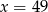 B)
B) 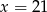 C)
C) 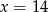 D)
D) 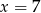
Średnia arytmetyczna zestawu danych: 1, 3, 6, 7,  jest równa
jest równa  , natomiast średnia arytmetyczna zestawu danych: 1, 3, 7, 7,
, natomiast średnia arytmetyczna zestawu danych: 1, 3, 7, 7,  ,
, 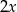 jest równa
jest równa 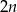 . Wynika stąd, że
. Wynika stąd, że
A) 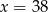 B)
B) 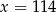 C)
C) 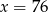 D)
D) 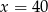
Średnia arytmetyczna zestawu danych: 7, 12, 8, 6,  ,
, 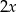 jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,
jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,  ,
,  ,
, 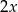 . Wynika stąd, że
. Wynika stąd, że
A) 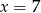 B)
B) 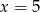 C)
C) 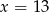 D)
D) 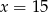
Rzucono 100 razy sześcienną kostką do gry. Średnia arytmetyczna liczb oczek w pierwszych 40 rzutach była równa 3,75, a średnia arytmetyczna liczb oczek w kolejnych 60 rzutach była równa 4,25. Średnia arytmetyczna liczb oczek w 100 rzutach jest
A) mniejsza od 4 B) równa 4 C) równa 4,05 D) większa od 4,05
Pewna firma postanowiła przeprowadzić badanie jakości pewnego produktu. W tym celu przeprowadziła testy w kategoriach jakość wykonania, wygląd i ergonomia, a następnie przyznano za każdą z tych cech punkty w skali od 1 do 6. Każdej badanej kategorii nadano wagę. Poniższa tabela przedstawia punktację uzyskaną przez produkt "Najlepszy" oraz wagi przypisane badanym kategoriom. Końcowa ocena jest średnią ważoną liczby uzyskanych punktów. Jaką ocenę uzyskał produkt "Najlepszy"?
| Kategoria | Waga | Liczba punktów |
| jakość wykonania | 20 | 6 |
| wygląd | 40 | 3 |
| ergonomia | 40 | 4 |
A) 4,2 B) 4 C) 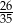 D) 0,12
D) 0,12
Pewna firma postanowiła przeprowadzić badanie jakości pewnego produktu. W tym celu przeprowadziła testy w kategoriach jakość wykonania, wygląd i ergonomia, a następnie przyznano za każdą z tych cech punkty w skali od 1 do 6. Każdej badanej kategorii nadano wagę. Poniższa tabela przedstawia punktację uzyskaną przez produkt "Najlepszy" oraz wagi przypisane badanym kategoriom. Końcowa ocena jest średnią ważoną liczby uzyskanych punktów. Jaką ocenę uzyskał produkt "Najlepszy"?
| Kategoria | Waga | Liczba punktów |
| jakość wykonania | 45 | 6 |
| wygląd | 25 | 2 |
| ergonomia | 30 | 5 |
A) 4,2 B) 4 C) 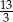 D) 4,7
D) 4,7
Pewna firma postanowiła przeprowadzić badanie jakości pewnego produktu. W tym celu przeprowadziła testy w kategoriach jakość wykonania, wygląd i ergonomia, a następnie przyznano za każdą z tych cech punkty w skali od 1 do 6. Każdej badanej kategorii nadano wagę. Poniższa tabela przedstawia punktację uzyskaną przez produkt "Najlepszy" oraz wagi przypisane badanym kategoriom. Końcowa ocena jest średnią ważoną liczby uzyskanych punktów. Jaką ocenę uzyskał produkt "Najlepszy"?
| Kategoria | Waga | Liczba punktów |
| jakość wykonania | 15 | 3 |
| wygląd | 35 | 5 |
| ergonomia | 50 | 4 |
A) 4,2 B) 4 C) 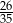 D) 0,12
D) 0,12
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 1 | 4 | 3 | 5 | 4 | 3 |
Średnia liczba oczek otrzymana w jednym rzucie jest równa.
A) 4 B) 3,8 C) 3,5 D) 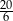
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 5 | 3 | 4 | 1 | 5 | 2 |
Średnia liczba oczek otrzymana w jednym rzucie jest równa.
A) 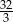 B) 3,5 C) 3,2 D)
B) 3,5 C) 3,2 D) 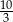
Ania otrzymała z pięciu sprawdzianów z matematyki następujące oceny: 5, 2, 3, 2, 5. Po kolejnych dwóch sprawdzianach średnia ocen Ani ze wszystkich sprawdzianów wyniosła 4. Jakie oceny mogła otrzymać Ania z ostatnich dwóch sprawdzianów?
A) 4 i 5 B) 5 i 5 C) 6 i 6 D) 5 i 6
Tomek otrzymał z sześciu sprawdzianów z matematyki następujące oceny: 5, 4, 2, 3, 2, 3. Po kolejnych dwóch sprawdzianach średnia ocen Tomka ze wszystkich sprawdzianów wyniosła 3,5. Jakie oceny mógł otrzymać Tomek z ostatnich dwóch sprawdzianów?
A) 4 i 4 B) 4 i 5 C) 3 i 4 D) 5 i 3
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
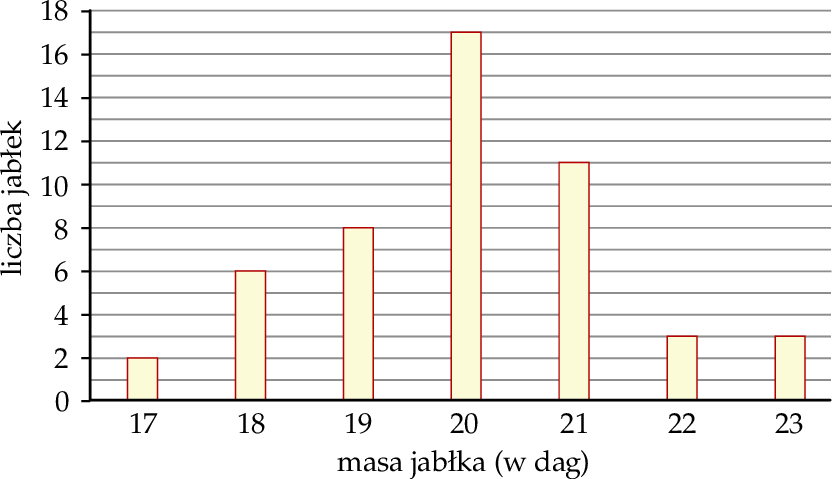
Średnia masy 50 zważonych jabłek z pobranej próby kontrolnej jest
| A) mniejsza niż 21 dag, | B) większa niż 21 dag, |
ponieważ
| 1) | większość jabłek waży 20 dag. |
| 2) | suma iloczynów masy i liczby jabłek o takiej masie jest mniejsza niż 1050 dag. |
| 3) | większość jabłek waży co najmniej 20 dag. |
Średnia arytmetyczna zestawu pewnych stu liczb całkowitych dodatnich jest równa  . Każdą z liczb tego zestawu zwiększamy o 4, w wyniku czego otrzymujemy nowy zestaw stu liczb. Średnia arytmetyczna nowego zestawu stu liczb jest równa
. Każdą z liczb tego zestawu zwiększamy o 4, w wyniku czego otrzymujemy nowy zestaw stu liczb. Średnia arytmetyczna nowego zestawu stu liczb jest równa
A) 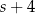 B)
B) 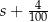 C)
C) 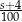 D)
D) 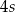
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
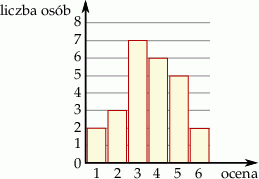
Średnia ocen ze sprawdzianu jest równa
A) 4 B) 3,6 C) 3,5 D) 3
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
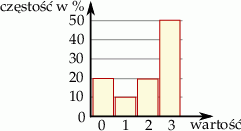
A) 2 B) 1 C) 1,5 D) 1,8
Firma 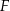 zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy 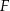 , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
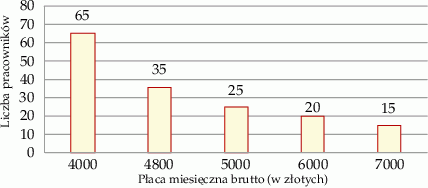
Średnia miesięczna płaca brutto w firmie 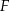 jest równa
jest równa
A) 4 862,5 zł B) 4 800,00 zł C) 5 360,00 zł D) 4 593,75 zł
Na diagramie przedstawiono wyniki sprawdzianu z matematyki w pewnej klasie maturalnej. Na osi poziomej podano oceny, które uzyskali uczniowie tej klasy, a na osi pionowej podano liczbę uczniów, którzy otrzymali daną ocenę.
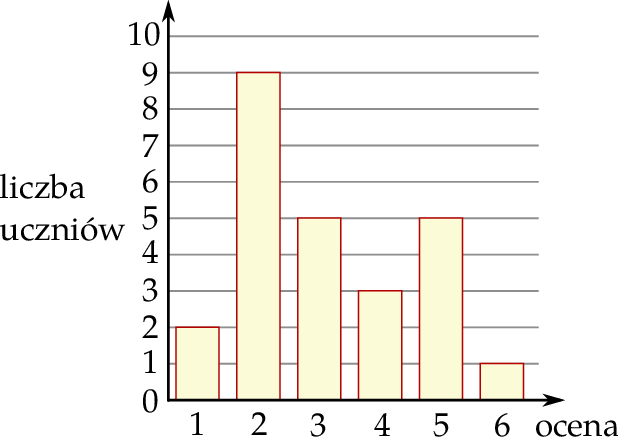
Średnia arytmetyczna ocen uzyskanych z tego sprawdzianu przez uczniów tej klasy jest równa
A) 3 B) 3,12 C) 3,5 D) 4,1(6)
Przeprowadzono badanie dotyczące liczby samochodów osobowych w rodzinie. Wyniki przedstawia poniższy diagram
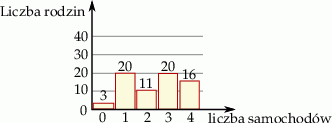
Wartość średnia liczby samochodów w rodzinie wynosi
A) 2 B) 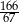 C)
C) 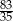 D) 3
D) 3
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
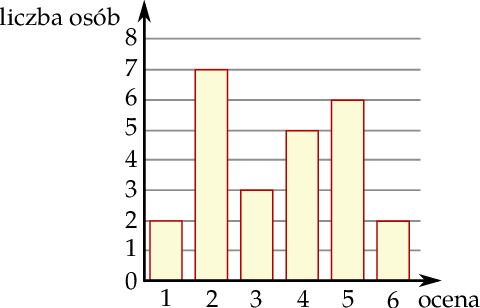
Średnia ocen ze sprawdzianu jest równa
A) 3,48 B) 4 C) 3,5 D) 3
Firma 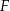 zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy
zatrudnia 160 osób. Rozkład płac brutto pracowników tej firmy przedstawia poniższy diagram. Na osi poziomej podano – wyrażoną w złotych – miesięczną płacę brutto, a na osi pionowej podano liczbę pracowników firmy 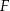 , którzy otrzymują płacę miesięczną w danej wysokości.
, którzy otrzymują płacę miesięczną w danej wysokości.
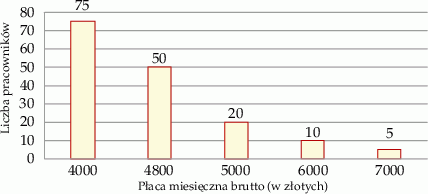
Średnia miesięczna płaca brutto w firmie 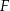 jest równa
jest równa
A) 4 593,75 zł B) 4 800,00 zł C) 5 360,00 zł D) 2 399,33 zł
Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2024 roku.
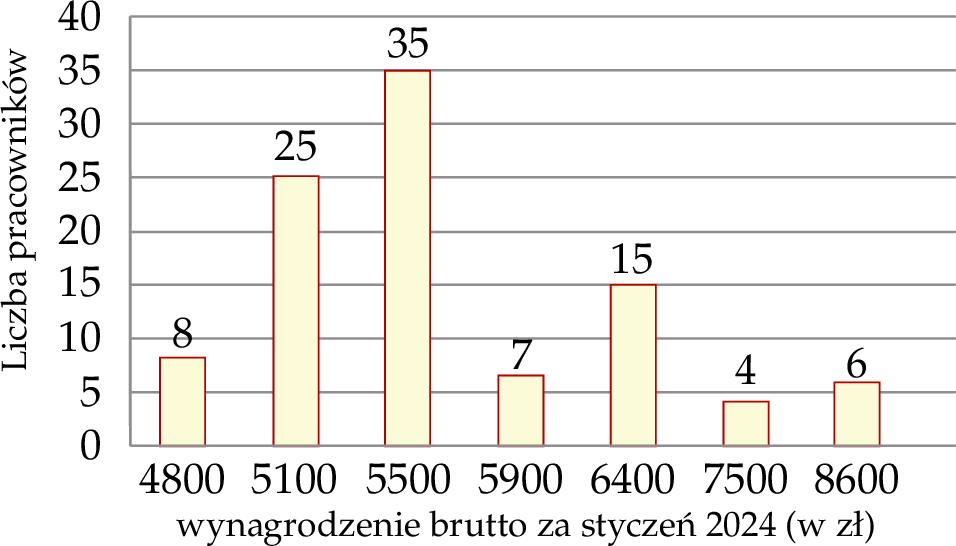
Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2024 roku jest równa
A) 7 300 zł B) 5 280 zł C) 6 257 zł D) 5 773 zł
Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2023 roku.
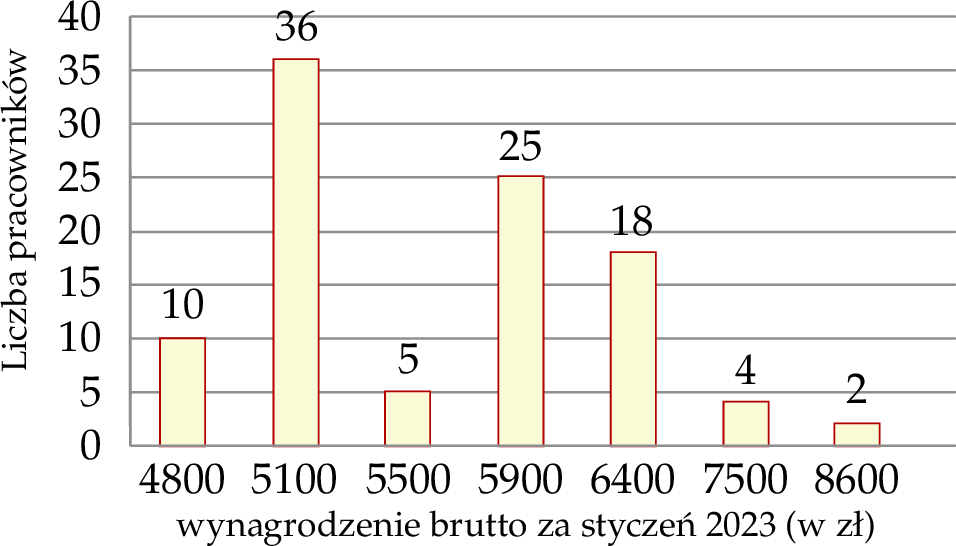
Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2023 roku jest równa
A) 5 690 zł B) 5 280 zł C) 6 257 zł D) 5 900 zł
Wyniki sprawdzianu z matematyki są przedstawione na diagramie
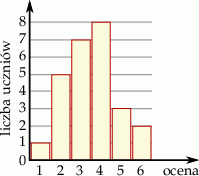
Średnia ocen uzyskanych przez uczniów z tego sprawdzianu jest równa
A) 2 B) 3 C) 3,5 D) 4
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
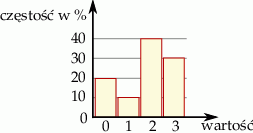
A) 1 B) 1,2 C) 1,5 D) 1,8
Średnia danych przestawionych na wykresie słupkowym jest równa:
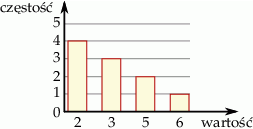
A) 8,25 B) 4 C) 3,3 D) 0,625
Średnia arytmetyczna danych przedstawionych na diagramie częstości jest równa
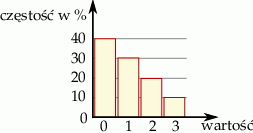
A) 1 B) 1,2 C) 1,5 D) 1,8
Na diagramie poniżej znajdują się wyniki z matematyki uczniów klasy IIIA na pierwszy semestr.
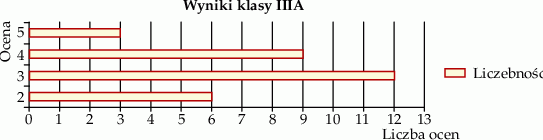
Średnia ocen z matematyki w tej klasie jest równa:
A) 3 B) 3,3 C) 3,5 D) 3,8
Janek w pierwszym semestrze otrzymał następujące oceny z matematyki: z prac klasowych 2, 3, 3, 4, z kartkówek 5, 5, 4, 4, 5, 5, z odpowiedzi ustnych 2, 3, 4. Oceny z prac klasowych mają wagę 0,5, z kartkówek 0,3, z odpowiedzi ustnych 0,2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Janka w pierwszym semestrze jest równa
A) 3,68 B) 3,58 C) 3,25 D) 1,23
Kasia w pierwszym semestrze otrzymała następujące oceny z matematyki: z prac klasowych 3, 4, 4, 2, z kartkówek 5, 4, 4, 3, 5, z zadań domowych 3, 4, 5. Oceny z prac klasowych mają wagę 5, z kartkówek 3, z zadania domowego 2. Średnia ważona (zaokrąglona do dwóch miejsc po przecinku) ocen z matematyki Kasi w pierwszym semestrze jest równa
A) 3,71 B) 4,6 C) 13,7 D) 11,41
Średnia arytmetyczna pięciu liczb: 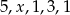 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 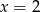 B)
B) 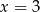 C)
C) 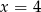 D)
D) 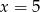
Średnia arytmetyczna sześciu liczb: 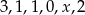 jest równa 2. Wtedy liczba
jest równa 2. Wtedy liczba  jest równa
jest równa
A) 3 B) 4 C) 5 D) 6
Dla jakiej wartości liczbowej  średnia arytmetyczna liczb:
średnia arytmetyczna liczb: 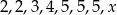 jest równa 4?
jest równa 4?
A) 6 B) 5 C) 4 D) 3
Średnia arytmetyczna zestawu sześciu liczb: 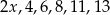 , jest równa 5. Wynika stąd, że
, jest równa 5. Wynika stąd, że
A) 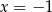 B)
B) 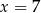 C)
C) 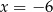 D)
D) 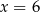
Średnia arytmetyczna zestawu danych: 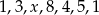 wynosi 4. Wynika z tego, że:
wynosi 4. Wynika z tego, że:
A) 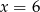 B)
B) 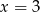 C)
C) 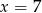 D)
D) 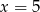
Średnia arytmetyczna pięciu liczb: 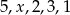 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 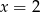 B)
B) 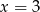 C)
C) 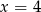 D)
D) 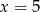
Średnia arytmetyczna ośmiu liczb: 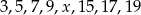 jest równa 11. Wtedy
jest równa 11. Wtedy
A) 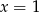 B)
B) 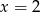 C)
C) 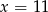 D)
D) 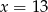
Średnia arytmetyczna zestawu danych: 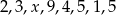 wynosi 4,5. Wynika z tego, że:
wynosi 4,5. Wynika z tego, że:
A) 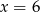 B)
B) 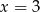 C)
C) 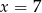 D)
D) 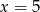
Średnia arytmetyczna pięciu liczb: 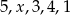 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 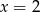 B)
B) 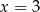 C)
C) 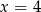 D)
D) 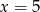
Średnia arytmetyczna siedmiu liczb: 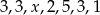 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 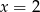 B)
B) 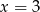 C)
C) 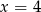 D)
D) 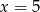
Średnia arytmetyczna liczb 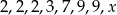 jest równa 4,5. Liczba
jest równa 4,5. Liczba  jest równa
jest równa
A) 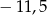 B) 1 C) 1,5 D) 2
B) 1 C) 1,5 D) 2
Średnia arytmetyczna dziesięciu liczb 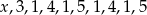 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 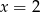 B)
B) 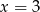 C)
C) 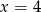 D)
D) 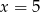
Średnia arytmetyczna liczb: 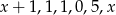 jest równa
jest równa  . Wtedy liczba
. Wtedy liczba  jest równa
jest równa
A)  B) 2 C)
B) 2 C)  D)
D) 
Średnia arytmetyczna zestawu danych: 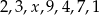 wynosi
wynosi 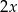 . Wynika z tego, że:
. Wynika z tego, że:
A) 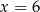 B)
B) 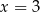 C)
C) 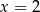 D)
D) 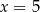
Średnia arytmetyczna dziesięciu liczb 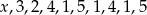 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 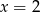 B)
B) 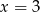 C)
C) 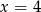 D)
D) 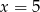
Średnia arytmetyczna pięciu liczb: 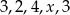 jest równa 3,2. Wtedy
jest równa 3,2. Wtedy
A) 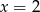 B)
B) 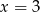 C)
C) 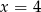 D)
D) 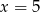
Średnia arytmetyczna ocen Jacka jest równa 3,75, a średnia ocen Karola (liczona z dokładnie tej samej liczby ocen) jest równa 4,25. Średnia ocen obu chłopców jest równa
A) 3,95 B) 4,5 C) 4,0 D) 4,15
Średnia arytmetyczna ocen Zosi jest równa 2,8, a średnia ocen Basi (liczona z dokładnie tej samej liczby ocen) jest równa 4,4. Średnia ocen obu dziewcząt jest równa
A) 3,6 B) 4,0 C) 3,8 D) 4,15
Średnia arytmetyczna cen sześciu akcji na giełdzie jest równa 500 zł. Za pięć z tych akcji zapłacono 2300 zł. Cena szóstej akcji jest równa
A) 400 zł B) 500 zł C) 600 zł D) 700 zł
Średnia arytmetyczna cen dziewięciu akcji na giełdzie jest równa 680 zł. Za osiem z tych akcji zapłacono 5500 zł. Cena dziewiątej akcji jest równa
A) 660 zł B) 580 zł C) 620 zł D) 760 zł
Średnia cena sześciu kartonów mleka po 3,2 zł za karton i dwóch identycznych pojemników śmietany wynosi 2,85 zł. Cena jednego pojemnika śmietany jest równa
A) 1,8 zł B) 3,6 zł C) 2 zł D) 2,4 zł
Państwo Nowakowie mają trzy córki i jednego syna. Średnia wieku wszystkich dzieci państwa Nowaków jest równa 10 lat, a średnia wieku wszystkich córek jest równa 8 lat. Ile lat ma syn państwa Nowaków?
A) 9 B) 11 C) 12 D) 16
Średnia arytmetyczna cen ośmiu akcji na giełdzie jest równa 600 zł. Za siedem z tych akcji zapłacono 4200 zł. Cena ósmej akcji jest równa
A) 400 zł B) 500 zł C) 600 zł D) 700 zł
Kamil ma trzy siostry i jednego brata bliźniaka. Średnia wieku wszystkich dzieci w tej rodzinie jest równa 10,2 roku, a średnia wieku samych dziewcząt jest równa 7 lat. Ile lat ma Kamil?
A) 30 B) 17 C) 15 D) 21
Kasia kupiła cztery ołówki i długopis. Średnia arytmetyczna cen tych pięciu artykułów była równa 1,8 zł. Ołówki kosztowały łącznie 6 zł. Ile kosztował długopis?
A) 2,7 zł B) 1,5 zł C) 2 zł D) 3 zł
Ala kupiła trzy zeszyty i blok rysunkowy. Średnia arytmetyczna cen tych czterech artykułów była równa 6 zł. Zeszyty kosztowały łącznie 15 zł. Ile kosztował blok rysunkowy?
A) 4 zł B) 5 zł C) 8 zł D) 9 zł

