Równanie 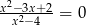 ma:
ma:
A) 2 pierwiastki B) 3 pierwiastki C) 1 pierwiastek D) 4 pierwiastki
/Szkoła średnia/Zadania testowe/Równania/Wymierne
Wszystkimi rozwiązaniami równania wymiernego 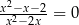 są
są
A) 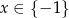 B)
B) 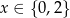 C)
C) 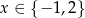 D)
D) 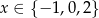
Rozwiązaniami równania 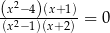 są liczby
są liczby
A) 2 B) 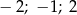 C)
C) 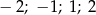 D)
D) 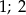
Równanie
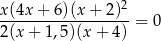
ma w zbiorze liczb rzeczywistych
A) dokładnie jedno rozwiązanie: 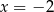 .
.
B) dokładnie dwa rozwiązania: 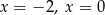 .
.
C) dokładnie trzy rozwiązania: 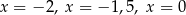 .
.
D) dokładnie cztery rozwiązania: 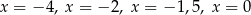 .
.
Równanie
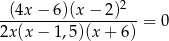
ma w zbiorze liczb rzeczywistych
A) dokładnie jedno rozwiązanie: 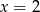 .
.
B) dokładnie dwa rozwiązania: 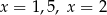 .
.
C) dokładnie trzy rozwiązania: 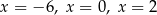 .
.
D) dokładnie cztery rozwiązania: 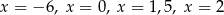 .
.
Liczba rozwiązań równania 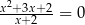 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Rozwiązaniem równania 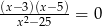 jest liczba:
jest liczba:
A) 3 B) -5 C) 5 D) 0
Rozwiązaniem równania 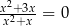 jest liczba
jest liczba
A) 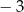 B) 0 C) 3 D) 9
B) 0 C) 3 D) 9
Rozwiązaniem równania 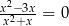 jest liczba
jest liczba
A) 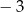 B) 0 C) 3 D) 9
B) 0 C) 3 D) 9
Równanie 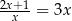
A) ma dwa rozwiązania: 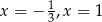 B) ma dwa rozwiązania:
B) ma dwa rozwiązania: 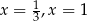
C) nie ma żadnego rozwiązania D) ma tylko jedno rozwiązanie 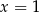
Równanie 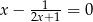
A) ma dokładnie dwa rozwiązania rzeczywiste.
B) ma dokładnie trzy rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań.
Równanie 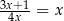
A) ma dwa rozwiązania: 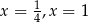 B) ma dwa rozwiązania:
B) ma dwa rozwiązania: 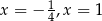
C) ma dwa rozwiązania: 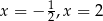 D) ma tylko jedno rozwiązanie
D) ma tylko jedno rozwiązanie 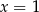
Równanie 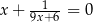
A) ma dokładnie dwa rozwiązania rzeczywiste.
B) ma dokładnie trzy rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań.
Rozwiązaniem równania 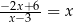 jest
jest
A) 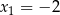 B)
B) 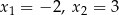 C)
C) 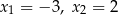 D)
D) 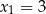
Liczba rozwiązań równania 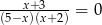 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Równanie 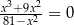 ma w zbiorze liczb rzeczywistych dokładnie
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Równanie 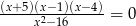
A) nie ma pierwiastków
B) ma jeden pierwiastek
C) ma dwa pierwiastki
D) ma trzy pierwiastki
Liczba rozwiązań równania 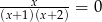 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Równanie 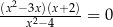 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Równanie 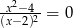
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie trzy rozwiązania
Równanie 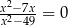 ma w zbiorze liczb rzeczywistych dokładnie
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania.
C) trzy rozwiązania. D) cztery rozwiązania.
Równanie 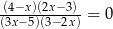 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Wskaż liczbę rozwiązań równania 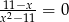 .
.
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 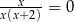 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba miejsc zerowych funkcji 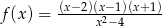 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 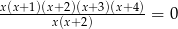 jest równa
jest równa
A) 6 B) 5 C) 4 D) 3
Równanie 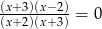 ma
ma
A) dokładnie jedno rozwiązanie
B) dokładnie dwa rozwiązania
C) dokładnie trzy rozwiązania
D) dokładnie cztery rozwiązania
Równanie 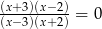 ma
ma
A) dokładnie jedno rozwiązanie
B) dokładnie dwa rozwiązania
C) dokładnie trzy rozwiązania
D) dokładnie cztery rozwiązania
Równanie 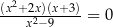 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) cztery rozwiązania. B) trzy rozwiązania.
C) dwa rozwiązania. D) jedno rozwiązanie.
Równanie 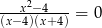
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Równanie 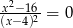
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania
D) ma dokładnie cztery rozwiązania.
Równanie 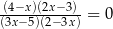 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania
Rozwiązaniem równania 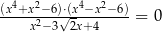 nie jest liczba
nie jest liczba
A) 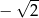 B)
B) 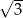 C)
C) 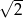 D)
D) 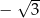
Rozwiązaniem równania 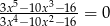 jest liczba
jest liczba
A) 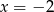 B)
B) 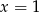 C)
C) 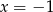 D)
D) 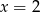
Równanie
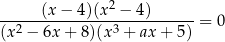
z niewiadomą  nie ma rozwiązań rzeczywistych. Liczba
nie ma rozwiązań rzeczywistych. Liczba  jest więc równa
jest więc równa
A) 6,5 B) 4 C) 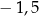 D)
D) 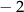
Równanie 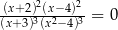
A) ma cztery różne rozwiązania: 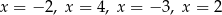 .
.
B) ma trzy różne rozwiązania: 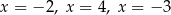 .
.
C) ma dwa różne rozwiązania: 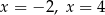 .
.
D) ma jedno rozwiązanie: 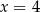 .
.
Równanie 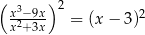
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Jednym z rozwiązań równania 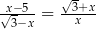 jest
jest
A) 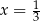 B)
B) 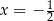 C)
C) 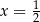 D)
D) 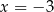
Jednym z rozwiązań równania 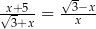 jest
jest
A) 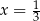 B)
B) 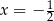 C)
C) 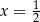 D)
D) 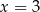
Wskaż równanie, którego rozwiązaniami są liczby 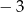 oraz 5.
oraz 5.
A) 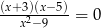 B)
B) 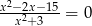 C)
C) 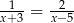 D)
D) 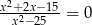
Wskaż równanie, którego rozwiązaniami są liczby 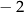 oraz 3.
oraz 3.
A) 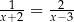 B)
B) 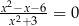 C)
C) 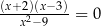 D)
D) 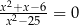
Ile rozwiązań posiada równanie 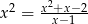 ?
?
A) 0 B) 1 C) 2 D) 3
Rozwiązaniami równania 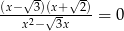 jest
jest
A) tylko 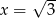 B)
B) 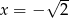 i
i 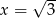 C) tylko
C) tylko 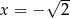 D)
D) 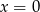 i
i 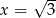
Rozwiązaniem równania 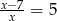 , gdzie
, gdzie 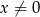 , jest liczba należąca do przedziału
, jest liczba należąca do przedziału
A) 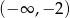 B)
B) 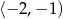 C)
C) 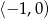 D)
D) 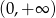
Rozwiązaniem równania 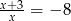 , gdzie
, gdzie 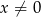 , jest liczba należąca do przedziału
, jest liczba należąca do przedziału
A) 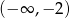 B)
B) 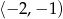 C)
C) 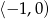 D)
D) 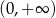
Rozwiązaniem równania 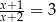 , gdzie
, gdzie 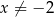 jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 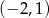 B)
B) 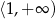 C)
C) 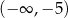 D)
D) 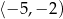
Rozwiązaniem równania 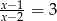 , gdzie
, gdzie  jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 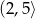 B)
B) 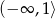 C)
C) 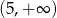 D)
D) 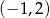
Równanie wymierne 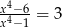 , gdzie
, gdzie 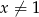 i
i 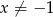 ,
,
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma dokładnie cztery rozwiązania rzeczywiste.
Jednym z rozwiązań równania 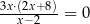 jest liczba
jest liczba
A) 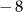 B)
B) 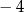 C) 2 D) 3
C) 2 D) 3
Równanie 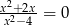
A) ma trzy rozwiązania: 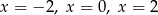
B) ma dwa rozwiązania: 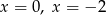
C) ma dwa rozwiązania: 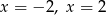
D) ma jedno rozwiązanie: 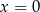
Równanie 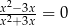
A) ma trzy rozwiązania: 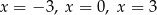
B) ma jedno rozwiązanie: 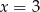
C) ma dwa rozwiązania: 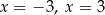
D) ma dwa rozwiązania: 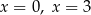
Równanie 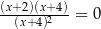 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 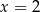 B) jedno rozwiązanie:
B) jedno rozwiązanie: 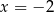
C) dwa rozwiązania: 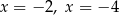 D) dwa rozwiązania:
D) dwa rozwiązania: 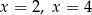
Równanie
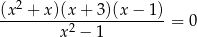
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 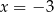
B) dwa rozwiązania: 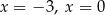
C) trzy rozwiązania: 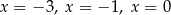
D) cztery rozwiązania: 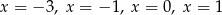
Równanie 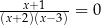 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie: 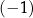 .
.
C) ma dokładnie dwa rozwiązania: 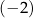 oraz 3.
oraz 3.
D) ma dokładnie trzy rozwiązania: 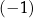 ,
, 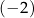 oraz 3.
oraz 3.
Równanie 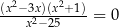 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Równanie 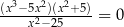 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Funkcja 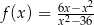
A) ma jedno miejsce zerowe 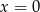
B) ma dwa miejsca zerowe: 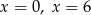
C) ma dwa miejsce zerowe: 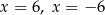
D) ma trzy miejsca zerowe: 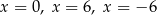
Równanie 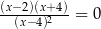 ma dokładnie
ma dokładnie
A) jedno rozwiązanie: 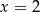 B) jedno rozwiązanie:
B) jedno rozwiązanie: 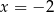
C) dwa rozwiązania: 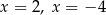 D) dwa rozwiązania:
D) dwa rozwiązania: 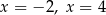
Równanie
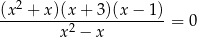
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 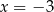
B) dwa rozwiązania: 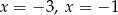
C) trzy rozwiązania: 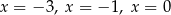
D) cztery rozwiązania: 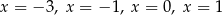
Równanie
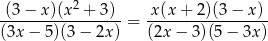
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie B) dwa rozwiązania
C) trzy rozwiązania D) cztery rozwiązania

