Równość 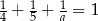 jest prawdziwa dla
jest prawdziwa dla
A) 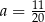 B)
B) 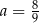 C)
C) 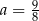 D)
D) 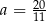
/Szkoła średnia/Zadania testowe/Równania/Wymierne
Równość 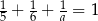 jest prawdziwa dla
jest prawdziwa dla
A) 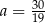 B)
B) 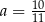 C)
C) 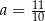 D)
D) 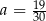
Jednym z rozwiązań równania 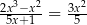 jest liczba
jest liczba
A) 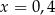 B)
B) 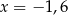 C)
C) 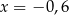 D)
D) 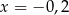
Równanie 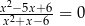
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma dokładnie trzy rozwiązania
Liczba rozwiązań równania 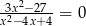 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 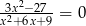 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba rozwiązań równania 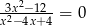 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Równanie 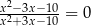
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma dokładnie trzy rozwiązania
Równanie 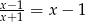
A) ma dokładnie jedno rozwiązanie: 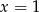 .
.
B) ma dokładnie jedno rozwiązanie: 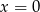 .
.
C) ma dokładnie jedno rozwiązanie: 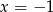 .
.
D) ma dokładnie dwa rozwiązania: 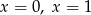 .
.
Równanie 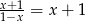
A) ma dokładnie jedno rozwiązanie: 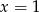 .
.
B) ma dokładnie dwa rozwiązania: 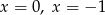 .
.
C) ma dokładnie jedno rozwiązanie: 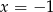 .
.
D) ma dokładnie jedno rozwiązanie: 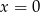 .
.
Równanie 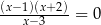
A) ma trzy różne rozwiązania: 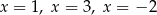 .
.
B) ma trzy różne rozwiązania: 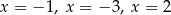 .
.
C) ma dwa różne rozwiązania: 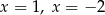 .
.
D) ma dwa różne rozwiązania: 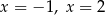 .
.
Równanie 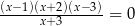
A) ma trzy różne rozwiązania: 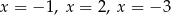 .
.
B) ma trzy różne rozwiązania: 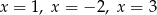 .
.
C) ma dwa różne rozwiązania: 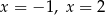 .
.
D) ma dwa różne rozwiązania: 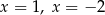 .
.
Równanie 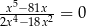
A) ma dwa rozwiązania B) ma trzy rozwiązania
C) nie ma rozwiązań D) ma jedno rozwiązanie
Równanie 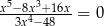
A) ma dwa rozwiązania B) ma trzy rozwiązania
C) nie ma rozwiązań D) ma jedno rozwiązanie
Równanie 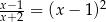
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie trzy rozwiązania.
Równanie 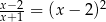
A) ma dokładnie trzy rozwiązania. B) ma dokładnie dwa rozwiązania.
C) ma dokładnie jedno rozwiązanie. D) nie ma rozwiązań.
Równanie 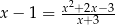
A) spełnia każda liczba rzeczywista B) jest sprzeczne
C) ma mniej niż 5 rozwiązań D) ma rozwiązania ujemne
Dla 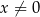 równanie
równanie 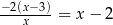
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dwa różne rozwiązania D) ma trzy różne rozwiązania
Rozwiązaniem równania 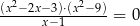 nie jest liczba
nie jest liczba
A) 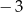 B)
B) 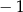 C) 1 D) 3
C) 1 D) 3
Rozwiązaniem równania 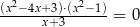 nie jest liczba
nie jest liczba
A) 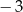 B)
B) 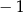 C) 1 D) 3
C) 1 D) 3
Liczba rozwiązań równania 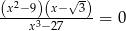 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba rozwiązań równania 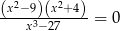 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba rozwiązań równania 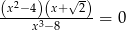 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Równość 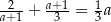 jest prawdziwa dla liczby wymiernej
jest prawdziwa dla liczby wymiernej
A) 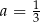 B)
B) 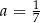 C)
C) 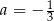 D)
D) 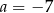
Rozwiązaniem równania 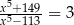 , gdzie
, gdzie 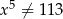 jest liczba należąca do przedziału
jest liczba należąca do przedziału
A) 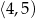 B)
B) 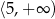 C)
C) 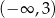 D)
D) 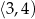
Równanie wymierne 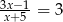 , gdzie
, gdzie 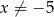 ,
,
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma dokładnie trzy rozwiązania rzeczywiste.
Równanie wymierne 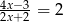 , gdzie
, gdzie 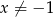 ,
,
A) ma dokładnie trzy rozwiązania rzeczywiste.
B) ma dokładnie dwa rozwiązania rzeczywiste.
C) ma dokładnie jedno rozwiązanie rzeczywiste.
D) nie ma rozwiązań rzeczywistych.
Równanie 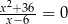
A) nie ma rozwiązań. B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania. D) ma dokładnie trzy rozwiązania.
Równanie
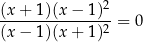
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie 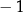 .
.
C) ma dokładnie jedno rozwiązanie 1.
D) ma dokładnie dwa rozwiązania 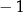 oraz 1.
oraz 1.
Równanie
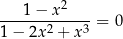
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie 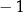 .
.
C) ma dokładnie jedno rozwiązanie 1.
D) ma dokładnie dwa rozwiązania 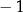 oraz 1.
oraz 1.
Równanie
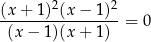
w zbiorze liczb rzeczywistych
A) nie ma rozwiązania.
B) ma dokładnie jedno rozwiązanie 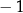 .
.
C) ma dokładnie jedno rozwiązanie 1.
D) ma dokładnie dwa rozwiązania 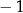 oraz 1.
oraz 1.
Równanie 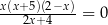 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) dwa rozwiązania: 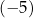 oraz 2.
oraz 2.
B) dwa rozwiązania: 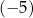 oraz 0.
oraz 0.
C) trzy rozwiązania: 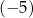 , 0 oraz 2.
, 0 oraz 2.
D) cztery rozwiązania: 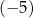 ,
, 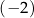 , 0 oraz 2.
, 0 oraz 2.
Rozwiązaniami równania 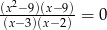 są liczby
są liczby
A) 2,-3,3,9 B) -3,3,9 C) -3,9 D) 2,3
Miejscami zerowymi funkcji wymiernej 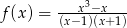 są liczby
są liczby
A) 0 B) 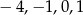 C)
C) 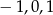 D)
D) 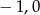
Miejscami zerowymi funkcji wymiernej 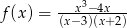 są liczby
są liczby
A) 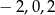 B)
B) 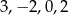 C)
C) 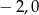 D)
D) 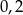
Rozwiązaniami równania 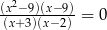 są liczby
są liczby
A) 2,-3,3,9 B) -3,3,9 C) -3,9 D) 3,9
Rozwiązaniami równania 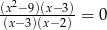 są liczby
są liczby
A) -3,2,3 B) -3 C) -3,2 D) -3,3
Miejscami zerowymi funkcji wymiernej 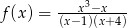 są liczby
są liczby
A) 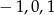 B)
B) 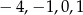 C) 0,1 D)
C) 0,1 D) 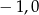
Rozwiązaniami równania 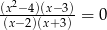 są liczby:
są liczby:
A) 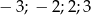 B)
B) 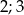 C)
C) 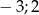 D)
D) 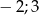
Rozwiązaniem równania 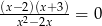 jest
jest
A) 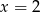 i
i 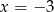 B) tylko
B) tylko 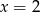 C) tylko
C) tylko 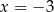 D)
D) 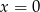 i
i 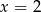
Iloczyn pierwiastków równania 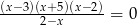 jest równy
jest równy
A) 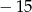 B) 15 C)
B) 15 C) 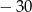 D) 30
D) 30
Iloczyn pierwiastków równania 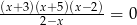 jest równy
jest równy
A) 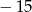 B) 15 C)
B) 15 C) 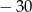 D) 30
D) 30
Rozwiązaniem równania 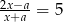 jest
jest 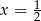 . Zatem
. Zatem
A) 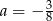 B)
B) 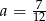 C)
C) 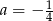 D)
D) 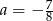
Równanie 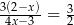 nie ma takiego samego rozwiązania, jak równanie
nie ma takiego samego rozwiązania, jak równanie
A) 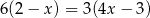 B)
B) 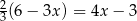
C) 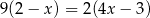 D)
D) 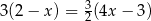
Równanie 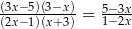 ma dwa rozwiązania. Są to liczby:
ma dwa rozwiązania. Są to liczby:
A) 3 i 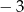 B) 3 i
B) 3 i 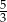 C) 0 i 3 D) 0 i
C) 0 i 3 D) 0 i 

