Na rysunku przedstawiony jest czworościan foremny 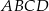 , którego objętość i pole powierzchni całkowitej są odpowiednio równe:
, którego objętość i pole powierzchni całkowitej są odpowiednio równe: 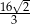 i
i 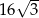 .
.
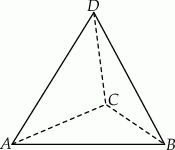
Promień okręgu wpisanego w ścianę 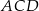 jest równy
jest równy
A) 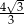 B)
B) 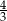 C)
C) 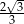 D)
D) 
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiony jest czworościan foremny 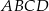 , którego objętość i pole powierzchni całkowitej są odpowiednio równe:
, którego objętość i pole powierzchni całkowitej są odpowiednio równe: 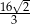 i
i 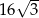 .
.

Promień okręgu wpisanego w ścianę 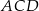 jest równy
jest równy
A) 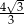 B)
B) 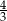 C)
C) 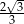 D)
D) 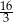
W ostrosłupie czworokątnym, w którym wszystkie krawędzie mają tę samą długość, kąt nachylenia krawędzi bocznej do płaszczyzny podstawy ma miarę
A) 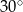 B)
B) 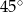 C)
C) 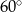 D)
D) 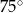
Podstawą ostrosłupa prawidłowego czworokątnego 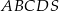 jest kwadrat
jest kwadrat 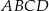 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
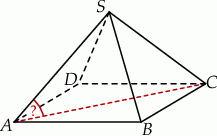
Miara kąta 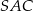 jest równa
jest równa
A) 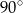 B)
B) 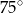 C)
C) 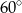 D)
D) 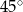
W ostrosłupie prawidłowym czworokątnym, w którym wszystkie krawędzie mają tę samą długość, kąt między wysokością ostrosłupa, a jego krawędzią boczną ma miarę
A) 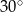 B)
B) 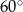 C)
C) 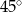 D)
D) 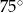
Na rysunku przedstawiony jest czworościan foremny 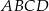 , którego objętość i pole powierzchni całkowitej są odpowiednio równe:
, którego objętość i pole powierzchni całkowitej są odpowiednio równe: 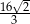 i
i 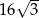 .
.
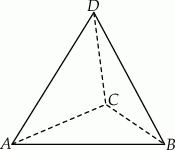
Wysokość czworościanu  jest równa
jest równa
A) 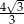 B)
B) 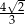 C)
C) 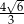 D)
D) 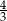
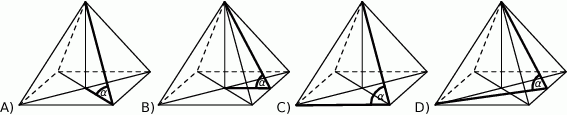
Kąt  nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
nachylenia ściany bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
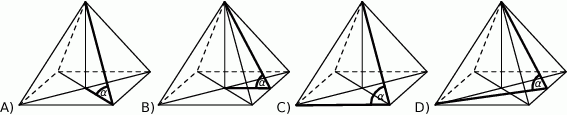
Kąt  nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
nachylenia krawędzi bocznej ostrosłupa prawidłowego czworokątnego do płaszczyzny podstawy zaznaczony jest na rysunku:
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 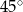 , a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
, a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
A) 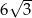 B) 9 C) 12 D)
B) 9 C) 12 D) 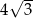
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa 11. Podstawą tego ostrosłupa jest
A) dziesięciokąt. B) jedenastokąt. C) dwunastokąt. D) trzynastokąt.
W pewnym ostrosłupie prawidłowym stosunek liczby 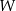 wszystkich wierzchołków do liczby
wszystkich wierzchołków do liczby 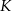 wszystkich krawędzi jest równy
wszystkich krawędzi jest równy 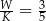 . Podstawą tego ostrosłupa jest
. Podstawą tego ostrosłupa jest
A) kwadrat. B) pięciokąt foremny.
C) sześciokąt foremny. D) siedmiokąt foremny.
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa 10. Podstawą tego ostrosłupa jest
A) dziesięciokąt. B) jedenastokąt. C) dwunastokąt. D) trzynastokąt.
W pewnym ostrosłupie prawidłowym stosunek liczby 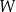 wszystkich wierzchołków do liczby
wszystkich wierzchołków do liczby 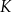 wszystkich krawędzi jest równy
wszystkich krawędzi jest równy 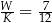 . Podstawą tego ostrosłupa jest
. Podstawą tego ostrosłupa jest
A) kwadrat. B) pięciokąt foremny.
C) sześciokąt foremny. D) siedmiokąt foremny.
Podstawą ostrosłupa jest kwadrat 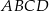 o boku długości 4. Krawędź boczna
o boku długości 4. Krawędź boczna 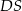 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
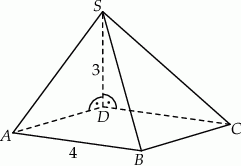
Pole ściany 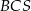 tego ostrosłupa jest równe
tego ostrosłupa jest równe
A) 20 B) 10 C) 16 D) 12
Podstawą ostrosłupa jest kwadrat 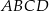 o boku długości 12. Krawędź boczna
o boku długości 12. Krawędź boczna 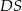 jest prostopadła do podstawy i ma długość 9 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 9 (zobacz rysunek).
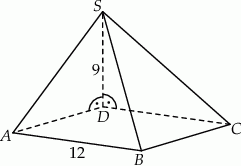
Pole ściany 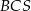 tego ostrosłupa jest równe
tego ostrosłupa jest równe
A) 180 B) 108 C) 54 D) 90
Wysokość ściany bocznej opuszczona na krawędź podstawy ostrosłupa prawidłowego trójkątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej do pola powierzchni podstawy tego ostrosłupa jest równy
A) 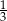 B)
B) 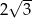 C)
C) 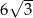 D) 9
D) 9
Suma długości wszystkich krawędzi czworościanu foremnego jest równa 12 cm. Pole powierzchni całkowitej tego czworościanu jest równe
A) 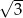 B)
B) 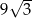 C)
C) 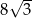 D)
D) 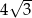
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość. Wynika stąd, że cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
A) 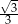 B)
B) 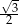 C)
C) 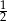 D)
D) 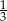
Na rysunku przedstawiono ostrosłup czworokątny 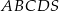 , którego podstawą jest kwadrat
, którego podstawą jest kwadrat 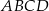 , i w którym krawędź
, i w którym krawędź 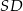 jest prostopadła do płaszczyzny podstawy (patrz rysunek).
jest prostopadła do płaszczyzny podstawy (patrz rysunek).
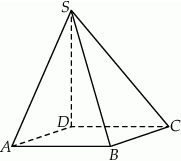
Które trzy punkty nie są wierzchołkami trójkąta prostokątnego?
A) 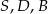 B)
B) 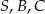 C)
C) 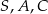 D)
D) 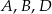
Liczba wszystkich ścian ostrosłupa prawidłowego jest równa 12. Liczba wszystkich wierzchołków tego ostrosłupa jest równa
A) 10 B) 11 C) 12 D) 13
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa 6, a objętość ostrosłupa wynosi 96. Stosunek wysokości ostrosłupa do długości krawędzi podstawy jest równy
A) 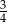 B)
B) 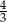 C)
C) 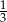 D)
D) 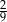
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa 9, a objętość ostrosłupa wynosi 81. Stosunek wysokości ostrosłupa do długości krawędzi podstawy jest równy
A) 3 B) 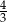 C)
C) 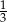 D)
D) 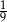
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest równa 8, a objętość ostrosłupa wynosi 128. Stosunek wysokości ostrosłupa do długości krawędzi podstawy jest równy
A) 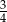 B)
B) 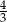 C)
C) 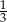 D)
D) 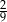
Dany jest ostrosłup prawidłowy czworokątny 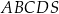 o podstawie
o podstawie 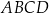 . Długość krawędzi podstawy tego ostrosłupa jest równa 4. Pole powierzchni całkowitej tego ostrosłupa jest równe 56. Wysokość ściany bocznej poprowadzona z wierzchołka
. Długość krawędzi podstawy tego ostrosłupa jest równa 4. Pole powierzchni całkowitej tego ostrosłupa jest równe 56. Wysokość ściany bocznej poprowadzona z wierzchołka 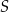 do krawędzi podstawy
do krawędzi podstawy 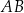 tego ostrosłupa jest równa
tego ostrosłupa jest równa
A) 3 B)  C)
C) 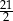 D) 5
D) 5
Dany jest ostrosłup, którego podstawą jest trójkąt równoboczny o boku 6. Jedna z krawędzi bocznych tego ostrosłupa ma długość 8 i jest prostopadła do płaszczyzny podstawy. Tangens kąta nachylenia tej ściany bocznej tego ostrosłupa, która jest trójkątem równoramiennym, do płaszczyzny podstawy jest równy
A) 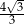 B)
B) 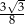 C)
C) 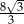 D)
D) 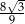
W ostrosłupie prawidłowym czworokątnym krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Wynika stąd, że cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
A) 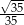 B)
B) 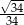 C)
C) 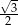 D)
D) 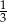
Podstawą ostrosłupa jest kwadrat 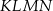 o boku długości 4. Wysokością tego ostrosłupa jest krawędź
o boku długości 4. Wysokością tego ostrosłupa jest krawędź 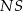 , a jej długość jest równa 6 (zobacz rysunek).
, a jej długość jest równa 6 (zobacz rysunek).
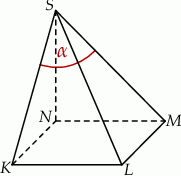
Kąt  , jaki tworzą krawędzie
, jaki tworzą krawędzie 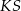 i
i 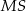 , spełnia warunek
, spełnia warunek
A) 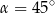 B)
B) 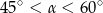 C)
C) 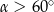 D)
D) 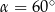
Obwód podstawy ostrosłupa prawidłowego siedmiokątnego jest równy 33,6 cm, a długość jego krawędzi bocznej jest równa 2,5 cm. Pole powierzchni bocznej tego ostrosłupa jest równe
A) 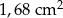 B)
B) 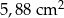 C)
C) 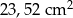 D)
D) 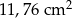
Przekątna podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od wysokości ostrosłupa. Ostrosłup przecięto płaszczyzną przechodzącą przez przekątną podstawy i środek jednej z krawędzi bocznych (patrz rysunek).
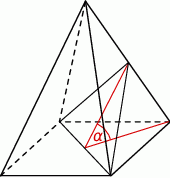
Płaszczyzna przekroju tworzy z podstawą ostrosłupa kąt  o mierze
o mierze
A) 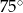 B)
B) 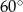 C)
C) 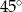 D)
D) 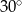
Ostrosłupy prawidłowe trójkątne 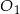 i
i 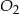 mają takie same wysokości. Długość krawędzi podstawy ostrosłupa
mają takie same wysokości. Długość krawędzi podstawy ostrosłupa 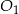 jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa
jest trzy razy dłuższa od długości krawędzi podstawy ostrosłupa 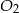 . Stosunek objętości ostrosłupa
. Stosunek objętości ostrosłupa 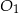 do objętości ostrosłupa
do objętości ostrosłupa 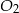 jest równy
jest równy
A) 3 : 1 B) 1 : 3 C) 9 : 1 D) 1 : 9
