Rozwiązaniem równania 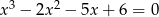 nie jest liczba
nie jest liczba
A) 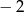 B) 1 C) 4 D) 3
B) 1 C) 4 D) 3
/Szkoła średnia/Zadania testowe/Równania/Wielomianowe
Suma wszystkich pierwiastków równania 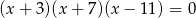 jest równa
jest równa
A) 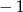 B) 21 C) 1 D)
B) 21 C) 1 D) 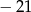
Suma wszystkich rozwiązań równania 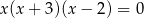 jest równa
jest równa
A) 0 B) 1 C) 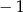 D) 6
D) 6
Suma wszystkich pierwiastków równania 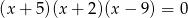 jest równa
jest równa
A) 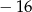 B) 2 C) 16 D)
B) 2 C) 16 D) 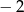
Iloczyn wszystkich pierwiastków równania 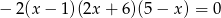 jest równy
jest równy
A) 15 B) 30 C) 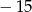 D)
D) 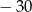
Suma wszystkich rozwiązań równania 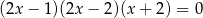 jest równa
jest równa
A) 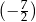 B)
B) 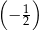 C)
C) 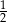 D) 1
D) 1
Suma wszystkich rozwiązań równania 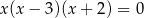 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Iloczyn wszystkich rozwiązań równania 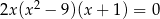 jest równy
jest równy
A) 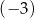 B) 3 C) 0 D) 9
B) 3 C) 0 D) 9
Jednym z rozwiązań równania 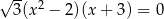 jest liczba
jest liczba
A) 3 B) 2 C) 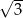 D)
D) 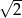
Jednym z rozwiązań równania 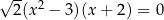 jest liczba
jest liczba
A) 3 B) 2 C) 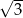 D)
D) 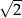
Suma pierwiastków wielomianu 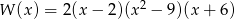 jest równa
jest równa
A) 5 B) 8 C) 4 D) -4
Suma pierwiastków wielomianu 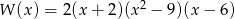 jest równa
jest równa
A) 5 B) 8 C) 4 D) -4
Suma wszystkich pierwiastków równania: 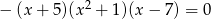 jest równa
jest równa
A) 0 B) 2 C) 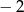 D) 1
D) 1
Suma pierwiastków wielomianu 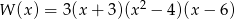 jest równa
jest równa
A) 3 B) 7 C) -7 D) -3
Wskaż równanie, dla którego suma wszystkich rozwiązań jest równa 0.
A) 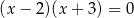 B)
B) 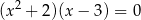
C) 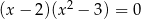 D)
D) 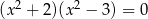
Jednym z rozwiązań równania 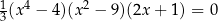 jest liczba
jest liczba
A) 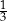 B)
B) 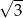 C)
C) 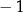 D)
D) 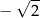
Suma odwrotności pierwiastków wielomianu 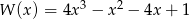 jest równa
jest równa
A) 4 B) 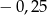 C) 6 D)
C) 6 D) 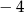
Liczba pierwiastków wielomianu 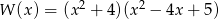 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba różnych miejsc zerowych wielomianu 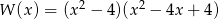 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Iloczyn pierwiastków równania 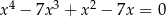 jest równy
jest równy
A) 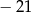 B) 14 C)
B) 14 C) 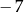 D) 0
D) 0
Równanie 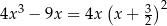 w zbiorze liczb rzeczywistych
w zbiorze liczb rzeczywistych
A) nie ma rozwiązań.
B) ma dokładnie jedno rozwiązanie.
C) ma dokładnie dwa rozwiązania.
D) ma dokładnie trzy rozwiązania.
Wśród miejsc zerowych wielomianu są liczby 0, 1, 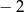 . Wielomian może mieć postać:
. Wielomian może mieć postać:
A) 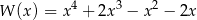 B)
B) 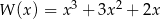
C) 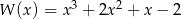 D)
D) 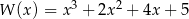
Dany jest wielomian 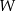 określony wzorem
określony wzorem 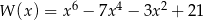 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wielomian
. Wielomian 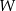 przy rozkładzie na czynniki ma postać
przy rozkładzie na czynniki ma postać
A) 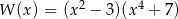 B)
B) 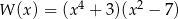
C) 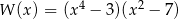 D)
D) 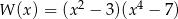
Które z równań jest sprzeczne w zbiorze liczb rzeczywistych?
A) 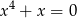 B)
B) 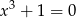 C)
C) 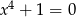 D)
D) 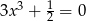
Liczba niewymiernych pierwiastków równania 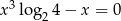 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba niewymiernych pierwiastków równania 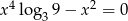 jest równa
jest równa
A) 3 B) 2 C) 1 D) 0
Liczba niewymiernych pierwiastków równania 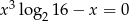 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba niewymiernych pierwiastków równania 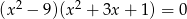 jest równa
jest równa
A) 0 B) 2 C) 3 D) 4
Liczba niewymiernych pierwiastków równania 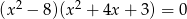 jest równa
jest równa
A) 4 B) 3 C) 2 D) 0
Liczba niewymiernych pierwiastków równania 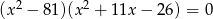 jest równa
jest równa
A) 0 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 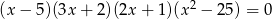 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 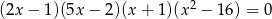 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba ujemnych pierwiastków równania 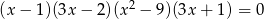 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba pierwiastków wielomianu 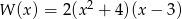 jest równa
jest równa
A) 4 B) 3 C) 2 D) 1
Liczba rozwiązań równania 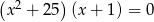 to
to
A) 3 B) 2 C) 1 D) 0
Liczba pierwiastków rzeczywistych wielomianu 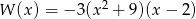 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Suma wszystkich rozwiązań równania 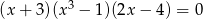 jest równa
jest równa
A) 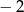 B)
B) 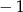 C) 0 D) 2
C) 0 D) 2
Iloczyn wszystkich rozwiązań równania 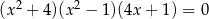 jest równy
jest równy
A) 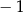 B)
B) 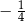 C)
C) 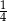 D) 1
D) 1
Dany jest wielomian 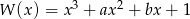 , gdzie
, gdzie  i
i 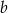 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Równanie 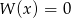 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
B) Jeżeli równanie 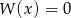 ma pierwiastek całkowity, to
ma pierwiastek całkowity, to 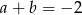 .
.
C) Jeżeli równanie 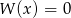 ma ujemny pierwiastek wymierny, to
ma ujemny pierwiastek wymierny, to 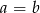 .
.
D) Równanie 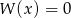 może nie mieć rozwiązań.
może nie mieć rozwiązań.
Dany jest wielomian 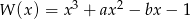 , gdzie
, gdzie  i
i 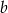 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 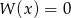 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 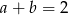 .
.
B) Jeżeli równanie 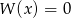 ma dodatni pierwiastek całkowity, to
ma dodatni pierwiastek całkowity, to 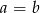 .
.
C) Równanie 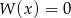 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 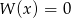 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.
Dany jest wielomian 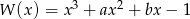 , gdzie
, gdzie  i
i 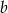 są liczbami całkowitymi. Zatem
są liczbami całkowitymi. Zatem
A) Jeżeli równanie 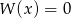 ma pierwiastek wymierny, to
ma pierwiastek wymierny, to 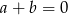 .
.
B) Jeżeli równanie 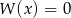 ma ujemny pierwiastek całkowity, to
ma ujemny pierwiastek całkowity, to 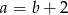 .
.
C) Równanie 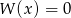 może nie mieć rozwiązań.
może nie mieć rozwiązań.
D) Równanie 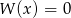 musi mieć co najmniej 2 różne pierwiastki.
musi mieć co najmniej 2 różne pierwiastki.

