Przekrój osiowy walca jest prostokątem, w którym przekątne przecinają się pod kątem 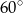 . Wysokość walca jest równa
. Wysokość walca jest równa 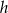 i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
A) 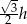 B)
B) 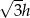 C)
C) 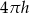 D)
D) 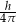
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Walec
Przekrój osiowy walca jest prostokątem, w którym przekątne przecinają się pod kątem 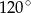 . Wysokość walca jest równa
. Wysokość walca jest równa 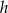 i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
i jest krótsza od średnicy podstawy. Promień podstawy tego walca jest równy
A) 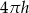 B)
B) 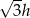 C)
C) 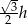 D)
D) 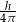
Walec i stożek mają równe promienie podstaw, a wysokość walca jest dwa razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 3 B) 6 C) 2 D) 12
Walec i stożek mają równe promienie podstaw, a wysokość walca jest trzy razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 9 B) 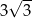 C) 3 D) 27
C) 3 D) 27
Objętość walca o wysokości 8 jest równa 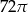 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
Objętość walca o wysokości 4 jest równa 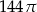 . Promień podstawy tego walca jest równy
. Promień podstawy tego walca jest równy
A) 9 B) 8 C) 6 D) 3
Pole przekroju osiowego walca jest równe 12. Pole powierzchni bocznej tego walca jest równe
A) 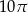 B)
B) 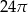 C)
C) 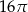 D)
D) 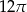
Przekrój osiowy walca jest prostokątem o przekątnej 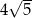 i polu 20. Pole powierzchni bocznej tego walca jest równe
i polu 20. Pole powierzchni bocznej tego walca jest równe
A) 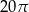 B)
B) 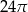 C)
C) 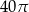 D)
D) 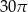
Prostokąt o bokach 4 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 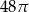 B)
B) 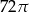 C)
C) 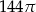 D)
D) 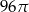
Prostokąt o bokach 10 i 6 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 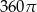 B)
B) 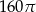 C)
C) 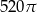 D)
D) 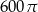
Prostokąt o bokach 3 i 5 obracając się dookoła prostej zawierającej dłuższy bok wyznacza bryłę o objętości równej
A) 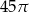 B)
B) 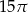 C)
C) 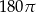 D)
D) 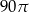
Obwód podstawy walca wynosi 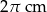 . Wysokość walca jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego walca jest równe
. Wysokość walca jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego walca jest równe
A) 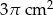 B)
B) 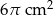 C)
C) 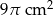 D)
D) 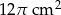
Przekątna przekroju osiowego walca, którego promień podstawy jest równy 4 i wysokość jest równa 6, ma długość
A) 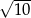 B)
B) 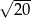 C)
C) 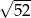 D) 10
D) 10
Przekątna przekroju osiowego walca, którego promień podstawy jest równy 6 i wysokość jest równa 9, ma długość
A) 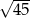 B) 15 C)
B) 15 C) 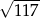 D) 10
D) 10
Pole powierzchni bocznej walca jest równe 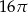 , a promień jego podstawy ma długość 2. Wysokość tego walca jest równa
, a promień jego podstawy ma długość 2. Wysokość tego walca jest równa
A) 4 B) 8 C) 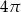 D)
D) 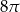
Pole powierzchni bocznej walca jest równe 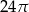 , a promień jego podstawy ma długość 4. Wysokość tego walca jest równa
, a promień jego podstawy ma długość 4. Wysokość tego walca jest równa
A) 6 B) 3 C) 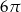 D)
D) 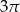
Przekrój osiowy walca jest kwadratem o boku długości 8. Pole powierzchni bocznej tego walca jest równe:
A) 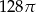 B)
B) 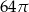 C)
C) 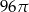 D)
D) 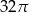
Przekrój osiowy walca jest kwadratem o przekątnej 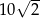 . Pole powierzchni bocznej tego walca jest równe:
. Pole powierzchni bocznej tego walca jest równe:
A) 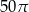 B)
B) 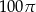 C)
C) 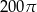 D)
D) 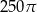
Pole powierzchni bocznej walca jest równe 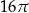 , a promień jego podstawy ma długość 2. Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych. Objętość tego walca jest równa A) 16 B) 32 C)
, a promień jego podstawy ma długość 2. Dokończ zdanie. Zaznacz właściwą odpowiedź spośród podanych. Objętość tego walca jest równa A) 16 B) 32 C) 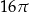 D)
D) 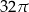
Przekrój osiowy walca jest kwadratem o polu 8. Pole powierzchni całkowitej tego walca jest równe
A) 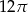 B)
B) 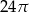 C)
C) 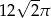 D)
D) 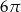
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli  oznacza promień podstawy walca,
oznacza promień podstawy walca, 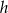 oznacza wysokość walca, to
oznacza wysokość walca, to
A) 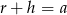 B)
B) 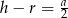 C)
C) 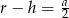 D)
D) 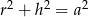
Przekrój osiowy walca jest kwadratem o boku  . Jeżeli
. Jeżeli 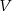 oznacza objętość walca,
oznacza objętość walca, 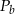 oznacza pole powierzchni bocznej walca, to
oznacza pole powierzchni bocznej walca, to
A) 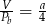 B)
B) 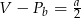 C)
C) 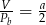 D)
D) 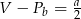
Objętość walca o promieniu podstawy  i wysokości 2 razy większej od promienia jest równa
i wysokości 2 razy większej od promienia jest równa
A) 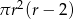 B)
B) 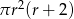 C)
C) 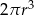 D)
D) 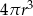
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia dwa razy większa. Objętość tego walca jest równa
A) 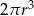 B)
B) 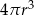 C)
C) 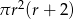 D)
D) 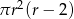
Objętość walca o promieniu podstawy  i wysokości 4 razy mniejszej od promienia jest równa
i wysokości 4 razy mniejszej od promienia jest równa
A) 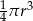 B)
B) 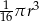 C)
C) 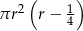 D)
D) 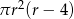
Objętość walca o promieniu podstawy  i wysokości 3 razy większej od promienia jest równa
i wysokości 3 razy większej od promienia jest równa
A) 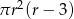 B)
B) 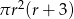 C)
C) 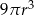 D)
D) 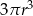
Objętość walca o promieniu podstawy  i wysokości 2 razy mniejszej od promienia jest równa
i wysokości 2 razy mniejszej od promienia jest równa
A) 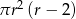 B)
B) 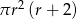 C)
C) 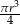 D)
D) 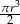
Dany jest walec, w którym promień podstawy jest równy  , a wysokość walca jest od tego promienia o dwa większa. Objętość tego walca jest równa
, a wysokość walca jest od tego promienia o dwa większa. Objętość tego walca jest równa
A) 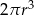 B)
B) 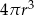 C)
C) 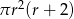 D)
D) 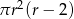
Objętość walca o promieniu podstawy 4 jest równa 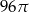 . Pole powierzchni bocznej tego walca jest równe
. Pole powierzchni bocznej tego walca jest równe
A) 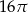 B)
B) 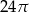 C)
C) 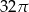 D)
D) 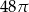
Objętość walca o promieniu podstawy 3 jest równa 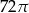 . Pole powierzchni bocznej tego walca jest równe
. Pole powierzchni bocznej tego walca jest równe
A) 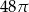 B)
B) 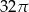 C)
C) 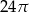 D)
D) 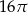
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest kwadratem o polu 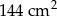 . Jeśli przyjmiemy
. Jeśli przyjmiemy 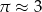 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około
A) 4 cm B) 2 cm C) 12 cm D) 6 cm
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest kwadratem o polu 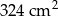 . Jeśli przyjmiemy
. Jeśli przyjmiemy 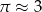 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około
A) 3 cm B) 9 cm C) 6 cm D) 12 cm
Powierzchnia boczna walca po rozwinięciu na płaszczyznę jest kwadratem o polu 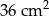 . Jeśli przyjmiemy
. Jeśli przyjmiemy 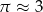 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około
A) 3 cm B) 12 cm C) 6 cm D) 1 cm
Objętość walca, w którym wysokość jest trzykrotnie dłuższa od promienia podstawy, jest równa 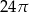 . Zatem promień podstawy tego walca jest ma długość:
. Zatem promień podstawy tego walca jest ma długość:
A) 4 B) 8 C) 2 D) 6
Dany jest walec, w którym wysokość jest równa promieniowi podstawy. Objętość tego walca jest równa 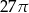 . Wynika stąd, że promień podstawy tego walca jest równy
. Wynika stąd, że promień podstawy tego walca jest równy
A) 9 B) 6 C) 3 D) 2
Objętość walca, w którym wysokość jest trzykrotnie krótsza od promienia podstawy, jest równa 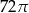 . Zatem promień podstawy tego walca ma długość:
. Zatem promień podstawy tego walca ma długość:
A) 4 B) 8 C) 2 D) 6
Przekrojem osiowym walca jest kwadrat o przekątnej długości 12. Objętość tego walca jest zatem równa
A) 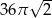 B)
B) 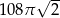 C)
C) 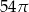 D)
D) 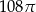
Przekrojem osiowym walca jest kwadrat o przekątnej długości 16. Objętość tego walca jest zatem równa
A) 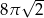 B)
B) 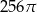 C)
C) 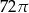 D)
D) 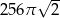
Wysokość walca jest równa promieniowi jego podstaw. Jeśli 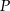 oznacza sumę pól podstaw tego walca, zaś
oznacza sumę pól podstaw tego walca, zaś 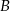 pole jego powierzchni bocznej, to
pole jego powierzchni bocznej, to
A) 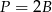 B)
B) 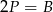 C)
C) 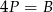 D)
D) 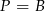
Wysokość walca jest dwa razy większa od promienia jego podstaw. Jeśli 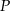 oznacza sumę pól podstaw tego walca, zaś
oznacza sumę pól podstaw tego walca, zaś 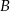 pole jego powierzchni bocznej, to
pole jego powierzchni bocznej, to
A) 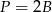 B)
B) 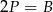 C)
C) 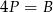 D)
D) 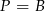
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 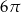 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 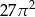 B)
B) 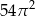 C)
C) 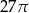 D)
D) 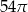
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 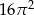 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 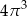 B)
B) 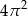 C)
C) 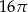 D)
D) 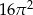
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 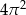 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 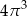 B)
B) 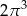 C)
C) 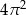 D)
D) 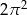
Powierzchnia boczna walca po rozwinięciu jest kwadratem o polu 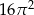 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 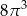 B)
B) 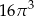 C)
C) 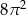 D)
D) 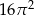
Po rozwinięciu powierzchni bocznej walca na płaszczyźnie otrzymano kwadrat o boku 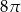 . Objętość tego walca jest równa
. Objętość tego walca jest równa
A) 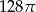 B)
B) 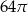 C)
C) 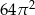 D)
D) 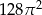
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 4, jest równe
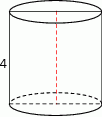
A) 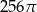 B)
B) 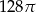 C)
C) 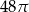 D)
D) 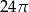
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 6, jest równe
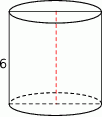
A) 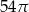 B)
B) 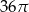 C)
C) 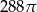 D)
D)