Największą wartością funkcji 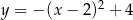 w przedziale
w przedziale 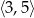 jest
jest
A) 4 B) 3 C) 0 D) 5
/Szkoła średnia
Podstawą ostrosłupa 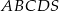 jest prostokąt
jest prostokąt 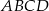 o bokach długości
o bokach długości 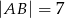 i
i 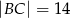 . Krawędź
. Krawędź 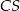 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 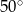 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
Kąt  jest ostry i
jest ostry i 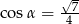 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 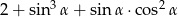 .
.
Rozwiązaniem układu równań 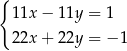 jest para liczb:
jest para liczb: 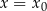 ,
, 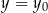 . Wtedy
. Wtedy
A) 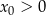 i
i 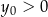 B)
B) 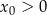 i
i 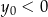 C)
C) 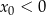 i
i 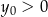 D)
D) 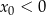 i
i 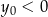
Wartość wyrażenia 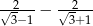 jest równa
jest równa
A) 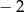 B)
B) 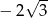 C) 2 D)
C) 2 D) 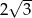
Na rysunku jest przedstawiony fragment wykresu funkcji 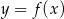 .
.
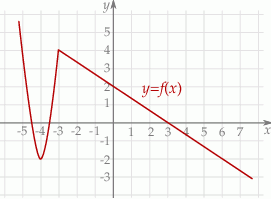
W przedziale 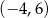 równanie
równanie 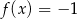
A) nie ma rozwiązań.
B) ma dokładnie dwa rozwiązania.
C) ma dokładnie trzy rozwiązania.
D) ma nieskończenie wiele rozwiązań.
Rozwiąż równanie 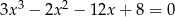 .
.
Wykaż, że dla każdej liczby rzeczywistej  i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 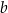 takiej, że
takiej, że 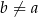 , prawdziwa jest nierówność
, prawdziwa jest nierówność
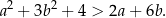
Punkty 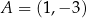 oraz
oraz 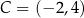 są końcami przekątnej
są końcami przekątnej 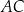 rombu
rombu 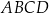 . Środek przekątnej
. Środek przekątnej 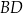 tego rombu ma współrzędne
tego rombu ma współrzędne
A) 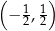 B)
B) 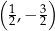 C)
C) 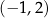 D)
D) 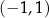
Wielkości  i
i 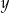 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 |  | 3 | 8 |
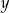 | 36 | 24 | 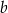 |
Stąd wynika, że
A) 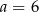 ,
, 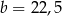 B)
B) 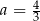 ,
, 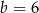 C)
C) 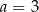 ,
, 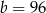 D)
D) 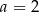 ,
, 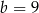
Pięciokąt 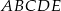 jest foremny. Wskaż trójkąt przystający do trójkąta
jest foremny. Wskaż trójkąt przystający do trójkąta 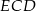
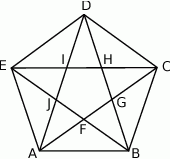
A) 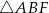 B)
B) 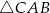 C)
C) 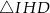 D)
D) 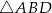
Ile liczb całkowitych  spełnia nierówność
spełnia nierówność 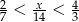 ?
?
A) 14 B) 15 C) 16 D) 17
Jedną z liczb, które spełniają nierówność 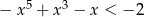 , jest
, jest
A) 1 B) 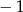 C) 2 D)
C) 2 D) 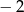
Punkty 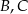 i
i 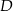 leżą na okręgu o środku
leżą na okręgu o środku 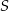 i promieniu
i promieniu  . Punkt
. Punkt 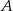 jest punktem wspólnym prostych
jest punktem wspólnym prostych 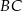 i
i 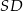 , a odcinki
, a odcinki 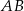 i
i 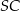 są równej długości. Miara kąta
są równej długości. Miara kąta 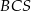 jest równa
jest równa 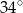 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
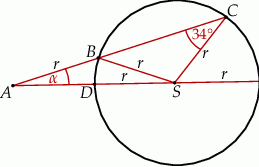
A) 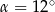 B)
B) 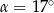 C)
C) 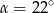 D)
D) 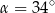
Średnia arytmetyczna cen sześciu akcji na giełdzie jest równa 500 zł. Za pięć z tych akcji zapłacono 2300 zł. Cena szóstej akcji jest równa
A) 400 zł B) 500 zł C) 600 zł D) 700 zł
Uzasadnij, że jeżeli  jest kątem ostrym, to
jest kątem ostrym, to 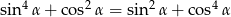 .
.
W ciągu arytmetycznym 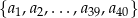 suma wyrazów tego ciągu o numerach parzystych jest równa 1340, a suma wyrazów ciągu o numerach nieparzystych jest równa 1400. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
suma wyrazów tego ciągu o numerach parzystych jest równa 1340, a suma wyrazów ciągu o numerach nieparzystych jest równa 1400. Wyznacz ostatni wyraz tego ciągu arytmetycznego.
W układzie współrzędnych punkty 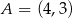 i
i 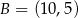 są wierzchołkami trójkąta
są wierzchołkami trójkąta 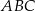 . Wierzchołek
. Wierzchołek 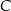 leży na prostej o równaniu
leży na prostej o równaniu 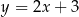 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 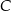 , dla którego kąt
, dla którego kąt 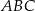 jest prosty.
jest prosty.
Dane są dwie prostokątne działki. Działka pierwsza ma powierzchnię równą 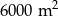 . Działka druga ma wymiary większe od wymiarów pierwszej działki o 10 m i 15 m oraz powierzchnię większą o
. Działka druga ma wymiary większe od wymiarów pierwszej działki o 10 m i 15 m oraz powierzchnię większą o 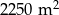 . Oblicz wymiary pierwszej działki.
. Oblicz wymiary pierwszej działki.
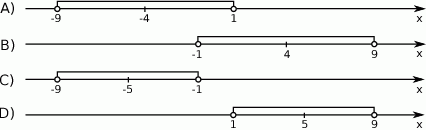
Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 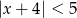 .
.