Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego równa się 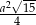 , gdzie
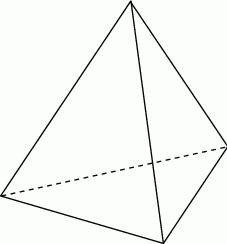
, gdzie  oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem
oznacza długość krawędzi podstawy tego ostrosłupa. Zaznacz na poniższym rysunku kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy. Miarę tego kąta oznacz symbolem 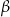 . Oblicz
. Oblicz 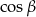 i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość
i korzystając z tablic funkcji trygonometrycznych i odczytaj przybliżoną wartość 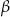 z dokładnością do
z dokładnością do 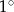 .
.

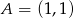 i
i 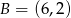 są wierzchołkami trójkąta
są wierzchołkami trójkąta 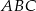 . Wysokości trójkąta
. Wysokości trójkąta 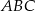 przecinają się w punkcie
przecinają się w punkcie 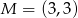 . Oblicz pole tego trójkąta.
. Oblicz pole tego trójkąta. 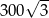
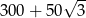
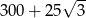
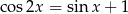 w przedziale
w przedziale 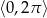 .
. 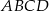 jest trójkąt
jest trójkąt 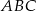 . Krawędź
. Krawędź 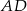 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek). 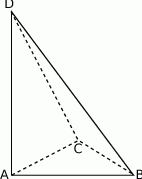
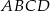 , jeśli wiadomo, że
, jeśli wiadomo, że 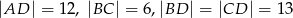 .
. 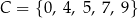 oraz
oraz 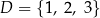 . Losujemy jedną liczbę ze zbioru
. Losujemy jedną liczbę ze zbioru 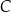 , a następnie losujemy jedną liczbę ze zbioru
, a następnie losujemy jedną liczbę ze zbioru 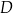 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 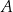 polegającego na tym, że suma wylosowanych liczb będzie większa od 9.
polegającego na tym, że suma wylosowanych liczb będzie większa od 9. 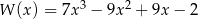 ma dokładnie jeden pierwiastek rzeczywisty. Oblicz ten pierwiastek.
ma dokładnie jeden pierwiastek rzeczywisty. Oblicz ten pierwiastek. 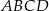 o podstawach
o podstawach 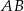 i
i 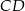 przekątne
przekątne 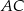 oraz
oraz 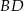 przecinają się w punkcie
przecinają się w punkcie 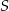 . Wykaż, że jeżeli
. Wykaż, że jeżeli 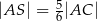 , to pole trójkąta
, to pole trójkąta 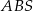 jest 25 razy większe od pola trójkąta
jest 25 razy większe od pola trójkąta  .
. 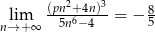 . Wynika stąd, że
. Wynika stąd, że 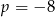
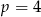
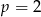
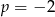
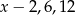 , w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba
, w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba  jest równa
jest równa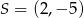 jest środkiem odcinka
jest środkiem odcinka 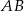 , gdzie
, gdzie 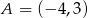 i
i 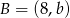 . Wtedy
. Wtedy 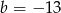
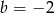
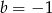
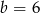
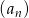 jest określony wzorem
jest określony wzorem 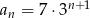 , dla
, dla 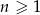 . Oblicz iloraz
. Oblicz iloraz 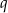 tego ciągu.
tego ciągu. 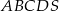 o podstawie
o podstawie 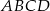 . W trójkącie równoramiennym
. W trójkącie równoramiennym 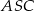 stosunek długości podstawy do długości ramienia jest równy
stosunek długości podstawy do długości ramienia jest równy 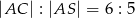 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy. 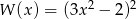 jest równy wielomianowi
jest równy wielomianowi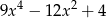
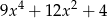
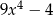
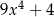
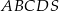 jest kwadrat
jest kwadrat 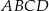 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. 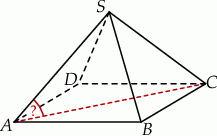
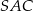 jest równa
jest równa 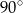
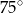
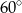
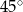
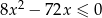 .
. 