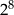Kąt  jest ostry i
jest ostry i 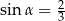 . Wtedy
. Wtedy 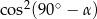 jest równy
jest równy
A)  B)
B)  C)
C)  D)
D) 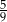
/Szkoła średnia
Rozwiąż równanie 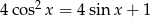 w przedziale
w przedziale 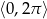 .
.
Dany jest wykres funkcji logarytmicznej 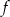 .
.
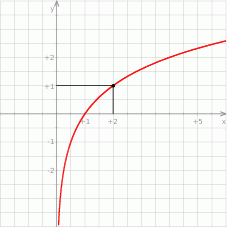
- Wyznacz wzór funkcji
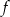 .
. - Narysuj wykres funkcji
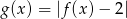 .
. - Odczytaj z rysunku zbiór argumentów, dla których wartości funkcji
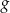 są nie mniejsze od wartości funkcji
są nie mniejsze od wartości funkcji 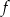 .
.
Wskaż nierówność, którą spełnia liczba 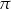 .
.
A) 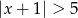 B)
B) 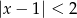 C)
C) 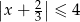 D)
D) 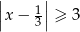
Niech 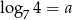 . Wyznacz
. Wyznacz 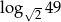 w zależności od
w zależności od  .
.
Dana jest prosta o równaniu 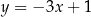 . Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu
. Obrazem tej prostej w symetrii środkowej względem początku układu współrzędnych jest prosta o równaniu
A) 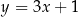 B)
B) 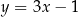 C)
C) 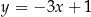 D)
D) 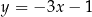
W ciągu arytmetycznym 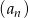 , określonym dla
, określonym dla 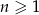 , dane są: wyraz
, dane są: wyraz 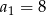 i suma trzech początkowych wyrazów tego ciągu
i suma trzech początkowych wyrazów tego ciągu 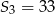 . Oblicz różnicę
. Oblicz różnicę 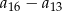 .
.
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 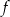 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 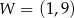 . Liczby
. Liczby 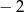 i 4 to miejsca zerowe funkcji
i 4 to miejsca zerowe funkcji 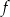 .
.
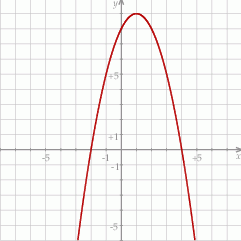
Zbiorem wartości funkcji 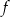 jest przedział
jest przedział
A) 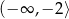 B)
B) 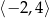 C)
C) 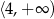 D)
D) 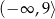
Kąt środkowy oparty na łuku, którego długość jest równa 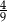 długości okręgu, ma miarę
długości okręgu, ma miarę
A) 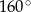 B)
B) 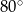 C)
C) 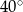 D)
D) 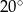
W chwili początkowej (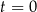 ) zainicjowano pewną reakcję chemiczną, w której brał udział związek
) zainicjowano pewną reakcję chemiczną, w której brał udział związek 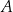 . W wyniku tej reakcji masa
. W wyniku tej reakcji masa 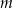 związku
związku 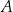 zmieniała się w czasie zgodnie z zależnością
zmieniała się w czasie zgodnie z zależnością
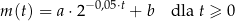
gdzie:
-
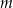 – masa związku
– masa związku 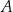 wyrażona w gramach,
wyrażona w gramach, -
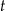 – czas wyrażony w sekundach (liczony od chwili
– czas wyrażony w sekundach (liczony od chwili 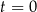 ),
), -
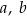 – współczynniki liczbowe.
– współczynniki liczbowe.
Masa początkowa związku 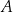 (tj. masa w chwili
(tj. masa w chwili 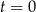 ) była równa
) była równa 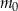 gramów. Po osiągnięciu stanu równowagi (tj. gdy
gramów. Po osiągnięciu stanu równowagi (tj. gdy 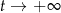 ) masa tego związku była równa
) masa tego związku była równa 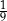 jego masy początkowej (zobacz rysunek).
jego masy początkowej (zobacz rysunek).
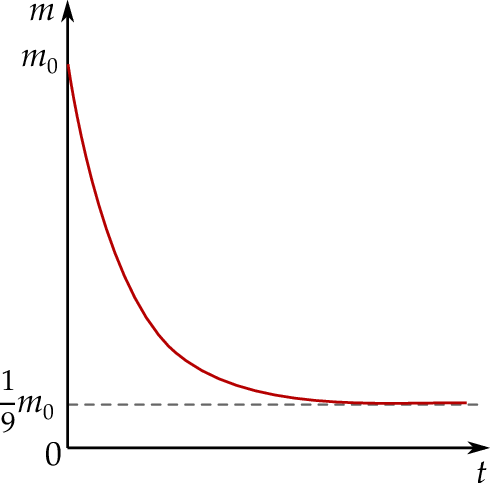
Oblicz, po ilu sekundach (licząc od chwili zainicjowania tej reakcji) przereagowało 87,5% masy początkowej tego związku.
Równość 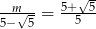 zachodzi dla
zachodzi dla
A) 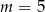 B)
B) 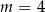 C)
C) 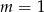 D)
D) 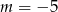
Przekątne rombu 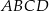 przecinają się w punkcie
przecinają się w punkcie 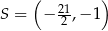 . Punkty
. Punkty 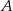 i
i 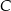 leżą na prostej o równaniu
leżą na prostej o równaniu 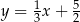 . Wyznacz równanie prostej
. Wyznacz równanie prostej 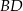 .
.
Z urny zawierającej 10 kul ponumerowanych kolejnymi liczbami od 1 do 10 losujemy jednocześnie trzy kule. Oblicz prawdopodobieństwo zdarzenia 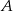 polegającego na tym, że numer jednej z wylosowanych kul jest równy sumie numerów dwóch pozostałych kul.
polegającego na tym, że numer jednej z wylosowanych kul jest równy sumie numerów dwóch pozostałych kul.
Funkcja kwadratowa, której zbiorem wartości jest przedział 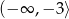 , może być określona wzorem
, może być określona wzorem
A) 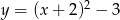 B)
B) 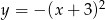 C)
C) 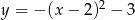 D)
D) 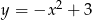
W pudełku znajduje się 8 piłeczek oznaczonych kolejnymi liczbami naturalnymi od 1 do 8. Losujemy jedną piłeczkę, zapisujemy liczbę na niej występującą, a następnie zwracamy piłeczkę do urny. Tę procedurę wykonujemy jeszcze dwa razy i tym samym otrzymujemy zapisane trzy liczby. Oblicz prawdopodobieństwo wylosowania takich piłeczek, że iloczyn trzech zapisanych liczb jest podzielny przez 4. Wynik podaj w postaci ułamka zwykłego.
Iloczyn 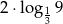 jest równy
jest równy
A) 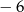 B)
B) 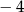 C)
C) 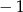 D) 1
D) 1
Wyrażenie 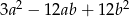 może być przekształcone do postaci
może być przekształcone do postaci
A) 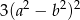 B)
B) 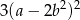 C)
C) 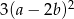 D)
D) 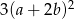
Funkcja 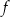 jest określona wzorem
jest określona wzorem 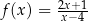 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 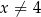 . W kartezjańskim układzie współrzędnych
. W kartezjańskim układzie współrzędnych 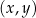 punkt
punkt 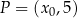 należy do wykresu funkcji
należy do wykresu funkcji 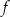 . Oblicz
. Oblicz 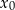 oraz wyznacz równanie stycznej do wykresu funkcji
oraz wyznacz równanie stycznej do wykresu funkcji 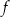 w punkcie
w punkcie 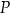 .
.
Średnia arytmetyczna czterech liczb dodatnich: 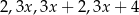 jest równa
jest równa 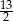 . Wynika stąd, że
. Wynika stąd, że
A) 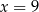 B)
B) 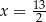 C)
C) 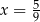 D)
D) 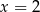
Liczba 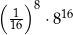 jest równa
jest równa
A) 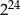 B)
B) 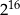 C)
C) 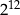 D)
D)