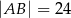W ostrosłupie prawidłowym czworokątnym 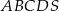 o podstawie
o podstawie 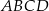 wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 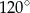 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
/Szkoła średnia
Wyznacz wszystkie wartości parametru  , dla których wykresy funkcji
, dla których wykresy funkcji 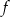 i
i 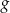 , określonych wzorami
, określonych wzorami 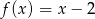 oraz
oraz 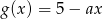 , przecinają się w punkcie o obu współrzędnych dodatnich.
, przecinają się w punkcie o obu współrzędnych dodatnich.
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 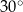 i ma długość równą 6 (zobacz rysunek).
i ma długość równą 6 (zobacz rysunek).
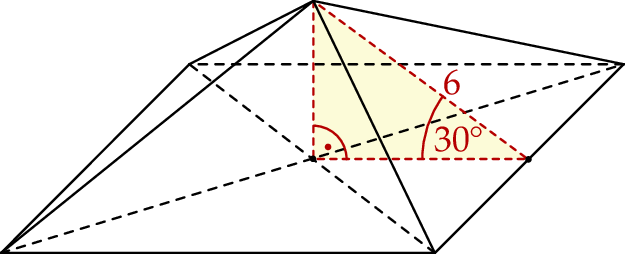
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
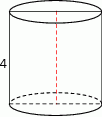
Pole powierzchni całkowitej walca, którego przekrojem osiowym jest kwadrat o boku długości 4, jest równe
A) 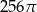 B)
B) 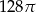 C)
C) 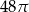 D)
D) 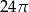
Przy 23-procentowej stawce podatku VAT cena brutto samochodu jest równa 45 018 zł. Jaka jest cena netto tego samochodu?
A) 34 663,86 zł B) 36 600 zł C) 44 995 zł D) 55 372,14 zł
Dany jest ciąg arytmetyczny 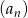 dla
dla 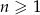 , w którym
, w którym 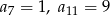 .
.
- Oblicz pierwszy wyraz
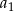 i różnicę
i różnicę  ciągu
ciągu 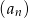 .
. - Sprawdź, czy ciąg
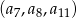 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 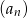 miała wartość najmniejszą.
miała wartość najmniejszą.
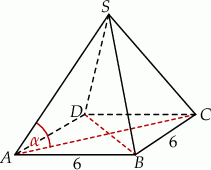
Podstawą ostrosłupa czworokątnego 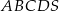 jest trapez
jest trapez 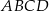 (
(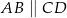 ). Ramiona tego trapezu mają długości
). Ramiona tego trapezu mają długości 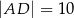 i
i 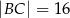 , a miara kąta
, a miara kąta 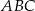 jest równa
jest równa 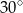 . Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt
. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt  , taki, że
, taki, że 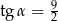 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Średnia arytmetyczna liczb 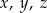 jest równa 4. Średnia arytmetyczna czterech liczb:
jest równa 4. Średnia arytmetyczna czterech liczb:
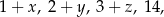
jest równa
A) 6 B) 9 C) 8 D) 13
W rombie o boku długości 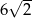 kąt rozwarty ma miarę
kąt rozwarty ma miarę 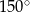 . Iloczyn długości przekątnych tego rombu jest równy
. Iloczyn długości przekątnych tego rombu jest równy
A) 24 B) 72 C) 36 D) 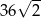
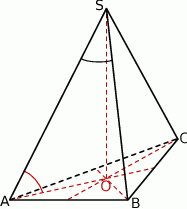
Podstawą ostrosłupa prawidłowego trójkątnego 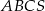 jest trójkąt
jest trójkąt 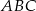 . Kąt nachylenia krawędzi bocznej
. Kąt nachylenia krawędzi bocznej 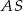 do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi
do płaszczyzny podstawy ostrosłupa jest równy kątowi między krawędziami bocznymi 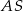 i
i 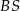 zawartymi w ścianie bocznej
zawartymi w ścianie bocznej 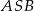 tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
tego ostrosłupa (zob. rysunek). Oblicz kosinus tego kąta.
Kąt  jest ostry i
jest ostry i 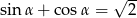 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 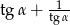 .
.
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego jest równa 6. Pole powierzchni całkowitej tego ostrosłupa jest cztery razy większe od pola jego podstawy. Kąt  jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta
jest kątem nachylenia krawędzi bocznej tego ostrosłupa do płaszczyzny podstawy (zobacz rysunek). Oblicz cosinus kąta  .
.
Rozwiąż równanie 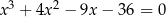 .
.
Na bokach  i
i  równoległoboku
równoległoboku 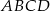 zbudowano kwadraty
zbudowano kwadraty 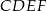 i
i 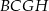 (zobacz rysunek).
(zobacz rysunek).
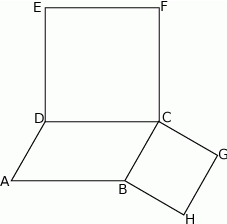
Udowodnij, że 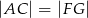 .
.
Wskaż 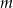 , dla którego funkcja liniowa
, dla którego funkcja liniowa 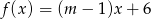 jest rosnąca
jest rosnąca
A) 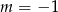 B)
B) 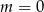 C)
C) 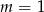 D)
D) 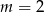
Dany jest trójkąt 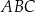 , w którym
, w którym 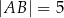 ,
, 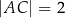 oraz
oraz 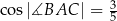 . Długość boku
. Długość boku 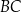 tego trójkąta jest równa
tego trójkąta jest równa
A) 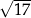 B)
B) 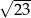 C)
C) 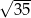 D)
D) 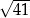
Na rysunku jest przedstawiony wykres funkcji 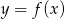 .
.
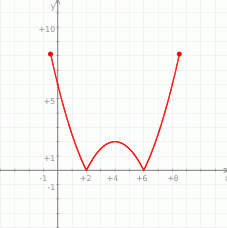
Które równanie ma dokładnie trzy rozwiązania?
A) 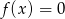 B)
B) 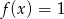 C)
C) 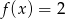 D)
D) 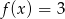
Rozwiąż nierówność 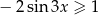 w przedziale
w przedziale 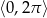 .
.
Punkt 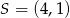 jest środkiem odcinka
jest środkiem odcinka 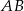 , gdzie
, gdzie 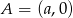 i
i 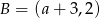 . Wówczas
. Wówczas
A) 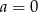 B)
B) 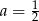 C)
C) 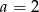 D)
D) 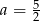
W trapezie 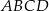 o podstawach
o podstawach 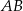 i
i 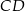 dane są:
dane są: 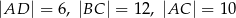 oraz
oraz 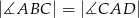 (zobacz rysunek).
(zobacz rysunek).
Wówczas długość podstawy  tego trapezu jest równa
tego trapezu jest równa
A)  B)
B) 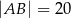 C)
C) 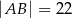 D)
D)