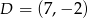Kąt  jest ostry i spełniona jest równość
jest ostry i spełniona jest równość  . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 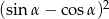 .
.
/Szkoła średnia
Punkty 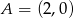 i
i 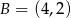 leżą na okręgu o równaniu
leżą na okręgu o równaniu 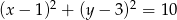 . Wyznacz na tym okręgu taki punkt
. Wyznacz na tym okręgu taki punkt 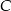 , aby trójkąt
, aby trójkąt 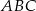 był trójkątem równoramiennym o podstawie
był trójkątem równoramiennym o podstawie 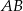 .
.
Punkty 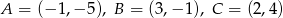 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 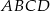 . Oblicz pole tego równoległoboku.
. Oblicz pole tego równoległoboku.
Rozwiąż nierówność 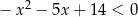 .
.
Ile punktów wspólnych ma prosta 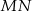 z okręgiem
z okręgiem 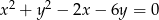 jeśli
jeśli 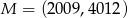 oraz
oraz 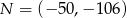 .
.
Kąt rozwarcia stożka ma miarę 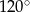 , a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
A) 3 B) 6 C) 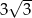 D)
D) 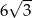
W kartezjańskim układzie współrzędnych 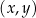 prosta o równaniu
prosta o równaniu 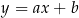 przechodzi przez punkty
przechodzi przez punkty 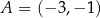 oraz
oraz 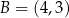 . Współczynnik
. Współczynnik  w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 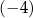 B)
B) 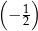 C) 2 D)
C) 2 D) 
Prosta 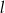 ma równanie
ma równanie 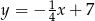 . Wskaż równanie prostej prostopadłej do prostej
. Wskaż równanie prostej prostopadłej do prostej 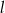 .
.
A) 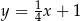 B)
B) 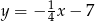 C)
C) 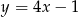 D)
D) 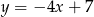
Rozwiąż nierówność 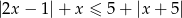 .
.
Oblicz, ile jest liczb naturalnych pięciocyfrowych, w zapisie których nie występuje zero, jest dokładnie jedna cyfra 7 i dokładnie jedna cyfra parzysta.
Boki równoległoboku mają długości 6 i 10, a kąt rozwarty między tymi bokami ma miarę 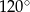 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 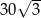 B) 30 C)
B) 30 C) 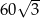 D) 60
D) 60
W kartezjańskim układzie współrzędnych 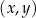 prosta o równaniu
prosta o równaniu 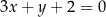 przecina parabolę o równaniu
przecina parabolę o równaniu 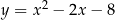 w punktach
w punktach 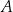 oraz
oraz 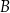 , które są kolejnymi wierzchołkami równoległoboku
, które są kolejnymi wierzchołkami równoległoboku 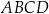 . Wierzchołek
. Wierzchołek 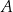 ma pierwszą współrzędną ujemną. Wierzchołek
ma pierwszą współrzędną ujemną. Wierzchołek 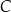 leży na prostej o równaniu
leży na prostej o równaniu 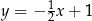 i ma pierwszą współrzędną dodatnią. Odległość punktu
i ma pierwszą współrzędną dodatnią. Odległość punktu 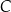 od prostej zawierającej bok
od prostej zawierającej bok 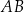 równoległoboku jest równa
równoległoboku jest równa 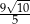 . Oblicz długość boku
. Oblicz długość boku 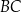 tego równoległoboku.
tego równoległoboku.
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 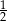 B)
B) 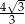 C) 1 D)
C) 1 D) 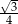
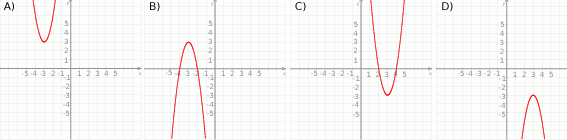
Zbiorem wartości funkcji kwadratowej 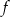 jest przedział
jest przedział 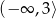 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 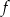 ?
?
W kartezjańskim układzie współrzędnych 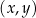 narysowano wykres funkcji
narysowano wykres funkcji 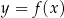 (zobacz rysunek).
(zobacz rysunek).
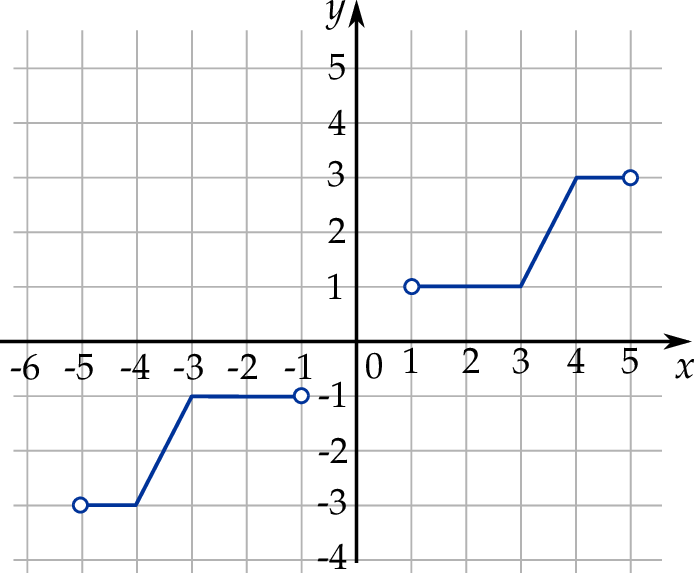
Dziedziną funkcji 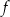 jest zbiór
jest zbiór
A) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zad/9424758/HzadT4x.png) B)
B) 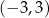 C)
C) 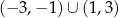
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/9424758/HzadT7x.png) E)
E) 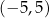 F)
F) 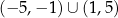
Punkty 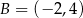 i
i 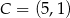 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 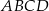 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 74 B) 58 C) 40 D) 29
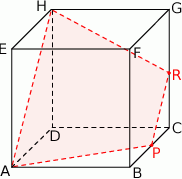
Dany jest sześcian 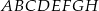 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 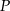 jest środkiem krawędzi
jest środkiem krawędzi 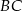 . Płaszczyzna
. Płaszczyzna 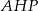 przecina krawędź
przecina krawędź 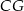 w punkcie
w punkcie 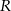 (zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty
(zobacz rysunek). Oblicz pole przekroju tego sześcianu płaszczyzną przechodzącą przez punkty 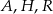 i
i 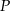 .
.
Wyrażenie 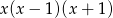 jest równe
jest równe
A) 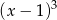 B)
B) 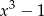 C)
C) 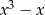 D)
D) 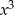
W kartezjańskim układzie współrzędnych 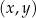 punkty
punkty 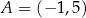 oraz
oraz 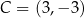 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 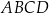 . Pole kwadratu
. Pole kwadratu 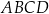 jest równe
jest równe
A) 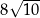 B)
B) 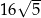 C) 40 D) 80
C) 40 D) 80
Na okręgu o równaniu 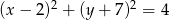 leży punkt
leży punkt
A) 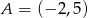 B)
B) 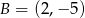 C)
C) 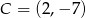 D)
D)