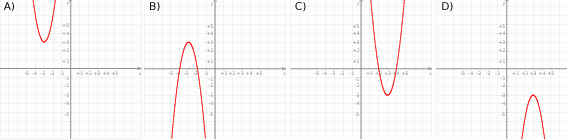
Wskaż wzór funkcji, której wykres ma dokładnie jeden punkt wspólny z prostą 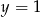 .
.
A) 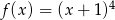 B)
B) 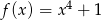 C)
C) 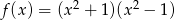 D)
D) 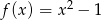
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Różne
Przesuwając wykres funkcji 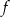 wzdłuż osi
wzdłuż osi 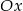 o 6 jednostek w prawo, otrzymano wykres funkcji
o 6 jednostek w prawo, otrzymano wykres funkcji 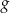 . Zatem
. Zatem
A) 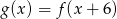 B)
B) 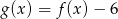 C)
C) 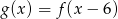 D)
D) 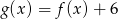
Przesuwając wykres funkcji 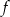 wzdłuż osi
wzdłuż osi 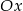 o 6 jednostek w lewo, otrzymano wykres funkcji
o 6 jednostek w lewo, otrzymano wykres funkcji 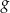 . Zatem
. Zatem
A) 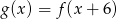 B)
B) 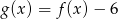 C)
C) 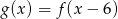 D)
D) 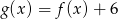
Aby na podstawie wykresu funkcji 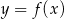 narysować wykres funkcji
narysować wykres funkcji 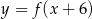 , należy wykres funkcji
, należy wykres funkcji 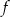 przesunąć o
przesunąć o
A) 6 jednostek do dołu B) 6 jednostek w prawo
C) 6 jednostek do góry D) 6 jednostek w lewo
Aby na podstawie wykresu funkcji 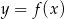 narysować wykres funkcji
narysować wykres funkcji 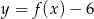 , należy wykres funkcji
, należy wykres funkcji  przesunąć o
przesunąć o
A) 6 jednostek do dołu B) 6 jednostek w prawo
C) 6 jednostek do góry D) 6 jednostek w lewo
Aby na podstawie wykresu funkcji 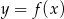 narysować wykres funkcji
narysować wykres funkcji 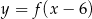 , należy wykres funkcji
, należy wykres funkcji 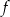 przesunąć o
przesunąć o
A) 6 jednostek do dołu B) 6 jednostek w prawo
C) 6 jednostek do góry D) 6 jednostek w lewo
Prosta o równaniu 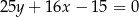 jest prostopadła do stycznej do wykresu funkcji
jest prostopadła do stycznej do wykresu funkcji 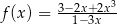 w punkcie
w punkcie
A) 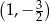 B)
B) 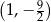 C)
C) 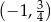 D)
D) 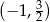
Wykres funkcji 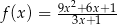 i prosta
i prosta 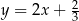
A) pokrywają się B) mają jeden punkt wspólny
C) są rozłączne D) mają dwa punkty wspólne
Wykres funkcji określonej na zbiorze liczb rzeczywistych:
A) musi mieć punkt wspólny z osią 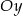 ,
,
B) może mieć dwa punkty wspólne z osią 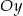 ,
,
C) musi mieć punkt wspólny z osią 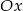 ,
,
D) przechodzi przez początek układu współrzędnych.
Wykres funkcji określonej na zbiorze liczb rzeczywistych:
A) może nie mieć punktów wspólnych z osią 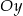 ,
,
B) może mieć dwa punkty wspólne z osią 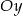 ,
,
C) musi mieć punkt wspólny z osią 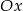 ,
,
D) może mieć dwa punkty wspólnych z osią 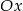 .
.
Wykresem funkcji nie może być:
A) prosta B) punkt C) okrąg D) odcinek
Wykresem funkcji może być:
A) koło B) kwadrat C) okrąg D) odcinek
Funkcja 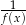 jest określona na całym zbiorze liczb rzeczywistych i nie przyjmuje wartości dodatnich. Na którym rysunku przedstawiono wykres funkcji
jest określona na całym zbiorze liczb rzeczywistych i nie przyjmuje wartości dodatnich. Na którym rysunku przedstawiono wykres funkcji 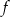 ?
?