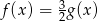Jeżeli 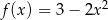 to funkcja
to funkcja 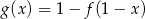 ma wzór
ma wzór
A) 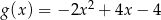 B)
B) 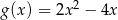
C) 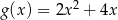 D)
D) 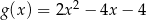
/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa/Różne
Jeżeli funkcja 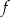 jest określona wzorem
jest określona wzorem 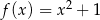 , to funkcję
, to funkcję 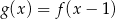 opisuje wzór
opisuje wzór
A) 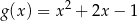 B)
B) 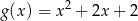
C) 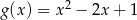 D)
D) 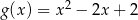
Funkcja kwadratowa 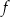 jest określona wzorem
jest określona wzorem 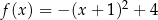 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Wykres funkcji 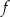 przecina oś przecina oś 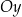 kartezjańskiego układu współrzędnych kartezjańskiego układu współrzędnych 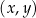 w punkcie o współrzędnych w punkcie o współrzędnych 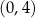 . . | P | F |
Miejsca zerowe funkcji 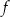 są równe: są równe: 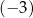 oraz 1. oraz 1. | P | F |
Funkcja kwadratowa 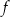 jest określona wzorem
jest określona wzorem 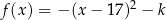 dla pewnej liczby rzeczywistej
dla pewnej liczby rzeczywistej 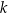 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 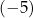 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Drugim miejscem zerowym funkcji 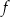 jest liczba 37. jest liczba 37. | P | F |
Największa wartość funkcji 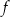 jest równa 484. jest równa 484. | P | F |
Wskaż postać kanoniczną trójmianu 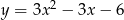 .
.
A) 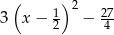 B)
B) 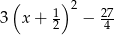 C)
C) 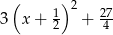 D)
D) 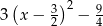
Prosta 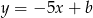 jest styczna do paraboli określonej wzorem
jest styczna do paraboli określonej wzorem 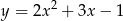 . Liczba
. Liczba 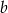 jest równa
jest równa
A) 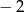 B) 1 C)
B) 1 C) 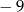 D) 11
D) 11
Funkcja kwadratowa 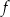 jest określona wzorem
jest określona wzorem 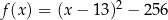 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 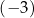 . Drugim miejscem zerowym funkcji
. Drugim miejscem zerowym funkcji 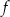 jest liczba
jest liczba
A) 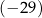 B)
B) 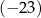 C) 23 D) 29
C) 23 D) 29
Funkcja kwadratowa 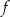 jest określona wzorem
jest określona wzorem 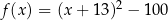 . Jednym z miejsc zerowych tej funkcji jest liczba
. Jednym z miejsc zerowych tej funkcji jest liczba 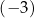 . Drugim miejscem zerowym funkcji
. Drugim miejscem zerowym funkcji 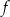 jest liczba
jest liczba
A) 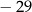 B)
B) 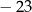 C) 23 D) 29
C) 23 D) 29
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę 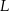 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
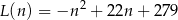
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 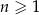 i
i 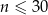 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa 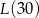 . . | P | F |
| W trzecim dniu analizowanego okresu obsłużono 336 klientów. | P | F |
Właściciel pewnej piekarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 28 kolejnych dni. Przyjmijmy, że liczbę 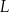 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
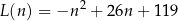
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 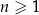 i
i 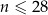 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W piątym dniu analizowanego okresu obsłużono 224 klientów. | P | F |
Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa 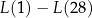 . . | P | F |
Właściciel pewnej pączkarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 40 kolejnych dni. Przyjmijmy, że liczbę 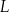 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
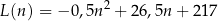
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 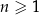 i
i 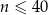 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W jednym z dni poddanych analizie, liczba klientów obsłużonych w pączkarni była równa 448. | P | F |
| W 19 dniu analizowanego okresu obsłużono tyle samo klientów, ile obsłużono w dniu 34. | P | F |
Wskaż postać iloczynową trójmianu 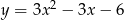 .
.
A) 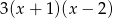 B)
B) 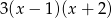 C)
C) 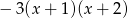 D)
D) 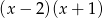
Wskaż postać iloczynową trójmianu 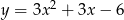 .
.
A) 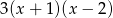 B)
B) 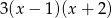 C)
C) 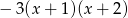 D)
D) 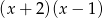
Funkcja kwadratowa 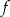 jest określona wzorem
jest określona wzorem 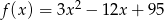 . Zatem wartość
. Zatem wartość 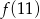 jest równa
jest równa
A) 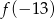 B)
B) 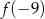 C)
C) 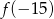 D)
D) 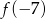
Funkcja 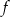 określona jest wzorem
określona jest wzorem 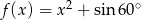 , a funkcja
, a funkcja 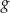 określona jest wzorem
określona jest wzorem 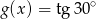 . Wynika stąd, że dla każdej liczby rzeczywistej
. Wynika stąd, że dla każdej liczby rzeczywistej 
A) 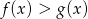 B)
B) 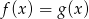 C)
C) 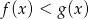 D)
D) 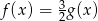
Funkcja 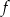 określona jest wzorem
określona jest wzorem 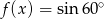 , a funkcja
, a funkcja 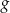 określona jest wzorem
określona jest wzorem 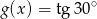 . Wynika stąd, że dla każdej liczby rzeczywistej
. Wynika stąd, że dla każdej liczby rzeczywistej 
A) 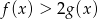 B)
B) 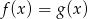 C)
C) 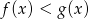 D)
D) 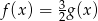
Funkcja 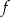 określona jest wzorem
określona jest wzorem 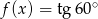 , a funkcja
, a funkcja 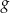 określona jest wzorem
określona jest wzorem 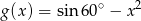 . Wynika stąd, że dla każdej liczby rzeczywistej
. Wynika stąd, że dla każdej liczby rzeczywistej 
A) 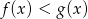 B)
B) 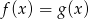 C)
C) 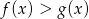 D)
D)