Oblicz pole trójkąta równoramiennego, w którym odległość wierzchołka kąta prostego od przeciwprostokątnej jest równa 5 cm.
/Szkoła podstawowa/Geometria/Trójkąt/Prostokątny
Z wierzchołka kąta prostego trójkąta prostokątnego 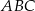 poprowadzono wysokość
poprowadzono wysokość 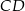 , która podzieliła przeciwprostokątną
, która podzieliła przeciwprostokątną 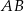 na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
na odcinki o długościach 32 cm i 18 cm (zobacz rysunek).
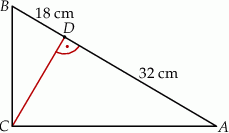
Oblicz pole trójkąta 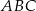 .
.
Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.
Punkt 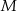 przyprostokątnej
przyprostokątnej 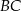 trójkąta prostokątnego
trójkąta prostokątnego 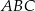 zrzutowano na przeciwprostokątną
zrzutowano na przeciwprostokątną 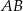 otrzymując punkt
otrzymując punkt 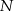 . Wykaż, że
. Wykaż, że 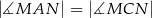 .
.
Oblicz długości odcinka 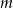 .
.
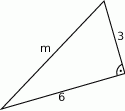
Oblicz długości odcinka 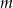 .
.
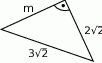
Oblicz długości odcinka 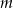 .
.
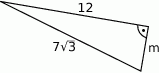
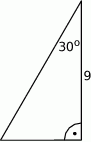
Oblicz pole trójkąta przedstawionego na rysunku.
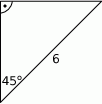
Oblicz pole trójkąta przedstawionego na rysunku.
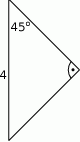
Dany jest trójkąt prostokątny. Wykaż, że suma pól kół o średnicach będących przyprostokątnymi trójkąta jest równa polu koła o średnicy równej przeciwprostokątnej.
Na bokach trójkąta prostokątnego zbudowano trójkąty równoboczne. Wykaż, że pole figury zbudowanej na przeciwprostokątnej jest równe sumie pól figur zbudowanych na przyprostokątnych.
Udowodnij, że jeżeli środek okręgu opisanego na trójkącie leży na jednym z jego boków, to trójkąt ten jest prostokątny.
Oblicz pole trójkąta przedstawionego na rysunku.
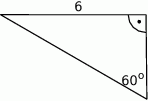
Oblicz pole trójkąta przedstawionego na rysunku.
W trójkącie prostokątnym 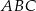 , w którym kąt przy wierzchołku
, w którym kąt przy wierzchołku 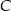 jest kątem prostym, poprowadzono środkowe
jest kątem prostym, poprowadzono środkowe 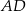 i
i 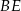 . Udowodnij, że
. Udowodnij, że 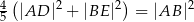 .
.
Liczby 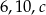 są długościami boków trójkąta prostokątnego. Oblicz
są długościami boków trójkąta prostokątnego. Oblicz  .
.
Punkty 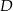 i
i 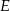 są takimi punktami przeciwprostokątnej
są takimi punktami przeciwprostokątnej 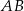 trójkąta prostokątnego
trójkąta prostokątnego 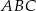 , że
, że 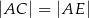 i
i 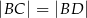 . Wykaż, że
. Wykaż, że 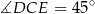 .
.
Oblicz długość odcinka  . Wynik zaokrąglij do pełnych centymetrów.
. Wynik zaokrąglij do pełnych centymetrów.
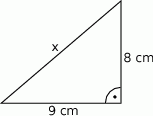
Oblicz długość odcinka  . Wynik zaokrąglij do pełnych centymetrów.
. Wynik zaokrąglij do pełnych centymetrów.
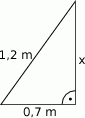
Oblicz długość odcinka  . Wynik zaokrąglij do pełnych centymetrów.
. Wynik zaokrąglij do pełnych centymetrów.
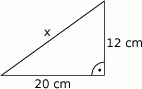
Oblicz długość odcinka  . Wynik zaokrąglij do pełnych centymetrów.
. Wynik zaokrąglij do pełnych centymetrów.
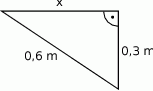
W trójkącie o kątach wewnętrznych 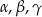 miara kąta
miara kąta  jest równa różnicy miar dwóch pozostałych kątów. Uzasadnij, że ten trójkąt jest prostokątny.
jest równa różnicy miar dwóch pozostałych kątów. Uzasadnij, że ten trójkąt jest prostokątny.
Oblicz wysokość trójkąta prostokątnego o przyprostokątnych 12 cm i 9 cm, która jest poprowadzona do przeciwprostokątnej.
Trójkąt prostokątny ma przyprostokątne długości 6 i 8. Wyznacz długość najkrótszej wysokości tego trójkąta.
Trójkąt prostokątny ma przyprostokątne długości 12 i 5. Wyznacz długość najkrótszej wysokości tego trójkąta.
Wiedząc, że boki trójkąta prostokątnego mają długości: 20, 15, 25, wyznacz długość wysokości opuszczonej na przeciwprostokątną.
Boki trójkąta prostokątnego mają długości 10,24,26. Oblicz długość wysokości opuszczonej na przeciwprostokątną.
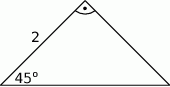
Oblicz pole trójkąta przedstawionego na rysunku.
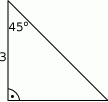
Oblicz pole trójkąta przedstawionego na rysunku.
Dwusieczna kąta ostrego 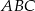 przecina przyprostokątną
przecina przyprostokątną 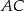 trójkąta prostokątnego
trójkąta prostokątnego 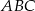 w punkcie
w punkcie 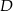 .
.
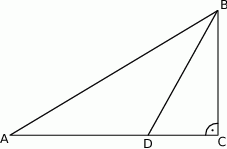
Udowodnij, że jeżeli 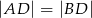 , to
, to 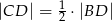 .
.
Dwusieczna kąta ostrego 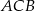 przecina przyprostokątną
przecina przyprostokątną 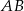 trójkąta prostokątnego
trójkąta prostokątnego 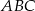 w punkcie
w punkcie 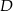 .
.
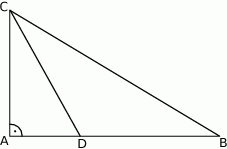
Udowodnij, że jeżeli 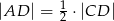 , to
, to 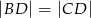 .
.
Sprawdź czy trójkąt jest prostokątny, jeżeli jego boki mają długości: 8 cm, 10 cm, 12 cm.
Sprawdź czy trójkąt jest prostokątny, jeżeli jego boki mają długości: 15 dm, 9 dm, 12 dm.
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 15 cm, a przeciwprostokątna jest o 9 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.
W trójkącie prostokątnym jedna z przyprostokątnych ma długość 10 cm, a przeciwprostokątna jest o 2 cm dłuższa od drugiej przyprostokątnej. Oblicz pole tego trójkąta oraz długość wysokości poprowadzonej z wierzchołka kąta prostego.

