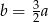Jeśli 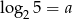 oraz
oraz 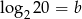 , to liczba
, to liczba 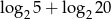 jest równa
jest równa
A) 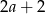 B)
B) 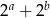 C)
C) 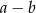 D)
D) 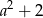
/Szkoła średnia/Zadania testowe/Liczby/Logarytmy/Z literkami/2 literki
Jeżeli 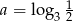 i
i 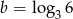 , to liczba
, to liczba  jest równa
jest równa
A) 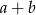 B)
B) 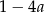 C)
C) 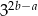 D)
D) 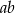
Jeśli 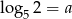 oraz
oraz 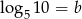 , to liczba
, to liczba 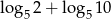 jest równa
jest równa
A) 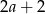 B)
B) 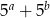 C)
C) 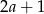 D)
D) 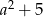
Jeśli 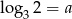 oraz
oraz 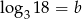 , to liczba
, to liczba 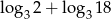 jest równa
jest równa
A) 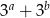 B)
B) 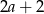 C)
C) 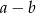 D)
D) 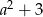
Wiadomo, że 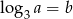 . Wtedy
. Wtedy 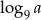 równa się
równa się
A) 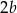 B)
B)  C)
C) 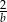 D)
D) 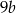
Wiadomo, że 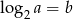 . Wtedy
. Wtedy 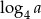 równa się
równa się
A) 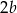 B)
B) 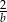 C)
C)  D)
D) 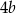
Wiadomo, że 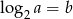 . Wtedy
. Wtedy 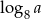 równa się
równa się
A) 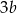 B)
B) 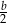 C)
C) 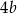 D)
D) 
Wiadomo, że 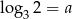 oraz
oraz 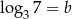 . Zatem
. Zatem 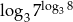 jest równy
jest równy
A) 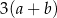 B)
B) 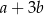 C)
C) 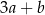 D)
D) 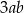
Dla dowolnej liczby rzeczywistej 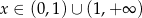 zachodzi zależność
zachodzi zależność 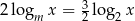 . Wartość parametru
. Wartość parametru 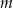 jest równa
jest równa
A)  B)
B) 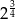 C)
C) 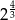 D)
D) 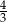
Wiadomo, że 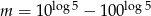 i
i 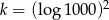 . Zatem
. Zatem
A) 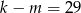 B)
B) 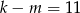 C)
C) 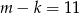 D)
D) 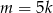
Wiadomo, że 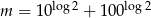 i
i 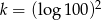 . Zatem
. Zatem
A) 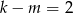 B)
B) 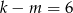 C)
C) 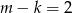 D)
D) 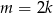
Wiadomo, że 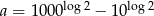 i
i 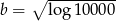 . Zatem
. Zatem
A) 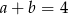 B)
B) 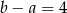 C)
C) 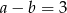 D)
D) 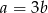
Dane są liczby 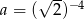 oraz
oraz 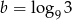 . Zatem
. Zatem
A) 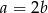 B)
B) 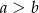 C)
C) 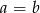 D)
D) 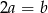
Jeżeli 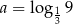 oraz
oraz 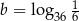 , to
, to
A) 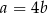 B)
B) 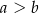 C)
C) 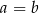 D)
D) 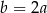
Wiadomo, że 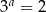 i
i 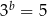 . Zatem liczba
. Zatem liczba 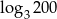 jest równa
jest równa
A) 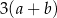 B)
B) 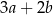 C)
C) 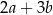 D)
D) 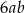
Jeśli 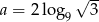 i
i 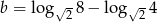 to:
to:
A) 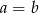 B)
B) 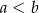 C)
C) 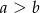 D)
D) 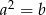
Jeśli 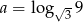 i
i 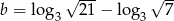 to:
to:
A) 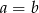 B)
B) 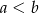 C)
C) 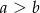 D)
D) 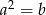
Jeśli 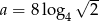 i
i 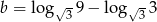 to:
to:
A) 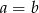 B)
B) 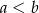 C)
C) 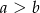 D)
D) 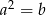
Dla dowolnych liczb 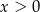 ,
, 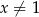 ,
, 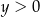 ,
, 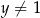 wartość wyrażenia
wartość wyrażenia 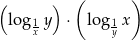 jest równa
jest równa
A) 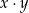 B)
B) 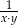 C)
C) 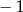 D) 1
D) 1
Dane są liczby 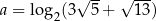 oraz
oraz 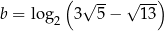 . Liczba
. Liczba 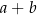 jest równa
jest równa
A) 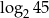 B)
B) 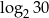 C) 4 D) 5
C) 4 D) 5
Jeżeli 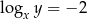 to
to 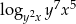 jest równy
jest równy
A) 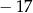 B)
B) 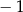 C) 3 D)
C) 3 D) 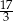
Wiadomo, że 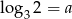 oraz
oraz 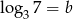 . Zatem
. Zatem 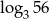 jest równy
jest równy
A) 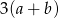 B)
B) 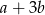 C)
C) 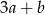 D)
D) 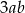
Wiadomo, że 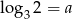 oraz
oraz 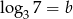 . Zatem
. Zatem 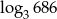 jest równy
jest równy
A) 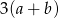 B)
B) 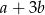 C)
C) 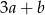 D)
D) 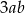
Wiadomo, że 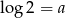 oraz
oraz 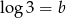 . Zatem
. Zatem 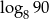 jest równy
jest równy
A) 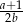 B)
B) 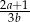 C)
C) 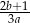 D)
D) 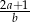
Jeśli 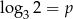 i
i 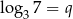 , to
, to 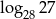 jest równy
jest równy
A) 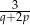 B)
B) 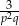 C)
C) 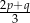 D)
D) 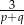
Wiadomo, że 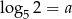 oraz
oraz 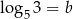 . Wtedy liczba
. Wtedy liczba 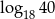 jest równa
jest równa
A) 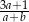 B)
B) 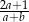 C)
C) 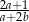 D)
D) 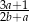
Dane są liczby 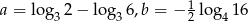 . Zatem
. Zatem
A) 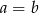 B)
B) 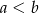 C)
C) 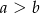 D)
D) 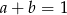
Dane są liczby 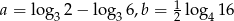 . Zatem
. Zatem
A) 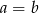 B)
B) 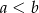 C)
C) 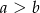 D)
D) 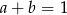
Dane są liczby 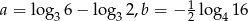 . Zatem
. Zatem
A) 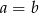 B)
B) 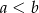 C)
C) 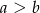 D)
D) 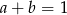
Dla dowolnych liczb 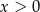 ,
, 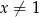 ,
, 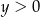 ,
, 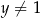 wartość wyrażenia
wartość wyrażenia 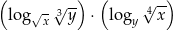 jest równa
jest równa
A) 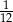 B)
B) 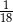 C)
C) 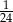 D)
D) 
Wiadomo, że 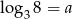 i
i 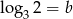 . Wynika stąd, że
. Wynika stąd, że
A) 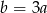 B)
B) 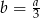 C)
C) 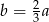 D)
D)