Na diagramie przedstawiono liczbę butelek z wodą dostarczonych do sklepu osiedlowego oraz liczbę butelek z wodą sprzedanych w tym sklepie przez trzy kolejne dni: poniedziałek, wtorek i środę.
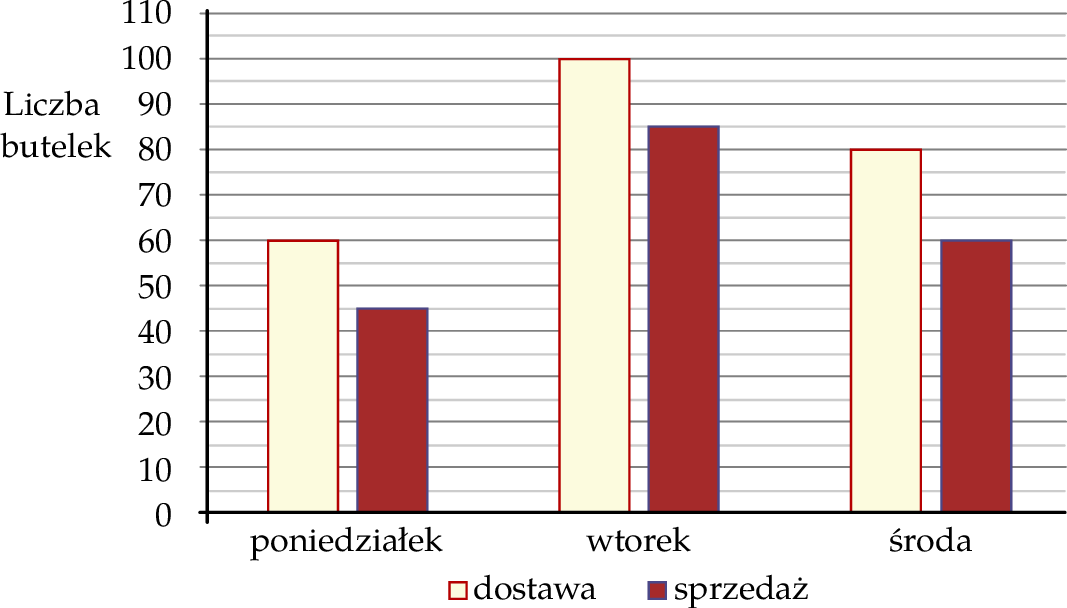
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przez te trzy dni w sklepie osiedlowym sprzedano łącznie 190 butelek z wodą. | P | F |
Liczba butelek z wodą sprzedanych w poniedziałek stanowi  liczby butelek z wodą dostarczonych w tym dniu. liczby butelek z wodą dostarczonych w tym dniu. | P | F |

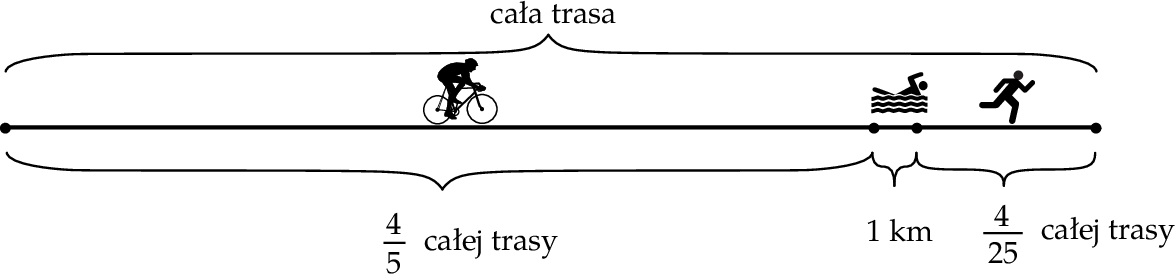


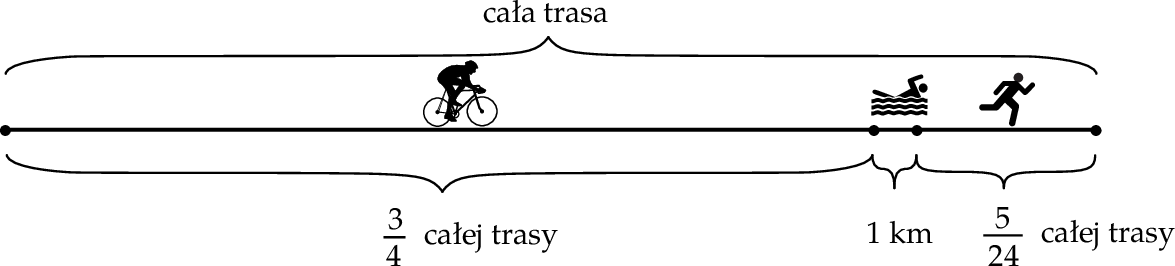
 jest A/B.
jest A/B.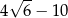 jest C/D.
jest C/D.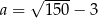 jest A/B.
jest A/B.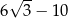 jest C/D.
jest C/D.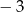 jest większa niż 2?
jest większa niż 2? 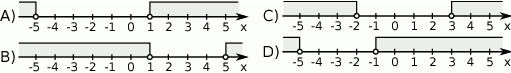
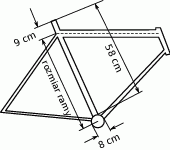
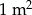
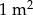 wykładziny welurowej jest niższa niż cena
wykładziny welurowej jest niższa niż cena 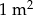 wykładziny wełnianej.
wykładziny wełnianej. 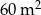 papy. Papa jest sprzedawana w rolkach o szerokości 1 m. Pan Kazimierz pod uwagę wziął dwa rodzaje papy.
papy. Papa jest sprzedawana w rolkach o szerokości 1 m. Pan Kazimierz pod uwagę wziął dwa rodzaje papy. 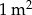
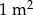 papy I rodzaju jest niższa niż cena
papy I rodzaju jest niższa niż cena 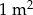 papy II rodzaju.
papy II rodzaju. 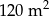 . Pod uwagę wziął dwa rodzaje farb.
. Pod uwagę wziął dwa rodzaje farb. 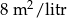
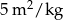
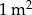 ściany jest niższy w przypadku farby akrylowej, niż w przypadku farby lateksowej.
ściany jest niższy w przypadku farby akrylowej, niż w przypadku farby lateksowej. 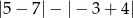 jest równa
jest równa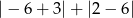 jest równa
jest równa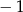
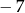
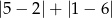 jest równa
jest równa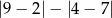 jest równa
jest równa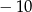
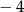
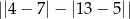 jest równa
jest równa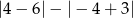 jest równa
jest równa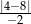 jest równa
jest równa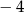
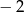
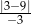 jest równa
jest równa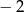
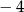
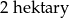 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi: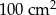
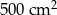
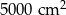
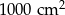
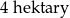 . Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi:
. Pole powierzchni tej działki na planie wykonanym w skali 1:200 wynosi: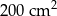
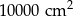
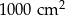
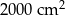
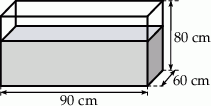
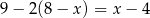 jest liczbą
jest liczbą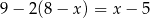 jest liczbą
jest liczbą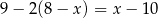 jest liczbą
jest liczbą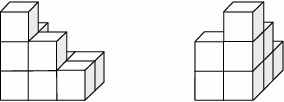
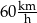 .
.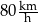 .
. 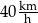 , to czas przejazdu byłby równy 6 godzin.
, to czas przejazdu byłby równy 6 godzin. 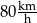 .
.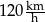 .
. 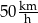 , to czas przejazdu byłby równy 5 godzin.
, to czas przejazdu byłby równy 5 godzin. 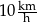 , to pociąg pokonałby tę trasę w czasie o 30 minut krótszym.
, to pociąg pokonałby tę trasę w czasie o 30 minut krótszym.  cukierków. Sam zjadł z tej torebki 8 cukierków, a pozostałe cukierki rozdzielił pomiędzy swoich 5 kolegów. Czworo z tych chłopców otrzymało tyle samo cukierków, a piąty z nich, Szymon, otrzymał o jeden cukierek więcej od pozostałych. Liczba cukierków, które otrzymał Szymon jest równa
cukierków. Sam zjadł z tej torebki 8 cukierków, a pozostałe cukierki rozdzielił pomiędzy swoich 5 kolegów. Czworo z tych chłopców otrzymało tyle samo cukierków, a piąty z nich, Szymon, otrzymał o jeden cukierek więcej od pozostałych. Liczba cukierków, które otrzymał Szymon jest równa 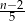
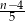
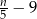
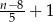
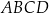 oraz
oraz 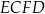 (zobacz rysunek).
(zobacz rysunek). 
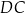 równoległoboku
równoległoboku  jest jedną z wysokości równoległoboku
jest jedną z wysokości równoległoboku 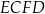 .
. 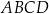 jest równe polu równoległoboku
jest równe polu równoległoboku 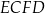 .
. 