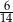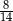W każdym z dwóch pudełek są tylko kule białe i czarne. Prawdopodobieństwo wylosowania kuli czarnej z pierwszego pudełka jest równe 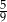 . W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pierwszym pudełku są 4 kule białe. | P | F |
Prawdopodobieństwo wylosowania kuli białej z drugiego pudełka jest równe 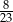 . . | P | F |

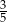 .
. 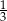
 .
. 
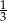 .
.  .
.  . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe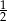
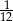
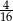

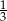
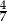 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe

 .
.  .
.