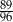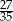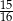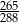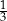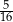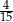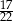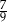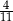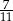W pierwszym pudełku jest 6 kul zielonych i 9 czerwonych, a w drugim są 4 kule zielone i 6 czarnych. Losujemy po jednej kuli z każdego z pudełek. Czy prawdziwe jest stwierdzenie, że prawdopodobieństwo wylosowania zielonej kuli z pierwszego pudełka jest większe, niż prawdopodobieństwo wylosowania zielonej kuli z drugiego pudełka? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w pierwszym pudełku jest więcej kul zielonych niż w drugim pudełku. |
| B) | w każdym z pudełek kule zielone stanowią taki sam procent pozostałych kul. |
| C) | w pierwszym pudełku jest tyle samo kul zielonych, ile jest kul czarnych w drugim pudełku. |




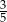


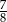

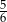
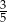
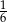

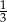
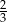
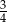

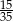
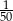
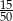
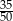


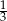

 stanowiły piłeczki czerwone. Wyciągnięto 16 piłeczek, wśród których żadna nie była czerwona. Kasia – jako siedemnasta – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kasię piłeczki czerwonej wynosi
stanowiły piłeczki czerwone. Wyciągnięto 16 piłeczek, wśród których żadna nie była czerwona. Kasia – jako siedemnasta – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kasię piłeczki czerwonej wynosi 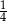
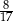
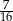
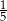
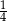 stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Bartek – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Bartka piłeczki czarnej wynosi
stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Bartek – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Bartka piłeczki czarnej wynosi 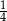
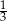
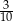
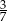
 . Ile kulek zielonych usunięto z pudełka?
. Ile kulek zielonych usunięto z pudełka?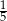 . Na loterię przygotowano A/B losów przegrywających.
. Na loterię przygotowano A/B losów przegrywających.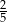

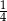 . Ile kulek zielonych dołożono do pudełka?
. Ile kulek zielonych dołożono do pudełka? 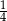 . Ile kulek zielonych dołożono do pudełka?
. Ile kulek zielonych dołożono do pudełka? 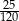
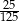
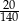
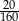
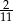
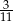
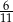
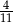
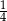 stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Kamil – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kamila piłeczki czarnej wynosi
stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Kamil – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kamila piłeczki czarnej wynosi 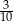 . Liczba wszystkich piłeczek czarnych, które początkowo znajdowały się w pudełku jest równa
. Liczba wszystkich piłeczek czarnych, które początkowo znajdowały się w pudełku jest równa 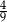
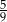
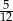
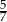
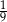
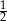
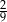

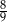
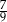
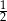

 , a prawdopodobieństwo wylosowania kuli żółtej jest równe
, a prawdopodobieństwo wylosowania kuli żółtej jest równe 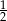 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe. 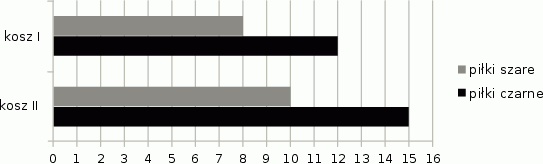
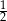 ? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C. 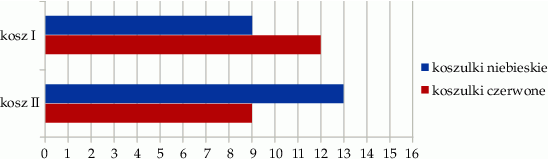
 .
. 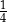 , to znaczy, że połowę wszystkich kul w urnie stanowią kule niebieskie.
, to znaczy, że połowę wszystkich kul w urnie stanowią kule niebieskie. 

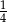
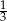
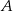 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 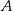 jest równe
jest równe 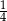
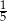
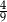
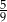


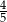

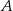 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 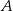 jest równe
jest równe 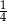
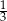
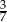

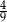

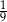
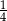
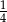
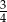
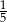


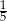
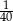
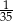
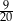
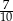
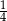
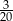
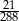 stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe