W pojemniku są wyłącznie kule białe, czerwone, niebieskie i żółte. Kul białych jest tyle samo co kul niebieskich, kul czerwonych jest dwa razy więcej niż kul żółtych, a stosunek liczby kul żółtych do liczby kul niebieskich jest równy 4 : 5. Z pojemnika losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli, która nie jest czerwona jest równe
A) 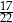 B)
B) 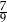 C)
C) 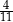 D)
D) 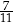
/Szkoła podstawowa/Zadania testowe/Prawdopodobieństwo/Różne
W każdym z dwóch pudełek są tylko kule białe i czarne. Prawdopodobieństwo wylosowania kuli czarnej z pierwszego pudełka jest równe 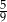 . W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. W drugim pudełku jest dwa razy więcej kul białych i trzy razy więcej kul czarnych niż w pierwszym pudełku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pierwszym pudełku są 4 kule białe. | P | F |
Prawdopodobieństwo wylosowania kuli białej z drugiego pudełka jest równe 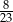 . . | P | F |
Z urny, w której jest wyłącznie 18 kul białych i 12 kul czarnych, losujemy 1 kulę.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wylosowania kuli białej jest równe 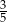 . . | P | F |
Prawdopodobieństwo wylosowania kuli czarnej jest mniejsze od 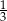 | P | F |
Z urny, w której jest wyłącznie 16 kul białych i 24 kule czarne, losujemy 1 kulę.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wylosowania kuli białej jest równe  . . | P | F |
Prawdopodobieństwo wylosowania kuli czarnej jest większe od  | P | F |
Organizatorzy loterii fantowej przygotowali zestaw losów, w którym były dwa rodzaje losów: niebieskie i zielone. Losów niebieskich było dwa razy mniej niż losów zielonych i upoważniały one do odbioru cenniejszej nagrody. Uczestnicy loterii losowali po jednym losie, który po wylosowaniu był usuwany z zestawu. Pierwszy uczestnik loterii wyciągnął los niebieski, a drugi uczestnik wyciągnął los zielony.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wyciągnięcia przez trzecią osobę losu niebieskiego jest równe 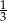 . . | P | F |
Prawdopodobieństwo wyciągnięcia przez pierwszą osobę losu zielonego było równe  . . | P | F |
W szufladzie jest 7 par skarpetek białych i 3 pary skarpetek czarnych. Tomek losuje z szuflady po jednej skarpetce i kładzie ją na stół.
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania czarnej skarpetki jest równe 0,3. | P | F |
| Tomek za pierwszym razem nie wylosował czarnej skarpetki. Prawdopodobieństwo, że za drugim razem wylosuje czarną skarpetkę jest większe. | P | F |
W pudełku było 15 kul białych i 5 czarnych. Dołożono jeszcze 10 kul białych i 20 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
| Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej. | P | F |
W pudełku jest 30 kul białych i 20 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli 10 kul białych zostanie zastąpionych kulami czarnymi, to prawdopodobieństwa wylosowania kuli czarnej i białej będą równe. | P | F |
| Jeżeli podwoimy liczbę kul czarnych w pudełku, to prawdopodobieństwo wylosowania kuli czarnej wzrośnie dwukrotnie. | P | F |
W pudełku znajduje się 6 losów, wśród których są 2 losy wygrywające.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia losu wygrywającego jest dwukrotnie mniejsze, niż wyciągnięcia losu przegrywającego. | P | F |
| Jeśli do pudełka włożymy dodatkowy los wygrywający, to prawdopodobieństwo wygranej wzrośnie. | P | F |
W pudełku było 20 kul białych i 10 czarnych. Dołożono jeszcze 10 kul białych i 15 czarnych. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przed dołożeniem kul prawdopodobieństwo wylosowania kuli białej było trzy razy większe niż prawdopodobieństwo wylosowania kuli czarnej. | P | F |
| Po dołożeniu kul prawdopodobieństwo wylosowania kuli czarnej jest większe niż prawdopodobieństwo wylosowania kuli białej. | P | F |
W szufladzie znajduje się 10 par skarpetek, w tym 3 pary skarpetek czarnych. Tomek losowo wyjmuje po jednej skarpetce z szuflady.
Wybierz P, jeśli zdanie jest prawdziwe, lub F jeśli jest fałszywe.
| Tomek, aby mieć pewność, że przynajmniej dwie wyjęte skarpetki będą czarne, musi wyjąć co najmniej 16 skarpetek. | P | F |
| Tomek za pierwszym razem nie wyjął czarnej skarpetki. Prawdopodobieństwo, że za drugim razem wyjmie czarną skarpetkę, wzrosło. | P | F |
Do pudełka włożono piłki zielone i czerwone. Wszystkich piłek jest 8, a piłek czerwonych jest 6.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia czerwonej piłki jest trzy razy większe, niż prawdopodobieństwo wyciągnięcia piłki zielonej. | P | F |
| Jeśli z pudełka zabierzemy 2 czerwone piłki, to prawdopodobieństwa wyciągnięcia piłki czerwonej i zielonej będą równe. | P | F |
W pudełku znajduje się 18 losów, wśród których są 2 losy wygrywające.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia losu przegrywającego jest dziewięciokrotnie większe, niż wyciągnięcia losu wygrywającego. | P | F |
| Jeżeli do pudełka włożymy dwa losy wygrywające to prawdopodobieństwo wygranej wzrośnie o 100%. | P | F |
W kapeluszu znajdują się króliki białe i szare. Królików szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe  . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
A) 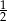 B)
B) 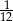 C)
C) 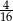 D)
D) 
W woreczku znajdują się piłki białe i szare. Piłek szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z woreczka piłki białej jest równe 0,25. Zatem prawdopodobieństwo wyciągnięcia z woreczka piłki szarej jest równe
A) 0,75 B) 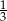 C) 0,25 D) 0,8
C) 0,25 D) 0,8
W kapeluszu znajdują się króliki białe i szare. Prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe 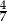 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
A)  B) 0,75 C)
B) 0,75 C)  D)
D) 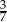
W pudełku znajduje się 30 losów loterii. 5 z tych losów jest wygrywających, 10 jest przegrywających, a wyciągnięcie jednego z pozostałych upoważnia do wyciągnięcia jeszcze jednego losu. Po wyciągnięciu los nie jest zwracany do pudełka. Pierwsza osoba, która brała udział w tej loterii, wyciągnęła los przegrywający.
Czy podane zdania są prawdziwe (P), czy fałszywe (F)?
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu wygrywającego wzrosło. | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu przegrywającego zmalało. | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę losu upoważniającego do ponownego losowania nie zmieniło się. | P | F |
Na rysunku przedstawiono liczbę i rodzaj kul umieszczonych w każdym z czterech pudełek. Z każdego pudełka losujemy jedną kulę.
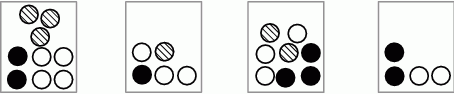
Prawdopodobieństwo wylosowania białej kuli jest największe, gdy kulę losujemy z pudełka
A) 1 B) 2 C) 3 D) 4
W tabeli przedstawiono liczbę i rodzaj kul umieszczonych w czterech pudełkach. Z każdego pudełka losujemy jedną kulę.
| Liczba kul zielonych | Liczba kul niebieskich | Liczba kul czerwonych | |
| Pudełko nr 1 | 4 | 8 | 5 |
| Pudełko nr 2 | 7 | 16 | 9 |
| Pudełko nr 3 | 2 | 7 | 3 |
| Pudełko nr 4 | 7 | 12 | 5 |
Prawdopodobieństwo wylosowania niebieskiej kuli jest największe, gdy kulę losujemy z pudełka nr
A) 1 B) 2 C) 3 D) 4
Organizatorzy konkursu matematycznego przygotowali zestaw, w którym było 10 pytań z algebry i 8 pytań z geometrii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z algebry.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z algebry jest równe 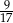 . . | P | F |
| Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z geometrii się nie zmieniło. | P | F |
Organizatorzy konkursu z języka polskiego przygotowali zestaw, w którym było 15 pytań z gramatyki i 7 pytań z ortografii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z gramatyki.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z ortografii zwiększyło się. | P | F |
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z gramatyki jest równe 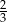 . . | P | F |
W pudełku znajduje się 14 par skarpetek, w tym 8 par skarpetek czerwonych i 6 par skarpetek niebieskich. Ania losowo wybiera z pojemnika 14 skarpetek. Prawdopodobieństwo, że Ania wybrała co najmniej dwie skarpetki czerwone jest równe
A) 1 B) 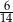 C)
C) 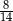 D)
D) 

