W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 3 | 6 | 8 | 4 | 4 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,2 B)  C)
C) 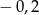 D)
D) 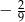
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 3 | 6 | 8 | 4 | 4 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,2 B)  C)
C) 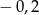 D)
D) 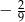
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 5 | 3 | 5 | 7 | 3 | 1 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 3,125 B) 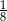 C) 1,125 D)
C) 1,125 D) 
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 2 | 4 | 7 | 2 | 3 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,3 B) 3,3 C) 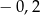 D) 3
D) 3
Wojtek notował temperaturę powietrza o godzinie 12.00 w pięciu kolejnych dniach stycznia. Otrzymał następujące wyniki:
| Data | 15.01 | 16.01 | 17.01 | 18.01 | 19.01 |
| Temperatura | 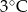 | 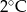 | 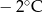 | 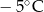 | 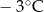 |
Odchylenie standardowe od średniej temperatury w tych dniach, z dokładnością do 0,1 wynosi
A) 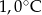 B)
B) 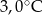 C)
C) 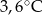 D)
D) 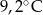
Na diagramie przedstawiono oceny z pracy klasowej z matematyki w klasie IIa.
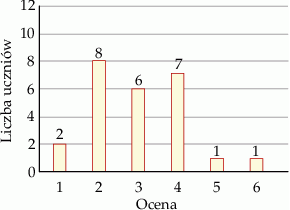
Odchylenie standardowe danych przedstawionych na diagramie jest równe
A) 1,2 B) 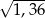 C)
C) 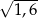 D) 1,6
D) 1,6
Dla zestawu liczb: 1, 3, 2, 4, 3
A) mediana jest równa 2 i średnia arytmetyczna jest równa 2,6.
B) mediana jest równa 3 i średnia arytmetyczna jest równa 3.
C) mediana jest równa 2 i średnia arytmetyczna jest równa 3.
D) mediana jest równa 3 i średnia arytmetyczna jest równa 2,6.
Wiadomo, że mediana liczb 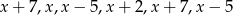 jest równa średniej tych liczb. Zatem liczba
jest równa średniej tych liczb. Zatem liczba 
A) jest równa 3 B) jest równa 4 C) jest równa 5 D) może mieć dowolną wartość
Wiadomo, że mediana liczb 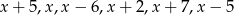 jest dwa razy większa od średniej tych liczb. Zatem liczba
jest dwa razy większa od średniej tych liczb. Zatem liczba 
A) jest równa 0 B) jest równa 1 C) jest równa 2 D) może mieć dowolną wartość
Na diagramie przestawiono wzrost pięciorga uczniów.
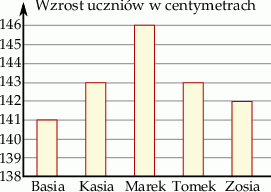
Odchylenie standardowe zestawu danych jest równe
A) 2 cm B) 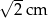 C)
C) 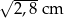 D) 2,8 cm
D) 2,8 cm
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
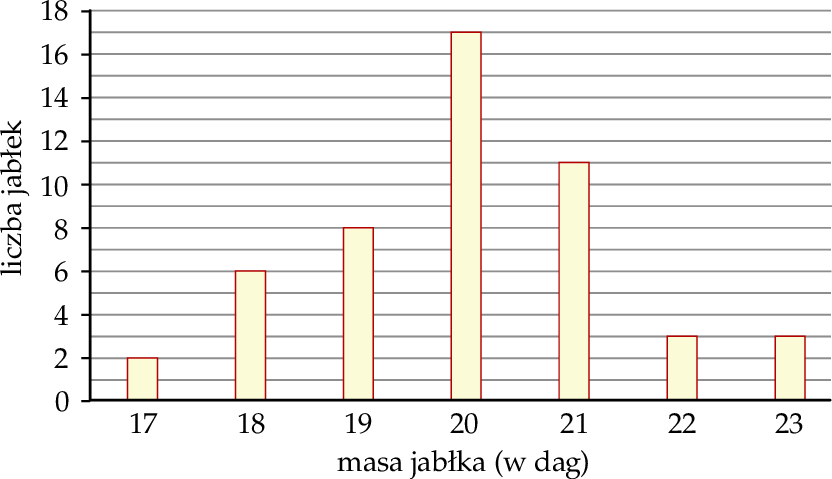
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Dominanta masy tych jabłek z danej próby, które nie spełniają normy jakości, jest większa od 20 dag. | P | F |
| Mediana masy 50 zważonych jabłek jest równa 20 dag. | P | F |
W tabeli poniżej przedstawione są wyniki pracy klasowej.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 3 | 7 | 6 | 9 | 2 | 0 |
Wariancja ocen w tej klasie jest równa
A) 3 B) 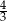 C) 4 D)
C) 4 D) 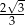
Odchylenie standardowe zestawu danych: 1, 2, 3, 4, 5 jest równe
A) 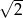 B) 2 C)
B) 2 C) 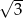 D) 3
D) 3
Odchylenie standardowe zestawu danych: 2, 3, 4, 5, 6 jest równe
A) 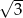 B) 2 C)
B) 2 C) 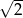 D) 4
D) 4
Odchylenie standardowe zestawu danych: 1, 3, 5, 7 jest równe
A) 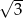 B) 3 C)
B) 3 C) 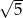 D) 5
D) 5
Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich pracowników pewnej firmy za luty 2024 roku.
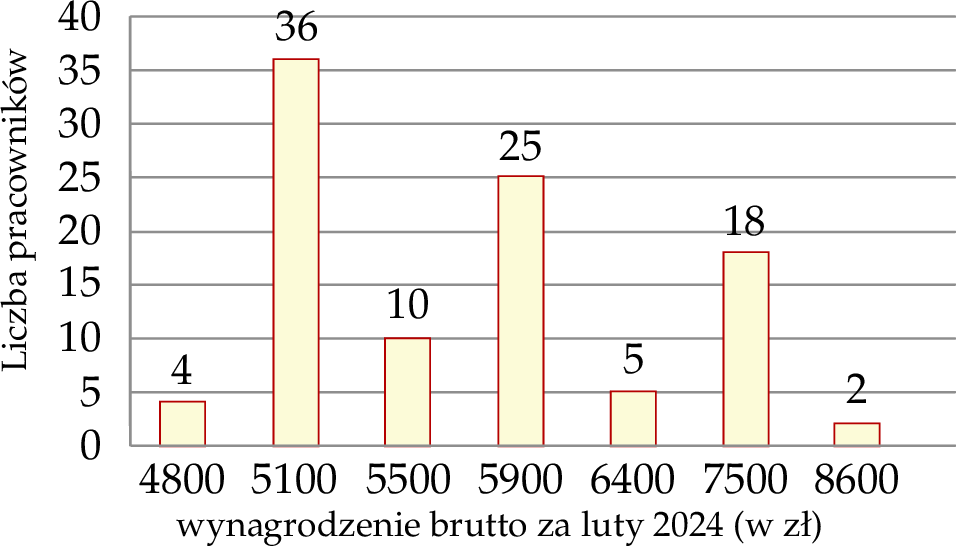
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Zarobki ponad połowy pracowników tej firmy są wyższe od średniej. | P | F |
| Mediana przedstawionych zarobków jest równa 5900 zł. | P | F |
W hurtowni owoców wyselekcjonowane jabłko spełnia normę jakości, gdy jego masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [19 dag, 21 dag]. Pobrano próbę kontrolną liczącą 50 jabłek i następnie zważono każde z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy jabłek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę jabłka (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę jabłek o określonej masie.
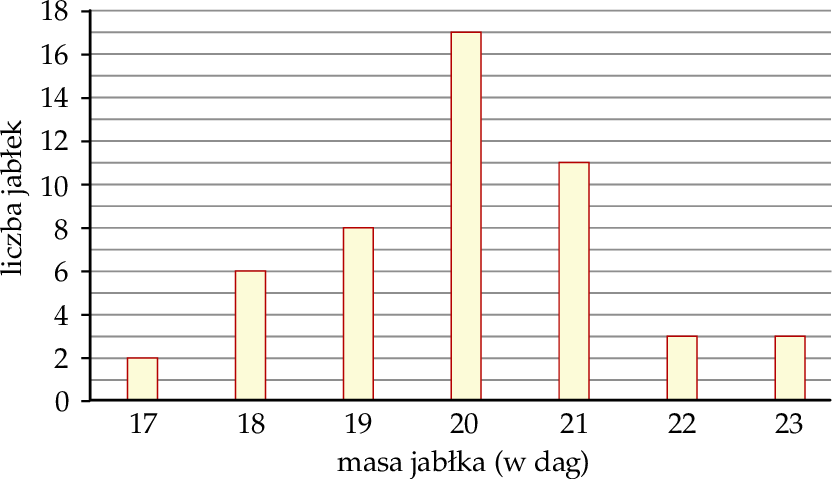
Dominanta masy 50 zważonych jabłek (w zaokrągleniu do pełnych dekagramów) z pobranej próby kontrolnej jest równa
| A) 20 dag, | B) 23 dag, |
ponieważ
| 1) | ta masa jest największa w tej próbie. |
| 2) | iloczyn tej masy i liczby jabłek o takiej masie jest największy w tej próbie. |
| 3) | ta masa występuje najliczniej w tej próbie. |
Na wykresie słupkowym poniżej podano rozkład miesięcznych zarobków wszystkich pracowników w pewnej firmie  . Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy
. Na osi poziomej podano – wyrażone w tysiącach złotych – miesięczne wynagrodzenie netto pracowników firmy  , a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
, a na osi pionowej przedstawiono liczbę osób, która osiąga podane zarobki.
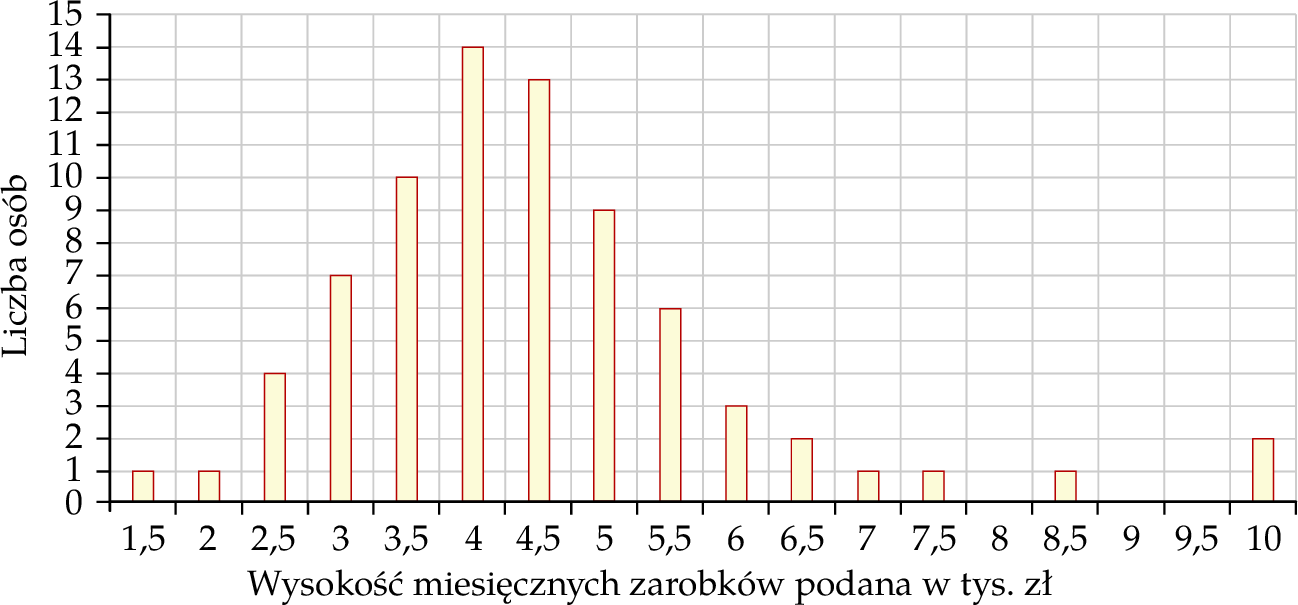
Dominantą miesięcznych zarobków w firmie  jest
jest
| A) 10 tys. zł, | B) 4,5 tys. zł, | C) 4 tys. zł, |
ponieważ
| 1) | tę wartość zarobków osiąga najwięcej osób w firmie  . . |
| 2) | ta wartość zarobków jest największa w firmie  . . |
| 3) | iloczyn tej wartości zarobków i liczby osób z takimi zarobkami jest największy w firmie  . . |
W hurtowni owoców wyselekcjonowana gruszka spełnia normę jakości, gdy jej masa (po zaokrągleniu do pełnych dekagramów) mieści się w przedziale [16 dag, 18 dag]. Pobrano próbę kontrolną liczącą 50 gruszek i następnie zważono każdą z nich. Na poniższym wykresie słupkowym przedstawiono rozkład masy gruszek w badanej próbie. Na osi poziomej podano – wyrażoną w dekagramach – masę gruszki (w zaokrągleniu do pełnych dekagramów), a na osi pionowej przedstawiono liczbę gruszek o określonej masie.
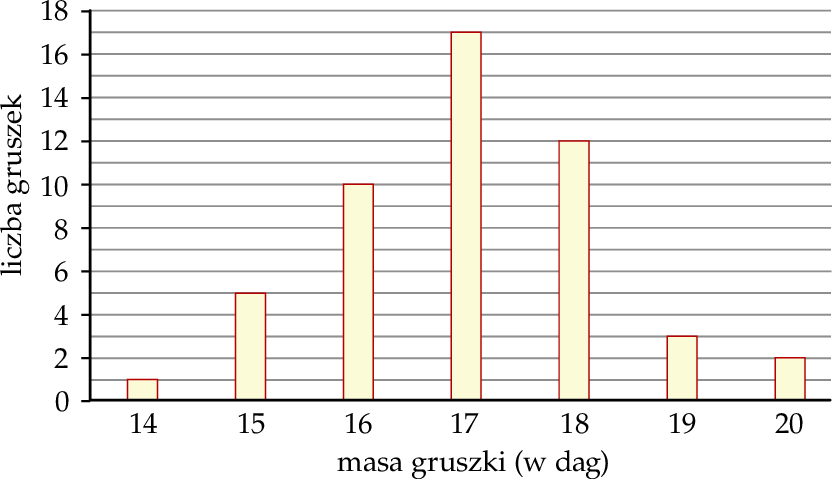
Dominanta masy 50 zważonych gruszek (w zaokrągleniu do pełnych dekagramów) z pobranej próby kontrolnej jest równa
| A) 18 dag, | B) 17 dag, |
ponieważ
| 1) | ta masa jest największa w tej próbie. |
| 3) | ta masa występuje najliczniej w tej próbie. |
| 3) | iloczyn tej masy i liczby gruszek o takiej masie jest największy w tej próbie. |
W zestawie 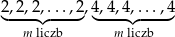 jest
jest 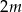 liczb (
liczb (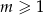 ), w tym
), w tym 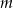 liczb 2 i
liczb 2 i 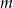 liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
A) 2 B) 1 C) 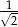 D)
D) 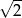
W zestawie 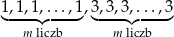 jest
jest 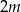 liczb (
liczb (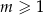 ), w tym
), w tym 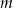 liczb 1 i
liczb 1 i 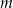 liczb 3. Odchylenie standardowe tego zestawu liczb jest równe
liczb 3. Odchylenie standardowe tego zestawu liczb jest równe
A) 1 B) 2 C) 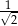 D)
D) 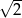
W zestawie 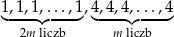 jest
jest 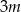 liczb (
liczb (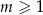 ), w tym
), w tym 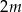 liczb 1 i
liczb 1 i 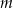 liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
liczb 4. Odchylenie standardowe tego zestawu liczb jest równe
A) 2 B) 1 C) 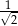 D)
D) 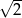
Wykonano pomiary wysokości czterech krzeseł i każde dwa rezultaty były różne. Adam zapisał wyniki w metrach i odchylenie standardowe jego danych było równe 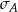 . Bogdan zapisał te same wyniki w centymetrach i odchylenie standardowe jego danych było równe
. Bogdan zapisał te same wyniki w centymetrach i odchylenie standardowe jego danych było równe 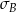 . Wynika stąd, że
. Wynika stąd, że
A) 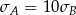 B)
B) 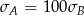 C)
C) 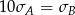 D)
D) 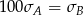
Wykonano pomiary wagi pięciu arbuzów i każde dwa rezultaty były różne. Agata zapisała wyniki w kilogramach i odchylenie standardowe jej danych było równe 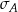 . Basia zapisała te same wyniki w gramach i odchylenie standardowe jej danych było równe
. Basia zapisała te same wyniki w gramach i odchylenie standardowe jej danych było równe 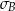 . Wynika stąd, że
. Wynika stąd, że
A) 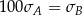 B)
B) 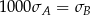 C)
C) 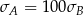 D)
D) 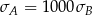
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
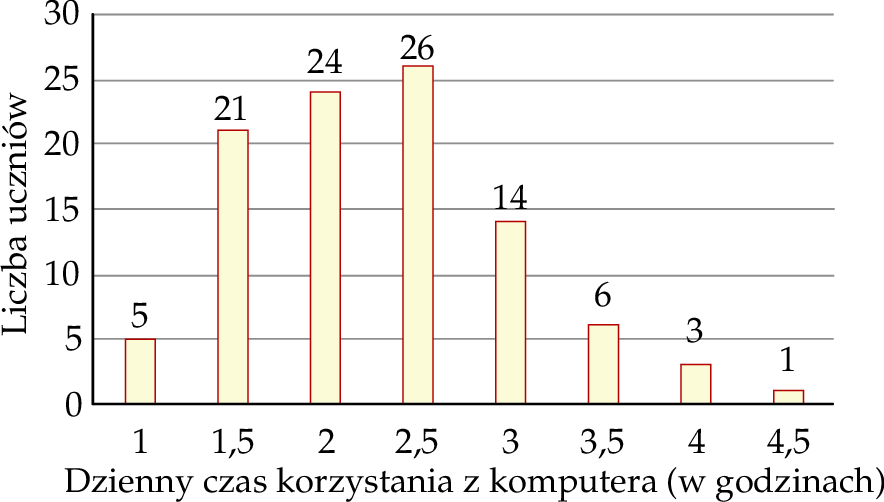
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 2,75 godziny D) 1,50 godziny
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
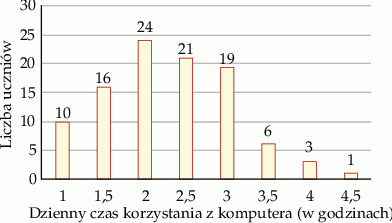
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 1,5 godziny D) 2 godziny
