W kąt o mierze  wpisano ciąg kół w taki sposób, że pierwsze koło ma promień
wpisano ciąg kół w taki sposób, że pierwsze koło ma promień  i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
i jest styczne do ramion kąta a każde następne koło ma mniejszy promień i jest styczne do poprzedniego koła oraz do ramion kąta. Oblicz sumę pól kół tego ciągu.
/Szkoła średnia/Ciągi/Szereg geometryczny
Dany jest nieskończony ciąg geometryczny 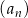 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 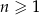 . Czwarty wyraz tego ciągu jest o
. Czwarty wyraz tego ciągu jest o  większy od drugiego wyrazu i jest mniejszy niż trzeci wyraz. Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa
większy od drugiego wyrazu i jest mniejszy niż trzeci wyraz. Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa 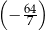 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
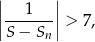
gdzie 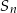 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 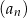 , a
, a 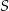 jest sumą wszystkich wszystkich wyrazów ciągu
jest sumą wszystkich wszystkich wyrazów ciągu 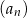 .
.
Dany jest nieskończony ciąg geometryczny 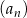 określony dla
określony dla 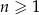 , w którym
, w którym 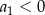 . Suma
. Suma 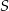 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 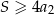 . Wyznacz iloraz tego ciągu.
. Wyznacz iloraz tego ciągu.
Konstruujemy ciąg trójkątów równobocznych 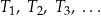 następująco:
następująco:
-
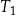 jest trójkątem równobocznym o polu 1.
jest trójkątem równobocznym o polu 1. -
dla każdego
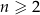 , trójkąt
, trójkąt 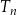 ma wierzchołki na trzech różnych bokach trójkąta
ma wierzchołki na trzech różnych bokach trójkąta 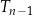 i każdy z wierzchołków trójkąta
i każdy z wierzchołków trójkąta 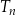 dzieli odpowiedni bok trójkąta
dzieli odpowiedni bok trójkąta 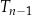 w stosunku 1 : 2.
w stosunku 1 : 2.
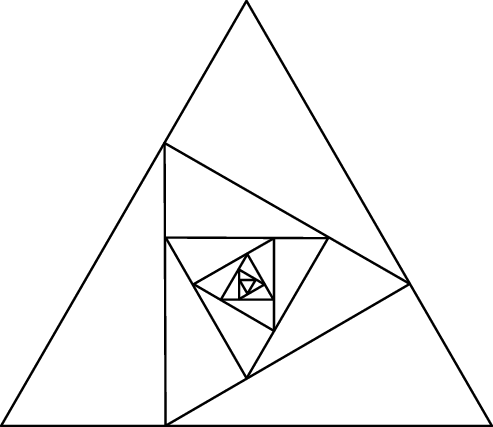
Oblicz sumę pól wszystkich trójkątów 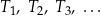 .
.
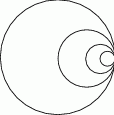
Dane jest koło o promieniu  . W tym kole narysowano koło styczne wewnętrznie o średnicy
. W tym kole narysowano koło styczne wewnętrznie o średnicy  , w narysowanym kole znów narysowano koło styczne wewnętrznie o średnicy
, w narysowanym kole znów narysowano koło styczne wewnętrznie o średnicy 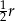 itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich narysowanych kół.
itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich narysowanych kół.
Liczby 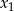 i
i 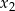 są pierwiastkami równania
są pierwiastkami równania 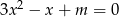 , gdzie
, gdzie 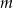 jest pewną ujemną liczbą rzeczywistą. Ciąg
jest pewną ujemną liczbą rzeczywistą. Ciąg 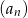 określony jest wzorem
określony jest wzorem 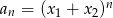 . Oblicz sumę wyrazów tego ciągu.
. Oblicz sumę wyrazów tego ciągu.
Wartości funkcji 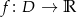 spełniają dla każdego
spełniają dla każdego 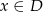 następujące równanie
następujące równanie
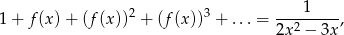
gdzie lewa strona równania jest sumą szeregu geometrycznego.
- Wyznacz dziedzinę i wzór funkcji
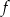 .
. - Naszkicuj wykres funkcji
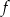 .
.
Dany jest nieskończony ciąg geometryczny 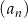 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 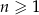 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 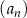 jest równa 7, a suma
jest równa 7, a suma 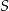 wszystkich wyrazów tego ciągu jest równa 8. Wyznacz wszystkie wartości
wszystkich wyrazów tego ciągu jest równa 8. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
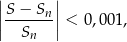
gdzie 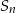 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 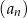 .
.
Dany jest nieskończony ciąg geometryczny 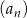 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 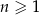 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 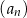 jest równa 26, a suma
jest równa 26, a suma 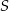 wszystkich wyrazów tego ciągu jest równa 27. Wyznacz wszystkie wartości
wszystkich wyrazów tego ciągu jest równa 27. Wyznacz wszystkie wartości  , dla których spełniona jest nierówność
, dla których spełniona jest nierówność
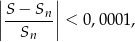
gdzie 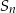 oznacza sumę
oznacza sumę  początkowych wyrazów ciągu
początkowych wyrazów ciągu 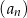 .
.
Oblicz sumę nieskończonego szeregu geometrycznego
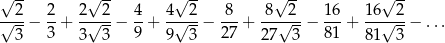
Oblicz sumę nieskończonego szeregu geometrycznego
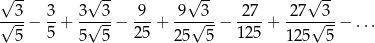
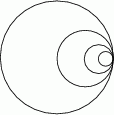
Dany jest okrąg 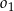 o promieniu
o promieniu  . Wewnątrz tego okręgu narysowano okrąg
. Wewnątrz tego okręgu narysowano okrąg 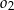 styczny wewnętrznie o średnicy
styczny wewnętrznie o średnicy  , wewnątrz okręgu
, wewnątrz okręgu 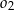 znów narysowano okrąg styczny wewnętrznie o średnicy
znów narysowano okrąg styczny wewnętrznie o średnicy 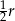 itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów
itd. Czynność tę powtórzono nieskończenie wiele razy. Wykaż, że suma długości okręgów 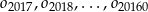 jest mniejsza od długości okręgu
jest mniejsza od długości okręgu 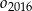 .
.
Nieskończony ciąg geometryczny 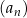 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 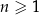 . Suma wszystkich wyrazów ciągu
. Suma wszystkich wyrazów ciągu 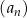 o numerach nieparzystych jest równa 16, tj.
o numerach nieparzystych jest równa 16, tj.
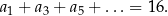
Ponadto 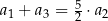 . Wyznacz wzór ogólny na n–ty wyraz ciągu
. Wyznacz wzór ogólny na n–ty wyraz ciągu 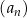 .
.
Rozważmy ciąg trójkątów równobocznych takich, że długość boku pierwszego trójkąta jest równa  , zaś bok każdego następnego jest równy połowie wysokości poprzedniego. Oblicz sumę wszystkich pól tak utworzonych trójkątów.
, zaś bok każdego następnego jest równy połowie wysokości poprzedniego. Oblicz sumę wszystkich pól tak utworzonych trójkątów.
Wyznacz te wartości  , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego
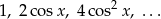
Ciąg 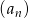 jest określony dla
jest określony dla 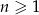 i spełnia warunek
i spełnia warunek
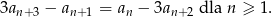
Oblicz sumę dwóch początkowych wyrazów ciągu 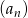 jeżeli suma wszystkich jego wyrazów jest równa 2016.
jeżeli suma wszystkich jego wyrazów jest równa 2016.
Dany jest nieskończony ciąg okręgów 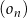 o równaniach
o równaniach 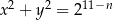 ,
, 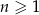 . Niech
. Niech 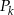 będzie pierścieniem ograniczonym zewnętrznym okręgiem
będzie pierścieniem ograniczonym zewnętrznym okręgiem 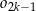 i wewnętrznym okręgiem
i wewnętrznym okręgiem 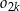 . Oblicz sumę pól wszystkich pierścieni
. Oblicz sumę pól wszystkich pierścieni 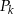 , gdzie
, gdzie 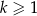 .
.
Dany jest nieskończony ciąg okręgów 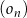 o równaniach
o równaniach 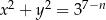 ,
, 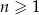 . Niech
. Niech 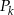 będzie pierścieniem ograniczonym zewnętrznym okręgiem
będzie pierścieniem ograniczonym zewnętrznym okręgiem 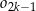 i wewnętrznym okręgiem
i wewnętrznym okręgiem 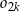 . Oblicz sumę pól wszystkich pierścieni
. Oblicz sumę pól wszystkich pierścieni 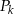 , gdzie
, gdzie 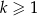 .
.
Określamy kwadraty 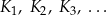 następująco:
następująco:
-
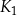 jest kwadratem o boku długości
jest kwadratem o boku długości 
-
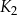 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 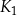 i dzieli ten bok w stosunku 1 : 3
i dzieli ten bok w stosunku 1 : 3 -
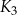 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 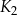 i dzieli ten bok w stosunku 1 : 3
i dzieli ten bok w stosunku 1 : 3
i ogólnie, dla każdej liczby naturalnej 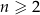 ,
,
-
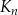 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 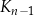 i dzieli ten bok w stosunku 1 : 3.
i dzieli ten bok w stosunku 1 : 3.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
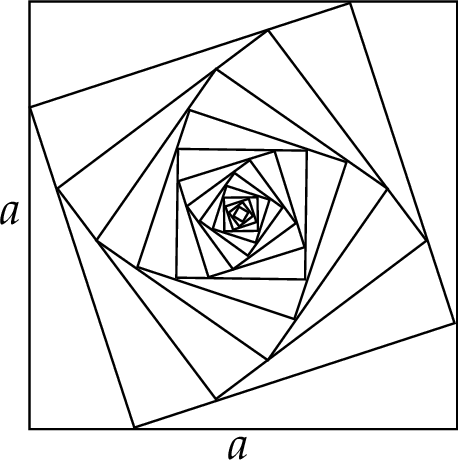
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Określamy kwadraty 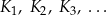 następująco:
następująco:
-
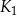 jest kwadratem o boku długości
jest kwadratem o boku długości 
-
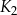 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 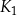 i dzieli ten bok w stosunku 1 : 2
i dzieli ten bok w stosunku 1 : 2 -
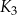 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 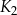 i dzieli ten bok w stosunku 1 : 2
i dzieli ten bok w stosunku 1 : 2
i ogólnie, dla każdej liczby naturalnej 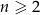 ,
,
-
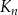 jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu
jest kwadratem, którego każdy wierzchołek leży na innym boku kwadratu 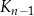 i dzieli ten bok w stosunku 1 : 2.
i dzieli ten bok w stosunku 1 : 2.
Obwody wszystkich kwadratów określonych powyżej tworzą nieskończony ciąg geometryczny. Na rysunku przedstawiono kwadraty utworzone w sposób opisany powyżej.
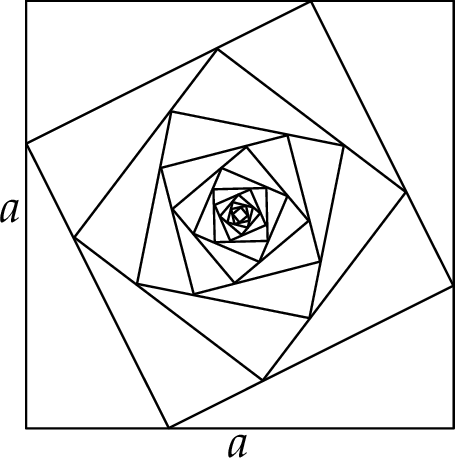
Oblicz sumę wszystkich wyrazów tego nieskończonego ciągu.
Dany jest ciąg 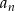 o wyrazie ogólnym
o wyrazie ogólnym 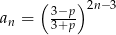 .
.
- Udowodnij, że ciąg
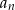 jest ciągiem geometrycznym.
jest ciągiem geometrycznym. - Wyznacz te wartości parametru
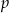 , dla których istnieje suma wszystkich wyrazów ciągu
, dla których istnieje suma wszystkich wyrazów ciągu 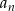 . Oblicz tę sumę.
. Oblicz tę sumę. - Wyznacz te wartości parametru
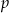 , dla których ciąg
, dla których ciąg 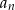 jest malejący.
jest malejący.
W kwadrat o boku  wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę pól wszystkich tych kwadratów.
wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę pól wszystkich tych kwadratów.
W kwadrat o boku  wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę obwodów wszystkich tych kwadratów.
wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę obwodów wszystkich tych kwadratów.
W kwadrat 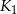 o boku
o boku  wpisujemy kwadrat
wpisujemy kwadrat 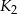 , którego wierzchołki są środkami boków kwadratu
, którego wierzchołki są środkami boków kwadratu 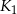 , następnie w kwadrat
, następnie w kwadrat 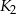 wpisujemy kwadrat
wpisujemy kwadrat 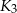 , którego wierzchołki są środkami boków
, którego wierzchołki są środkami boków 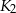 i tak dalej. Oblicz sumę pól otrzymanego w ten sposób nieskończonego ciągu kwadratów.
i tak dalej. Oblicz sumę pól otrzymanego w ten sposób nieskończonego ciągu kwadratów.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 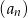 wynosi 124, a suma wszystkich wyrazów tego ciągu równa się 125.
wynosi 124, a suma wszystkich wyrazów tego ciągu równa się 125.
- Oblicz pierwszy wyraz i iloraz ciągu geometrycznego
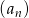 .
. - Sprawdź czy istnieje takie
 , dla którego
, dla którego ![2√2[(1+ √2)2−3] an = 5(√3+-1)(√-3−-1)](https://img.zadania.info/zad/7172985/HzadT3x.gif) .
. - Jakie dwie liczby
 i
i 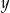 należy wstawić między pierwszy i trzeci wyraz ciągu
należy wstawić między pierwszy i trzeci wyraz ciągu 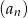 , aby ciąg
, aby ciąg 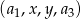 był ciągiem arytmetycznym?
był ciągiem arytmetycznym?
Dany jest nieskończony ciąg sześcianów 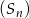 określony dla
określony dla 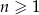 . Krawędź pierwszego z nich jest równa
. Krawędź pierwszego z nich jest równa 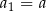 . Krawędź drugiego z tych sześcianów ma długość
. Krawędź drugiego z tych sześcianów ma długość 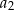 równą różnicy długości przekątnej i przekątnej ściany pierwszego sześcianu. Analogicznie, trzeci sześcian ma krawędź
równą różnicy długości przekątnej i przekątnej ściany pierwszego sześcianu. Analogicznie, trzeci sześcian ma krawędź 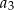 o długości równej różnicy długości przekątnej i przekątnej ściany drugiego sześcianu, itd. Oblicz sumę pól powierzchni wszystkich sześcianów tworzących ciąg
o długości równej różnicy długości przekątnej i przekątnej ściany drugiego sześcianu, itd. Oblicz sumę pól powierzchni wszystkich sześcianów tworzących ciąg 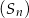 .
.

