W nieskończonym malejącym ciągu geometrycznym 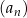 , określonym dla
, określonym dla 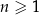 , jest spełniony warunek
, jest spełniony warunek
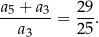
Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa 6. Wyznacz wzór ogólny na  -ty wyraz ciągu
-ty wyraz ciągu 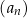 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W nieskończonym malejącym ciągu geometrycznym 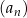 , określonym dla
, określonym dla 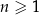 , jest spełniony warunek
, jest spełniony warunek
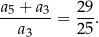
Suma wszystkich wyrazów tego ciągu o numerach parzystych jest równa 6. Wyznacz wzór ogólny na  -ty wyraz ciągu
-ty wyraz ciągu 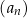 .
.
W trójkąt równoboczny o boku długości  wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
W trójkąt równoboczny o boku długości 3 wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
Dany jest ciąg geometryczny 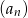 określony wzorem
określony wzorem 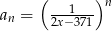 dla
dla 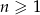 . Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą
. Wszystkie wyrazy tego ciągu są dodatnie. Wyznacz najmniejszą liczbę całkowitą  , dla której nieskończony szereg
, dla której nieskończony szereg 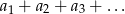 jest zbieżny.
jest zbieżny.
Dany jest ciąg geometryczny 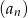 określony wzorem
określony wzorem 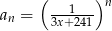 dla
dla 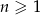 , którego niektóre wyrazy są ujemne. Wyznacz największą liczbę całkowitą
, którego niektóre wyrazy są ujemne. Wyznacz największą liczbę całkowitą  , dla której nieskończony szereg
, dla której nieskończony szereg 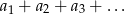 jest zbieżny.
jest zbieżny.
Rozważamy nieskończone ciągi geometryczne o ilorazie 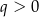 , w których kwadrat drugiego wyrazu jest dodatni i równy sumie wyrazów: drugiego, trzeciego i czwartego. Wyznacz pierwszy wyraz i iloraz tego spośród rozpatrywanych ciągów, którego suma wszystkich wyrazów jest najmniejsza. Oblicz tę sumę.
, w których kwadrat drugiego wyrazu jest dodatni i równy sumie wyrazów: drugiego, trzeciego i czwartego. Wyznacz pierwszy wyraz i iloraz tego spośród rozpatrywanych ciągów, którego suma wszystkich wyrazów jest najmniejsza. Oblicz tę sumę.
Na jednym z ramion kąta ostrego o wierzchołku 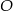 i mierze
i mierze  wybrano punkty
wybrano punkty 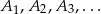 , a na drugim ramieniu punkty
, a na drugim ramieniu punkty 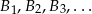 w ten sposób, że
w ten sposób, że 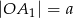 ,
, 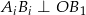 oraz
oraz 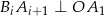 dla wszystkich
dla wszystkich 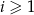 .
.
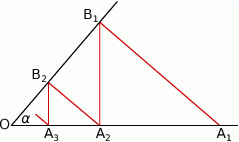
Wykaż, że długość nieskończonej łamanej 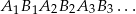 jest równa
jest równa 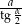 .
.
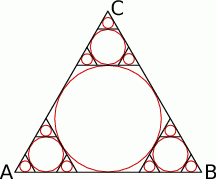
W trójkąt równoboczny 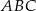 o boku długości 1 wpisano koło. Prowadzimy proste równoległe do boków trójkąta
o boku długości 1 wpisano koło. Prowadzimy proste równoległe do boków trójkąta 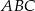 i styczne do koła wpisanego. Proste te odcinają od trójkąta
i styczne do koła wpisanego. Proste te odcinają od trójkąta 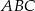 trzy trójkąty równoboczne. W każdy z nich wpisujemy koło i postępujemy analogicznie jak z kołem wpisanym w trójkąt
trzy trójkąty równoboczne. W każdy z nich wpisujemy koło i postępujemy analogicznie jak z kołem wpisanym w trójkąt 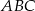 . Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich otrzymanych w ten sposób kół.
. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę pól wszystkich otrzymanych w ten sposób kół.
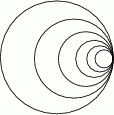
Dane jest koło 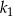 o promieniu
o promieniu  . W tym kole narysowano koło
. W tym kole narysowano koło 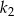 styczne wewnętrznie, którego pole jest równe połowie pola koła
styczne wewnętrznie, którego pole jest równe połowie pola koła 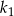 . W kole
. W kole 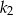 narysowano koło
narysowano koło 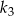 styczne wewnętrznie, którego pole jest równe połowie pola koła
styczne wewnętrznie, którego pole jest równe połowie pola koła 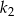 . Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę obwodów wszystkich narysowanych kół.
. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę obwodów wszystkich narysowanych kół.
Dany jest nieskończony ciąg geometryczny 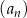 określony dla
określony dla 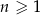 , którego wyrazy są niezerowe i iloraz
, którego wyrazy są niezerowe i iloraz 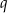 spełnia warunek:
spełnia warunek: 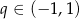 . Suma
. Suma 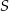 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 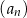 , suma
, suma 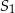 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 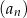 o numerach nieparzystych oraz suma
o numerach nieparzystych oraz suma 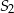 wszystkich wyrazów ciągu
wszystkich wyrazów ciągu 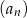 o numerach parzystych są kolejnymi wyrazami ciągu geometrycznego. Oblicz
o numerach parzystych są kolejnymi wyrazami ciągu geometrycznego. Oblicz 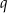 .
.
Dany jest nieskończony ciąg geometryczny 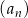 , określony dla każdej liczby naturalnej
, określony dla każdej liczby naturalnej 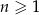 , którego iloraz
, którego iloraz 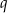 jest równy pierwszemu wyrazowi i spełnia warunek
jest równy pierwszemu wyrazowi i spełnia warunek 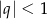 . Stosunek sumy
. Stosunek sumy 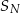 wszystkich wyrazów tego ciągu o numerach nieparzystych do sumy
wszystkich wyrazów tego ciągu o numerach nieparzystych do sumy 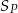 wszystkich wyrazów tego ciągu o numerach parzystych jest równy różnicy tych sum, tj.
wszystkich wyrazów tego ciągu o numerach parzystych jest równy różnicy tych sum, tj. 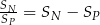 . Oblicz
. Oblicz 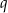 .
.
Wykaż, że zbiór 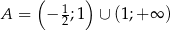 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
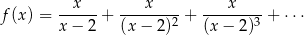
Dany jest nieskończony ciąg geometryczny 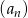 określony dla
określony dla 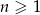 , w którym pierwszy wyraz jest liczbą naturalną, a iloczyn pierwszego i trzeciego wyrazu jest równy 1. Suma wszystkich wyrazów tego ciągu jest liczbą z przedziału
, w którym pierwszy wyraz jest liczbą naturalną, a iloczyn pierwszego i trzeciego wyrazu jest równy 1. Suma wszystkich wyrazów tego ciągu jest liczbą z przedziału 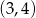 . Oblicz iloraz tego ciągu.
. Oblicz iloraz tego ciągu.
Dany jest nieskończony ciąg geometryczny 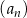 określony dla
określony dla 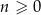 , którego iloraz jest równy
, którego iloraz jest równy 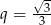 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa 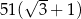 . Oblicz
. Oblicz 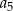 .
.
Wyrazy 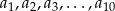 pewnego nieskończonego ciągu
pewnego nieskończonego ciągu 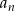 spełniają warunki
spełniają warunki 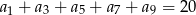 ,
, 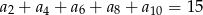 . Wiedząc, że nieskończony ciąg
. Wiedząc, że nieskończony ciąg 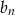 określony wzorem
określony wzorem 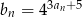 jest ciągiem geometrycznym, oblicz sumę wszystkich wyrazów ciągu
jest ciągiem geometrycznym, oblicz sumę wszystkich wyrazów ciągu 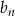 .
.
Niech 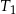 będzie trójkątem równobocznym o boku długości
będzie trójkątem równobocznym o boku długości  . Konstruujemy kolejno trójkąty równoboczne
. Konstruujemy kolejno trójkąty równoboczne 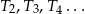 takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól wszystkich tak utworzonych trójkątów
takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól wszystkich tak utworzonych trójkątów 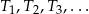 .
.
Wyznacz iloraz nieskończonego, zbieżnego ciągu geometrycznego, w którym pierwszy wyraz jest równy 6, a suma wszystkich wyrazów tego ciągu stanowi  sumy ich kwadratów.
sumy ich kwadratów.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 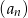 wynosi 6, a suma
wynosi 6, a suma 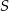 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 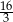 . Oblicz iloraz ciągu
. Oblicz iloraz ciągu 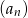 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 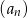 wynosi
wynosi 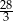 , a suma
, a suma 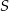 wszystkich wyrazów tego ciągu jest równa 9. Oblicz pierwszy wyraz
wszystkich wyrazów tego ciągu jest równa 9. Oblicz pierwszy wyraz 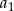 tego ciągu.
tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 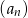 wynosi 18, a suma
wynosi 18, a suma 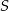 wszystkich wyrazów tego ciągu jest równa 16. Oblicz pierwszy wyraz
wszystkich wyrazów tego ciągu jest równa 16. Oblicz pierwszy wyraz 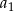 tego ciągu.
tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 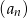 wynosi 14, a suma
wynosi 14, a suma 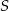 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 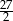 . Oblicz iloraz ciągu
. Oblicz iloraz ciągu 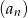 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 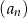 wynosi
wynosi 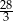 , a suma
, a suma 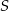 wszystkich wyrazów tego ciągu jest równa 9. Oblicz iloraz ciągu
wszystkich wyrazów tego ciągu jest równa 9. Oblicz iloraz ciągu 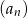 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 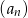 wynosi 6, a suma
wynosi 6, a suma 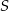 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 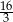 . Oblicz pierwszy wyraz
. Oblicz pierwszy wyraz 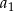 tego ciągu.
tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 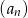 wynosi 14, a suma
wynosi 14, a suma 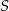 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 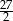 . Oblicz pierwszy wyraz
. Oblicz pierwszy wyraz 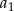 tego ciągu.
tego ciągu.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego 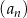 wynosi 18, a suma
wynosi 18, a suma 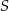 wszystkich wyrazów tego ciągu jest równa 16. Oblicz iloraz tego ciągu.
wszystkich wyrazów tego ciągu jest równa 16. Oblicz iloraz tego ciągu.
Monotoniczny ciąg geometryczny 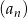 jest zdefiniowany przez warunki
jest zdefiniowany przez warunki
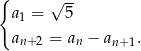
Oblicz sumę wszystkich wyrazów ciągu 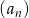 .
.
Niech 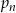 , dla liczby całkowitej
, dla liczby całkowitej 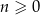 , oznacza sumę odwrotności pierwiastków równania
, oznacza sumę odwrotności pierwiastków równania
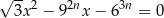
z niewiadomą  . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 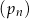 .
.
Ciąg 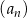 jest określony dla
jest określony dla 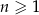 i spełnia warunki
i spełnia warunki
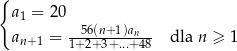
Oblicz granicę
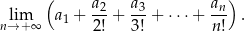
Iloczyn wszystkich wyrazów ciągu danego wzorem
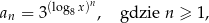
jest równy 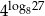 . Oblicz
. Oblicz  .
.
Wykaż, że suma szeregu geometrycznego zbieżnego jest ujemna wtedy i tylko wtedy, gdy jego pierwszy wyraz jest ujemny.
