W zbieżnym nieskończonym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy 4, a różnica między trzecim i piątym wyrazem jest równa 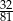 . Jaka jest suma wyrazów tego ciągu?
. Jaka jest suma wyrazów tego ciągu?
/Szkoła średnia/Ciągi/Szereg geometryczny
Ciąg 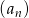 jest określony dla
jest określony dla 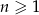 i spełnia warunki
i spełnia warunki
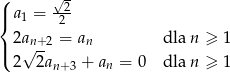
Oblicz granicę
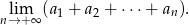
Suma nieskończonego zbieżnego ciągu geometrycznego jest równa 56, a suma kwadratów wyrazów tego ciągu jest równa 448. Znajdź pierwszy wyraz tego ciągu i napisz wzór na wyraz ogólny.
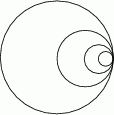
Dany jest okrąg 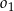 o promieniu
o promieniu  . Wewnątrz tego okręgu narysowano okrąg
. Wewnątrz tego okręgu narysowano okrąg 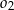 styczny wewnętrznie o średnicy
styczny wewnętrznie o średnicy  , wewnątrz okręgu
, wewnątrz okręgu 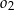 znów narysowano okrąg styczny wewnętrznie o średnicy
znów narysowano okrąg styczny wewnętrznie o średnicy 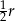 itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę długości wszystkich skonstruowanych w ten sposób okręgów.
itd. Czynność tę powtórzono nieskończenie wiele razy. Oblicz sumę długości wszystkich skonstruowanych w ten sposób okręgów.
Dany jest nieskończony ciąg geometryczny 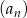 określony dla
określony dla 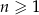 , w którym
, w którym 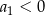 . Suma
. Suma 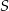 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 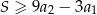 . Wykaż, ze
. Wykaż, ze 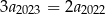 .
.
Wyznacz te wartości  , dla których istnieje suma nieskończonego ciągu geometrycznego
, dla których istnieje suma nieskończonego ciągu geometrycznego
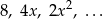
Dany jest nieskończony ciąg geometryczny 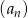 określony dla
określony dla 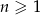 , w którym iloraz jest równy pierwszemu wyrazowi, a suma wszystkich wyrazów tego ciągu jest równa 12. Oblicz pierwszy wyraz tego ciągu.
, w którym iloraz jest równy pierwszemu wyrazowi, a suma wszystkich wyrazów tego ciągu jest równa 12. Oblicz pierwszy wyraz tego ciągu.
Dany jest nieskończony ciąg geometryczny 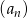 określony dla
określony dla 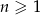 , w którym iloraz jest dwa razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 14. Oblicz pierwszy wyraz tego ciągu.
, w którym iloraz jest dwa razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 14. Oblicz pierwszy wyraz tego ciągu.
Suma czterech początkowych wyrazów ciągu 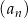 określonego dla
określonego dla 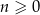 jest równa
jest równa 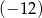 . Ponadto dla każdej liczby całkowitej
. Ponadto dla każdej liczby całkowitej 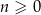 spełniony jest warunek
spełniony jest warunek 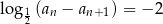 . Oblicz nieskończoną sumę
. Oblicz nieskończoną sumę
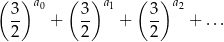
W trójkącie 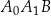 kąt
kąt 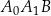 jest prosty,
jest prosty, 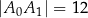 i
i 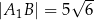 . Odcinek
. Odcinek 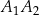 jest wysokością tego trójkąta, odcinek
jest wysokością tego trójkąta, odcinek 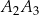 jest wysokością trójkąta
jest wysokością trójkąta 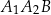 , odcinek
, odcinek 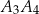 jest wysokością trójkąta
jest wysokością trójkąta 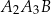 itd. Ogólnie, dla każdej liczby naturalnej
itd. Ogólnie, dla każdej liczby naturalnej 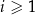 , odcinek
, odcinek 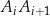 jest wysokością trójkąta
jest wysokością trójkąta 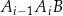
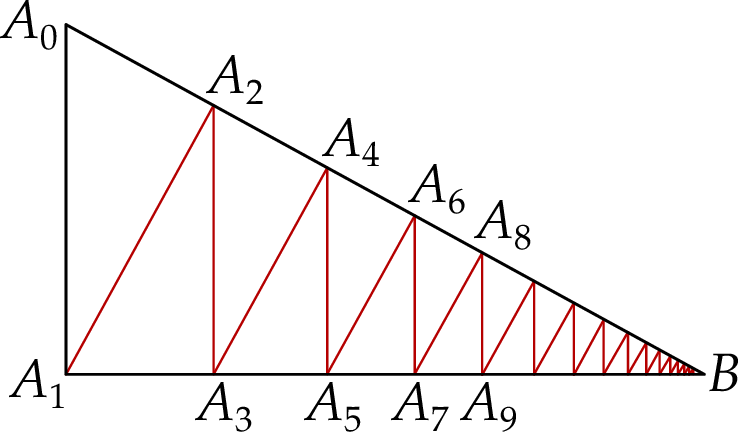
Oblicz długość nieskończonej łamanej 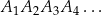 .
.
Oblicz sumę nieskończonego ciągu geometrycznego 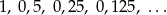
Dany jest nieskończony ciąg geometryczny
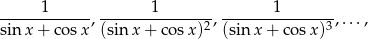
gdzie 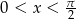 .
.
- Wykaż, że dany ciąg jest malejący.
- Wyznacz sumę
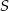 wszystkich wyrazów tego ciągu.
wszystkich wyrazów tego ciągu. - Wiedząc, że suma
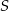 wszystkich wyrazów tego ciągu wynosi
wszystkich wyrazów tego ciągu wynosi 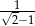 , oblicz
, oblicz  .
.
Suma wszystkich wyrazów nieskończonego ciągu geometrycznego jest równa 3, a suma sześcianów wszystkich jego wyrazów jest równa 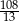 . Oblicz pierwszy wyraz tego ciągu i jego iloraz.
. Oblicz pierwszy wyraz tego ciągu i jego iloraz.
Oblicz sumę szeregu
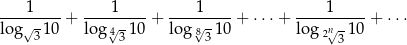
Dany jest nieskończony ciąg geometryczny 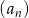 , który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym
, który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym 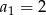 , oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu
, oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu 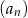 jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
Wyznacz zbiór wartości funkcji
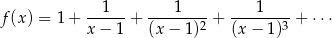
określonej dla wszystkich wartości  , dla których prawa strona powyższego wzoru jest sumą wyrazów zbieżnego szeregu geometrycznego.
, dla których prawa strona powyższego wzoru jest sumą wyrazów zbieżnego szeregu geometrycznego.
Niech 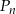 oznacza pole koła o promieniu
oznacza pole koła o promieniu 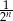 , dla
, dla 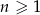 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 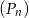 .
.
Niech 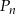 oznacza pole koła o promieniu
oznacza pole koła o promieniu 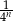 , dla
, dla 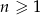 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 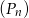 .
.
Niech 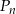 oznacza pole koła o promieniu
oznacza pole koła o promieniu 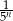 , dla
, dla 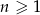 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 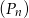 .
.
Niech 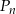 oznacza pole koła o promieniu
oznacza pole koła o promieniu 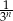 , dla
, dla 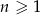 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 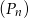 .
.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego wynosi 6, a suma 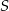 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 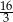 . Dla jakich naturalnych
. Dla jakich naturalnych  spełniona jest nierówność
spełniona jest nierówność 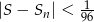 ?
?
Suma wszystkich wyrazów ciągu danego wzorem 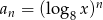 , gdzie
, gdzie 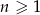 jest równa
jest równa 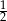 . Oblicz
. Oblicz  .
.
Na płaszczyźnie dany jest nieskończony ciąg 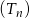 , dla
, dla 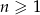 , równoramiennych trójkątów prostokątnych. Pole trójkąta
, równoramiennych trójkątów prostokątnych. Pole trójkąta 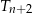 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 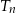 dla
dla 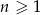 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 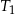 i
i 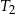 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Na płaszczyźnie dany jest nieskończony ciąg 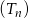 , dla
, dla 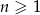 , trójkątów równobocznych. Pole trójkąta
, trójkątów równobocznych. Pole trójkąta 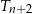 jest dwa razy mniejsze od pola trójkąta
jest dwa razy mniejsze od pola trójkąta 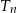 dla
dla 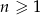 . Uzasadnij, że suma pól trójkątów
. Uzasadnij, że suma pól trójkątów 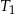 i
i 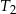 jest równa sumie pól wszystkich pozostałych trójkątów.
jest równa sumie pól wszystkich pozostałych trójkątów.
Dany jest nieskończony ciąg geometryczny 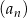 określony dla
określony dla 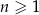 , w którym
, w którym 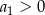 . Suma
. Suma 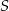 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 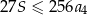 . Wyznacz iloraz tego ciągu.
. Wyznacz iloraz tego ciągu.

