Dana jest funkcja kwadratowa 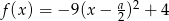
- Dla
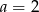 wyznacz postać iloczynową tej funkcji.
wyznacz postać iloczynową tej funkcji. - Dla
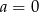 wyznacz te argumenty, dla których funkcja osiąga wartości ujemne.
wyznacz te argumenty, dla których funkcja osiąga wartości ujemne. - Wyznacz
 tak, aby osią symetrii wykresu funkcji była prosta o równaniu
tak, aby osią symetrii wykresu funkcji była prosta o równaniu 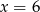 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dana jest funkcja kwadratowa 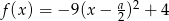
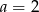 wyznacz postać iloczynową tej funkcji.
wyznacz postać iloczynową tej funkcji. 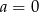 wyznacz te argumenty, dla których funkcja osiąga wartości ujemne.
wyznacz te argumenty, dla których funkcja osiąga wartości ujemne.  tak, aby osią symetrii wykresu funkcji była prosta o równaniu
tak, aby osią symetrii wykresu funkcji była prosta o równaniu 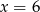 .
.Znajdź taką wartość parametru 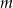 , aby największa wartość funkcji
, aby największa wartość funkcji 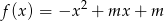 była najmniejsza z możliwych.
była najmniejsza z możliwych.
Dana jest rodzina funkcji kwadratowych zmiennej rzeczywistej  , opisana wzorem
, opisana wzorem 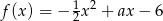 , gdzie
, gdzie  jest liczbą rzeczywistą.
jest liczbą rzeczywistą.
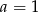 wyznacz zbiór tych argumentów, dla których funkcja
wyznacz zbiór tych argumentów, dla których funkcja 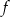 przyjmuje wartości większe niż funkcja liniowa
przyjmuje wartości większe niż funkcja liniowa 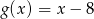 .
.  , dla której zbiorem wartości funkcji
, dla której zbiorem wartości funkcji 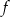 jest przedział
jest przedział 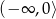 .
. 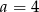 napisz wzór funkcji
napisz wzór funkcji 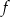 w postaci kanonicznej i narysuj jej wykres.
w postaci kanonicznej i narysuj jej wykres.Funkcja 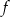 określona jest wzorem
określona jest wzorem 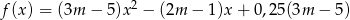 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 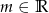 , dla których najmniejsza wartość funkcji
, dla których najmniejsza wartość funkcji 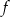 jest liczbą dodatnią.
jest liczbą dodatnią.
Wyznacz wszystkie wartości parametru 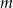 , dla których funkcja
, dla których funkcja 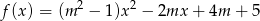 jest rosnąca w przedziale
jest rosnąca w przedziale 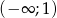 i malejąca w przedziale
i malejąca w przedziale 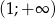 .
.
Liczba 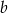 jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji
jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji 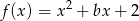 jest większa od
jest większa od 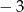 . Wyznacz liczbę
. Wyznacz liczbę 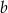 .
.
Wyznacz te wartości parametru 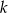 , dla których funkcja
, dla których funkcja 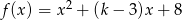 jest malejąca w przedziale
jest malejąca w przedziale 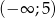 i rosnąca w przedziale
i rosnąca w przedziale 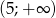 .
.
Funkcja 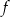 jest określona wzorem
jest określona wzorem 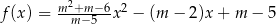 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 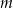 , dla których funkcja
, dla których funkcja 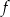 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Funkcja kwadratowa 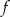 jest określona wzorem
jest określona wzorem 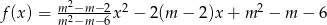 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 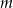 , dla których rozwiązaniem nierówności
, dla których rozwiązaniem nierówności 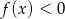 jest przedział postaci
jest przedział postaci 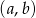 , gdzie
, gdzie 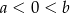 .
.
Funkcja 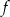 jest określona wzorem
jest określona wzorem 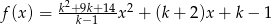 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 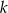 , dla których funkcja
, dla których funkcja 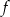 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Funkcja 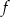 określona wzorem
określona wzorem 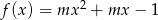 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 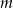 , dla których:
, dla których:
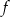 przyjmuje tylko wartości ujemne,
przyjmuje tylko wartości ujemne, 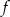 jest przedział
jest przedział 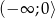 .
.Funkcję kwadratową 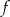 można opisać wzorem mającym postać
można opisać wzorem mającym postać 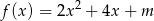 .
.
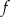 ma dwa różne pierwiastki
ma dwa różne pierwiastki 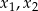 , a następnie oblicz
, a następnie oblicz 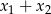 .
. 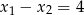 , oblicz
, oblicz 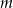 . Dla wyznaczonej liczby
. Dla wyznaczonej liczby 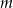 naszkicuj wykres funkcji
naszkicuj wykres funkcji 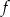 w układzie współrzędnych, a następnie rozwiąż równanie
w układzie współrzędnych, a następnie rozwiąż równanie 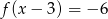 .
. 
Funkcja 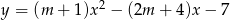 jest malejąca w zbiorze
jest malejąca w zbiorze 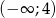 i rosnąca w zbiorze
i rosnąca w zbiorze 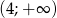 . Wyznacz parametr
. Wyznacz parametr 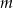 .
.
Dana jest funkcja 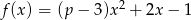 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 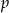 , dla których:
, dla których:
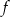 jest liczbą ujemną,
jest liczbą ujemną, 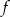 jest mniejsza od -2.
jest mniejsza od -2.Wyznacz wszystkie całkowite wartości 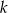 , dla których funkcja
, dla których funkcja 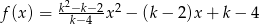 osiąga minimum i ma dwa różne miejsca zerowe.
osiąga minimum i ma dwa różne miejsca zerowe.
