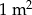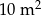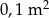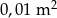W czworokącie 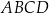 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 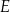 oraz
oraz 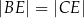 . Przekątna
. Przekątna 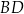 dzieli czworokąt
dzieli czworokąt 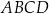 na trójkąt równoboczny i trójkąt równoramienny (zobacz rysunek).
na trójkąt równoboczny i trójkąt równoramienny (zobacz rysunek).
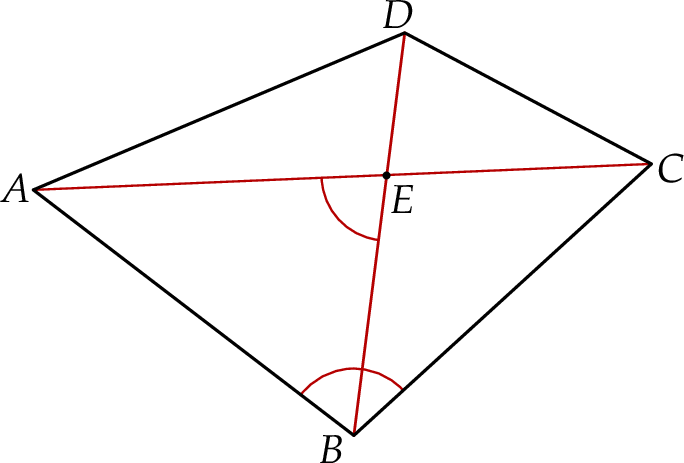
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 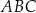 ma miarę ma miarę 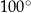 . . | P | F |
Kąt 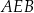 ma miarę ma miarę 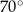 . . | P | F |

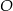 , który jest styczny do wszystkich boków trapezu równoramiennego
, który jest styczny do wszystkich boków trapezu równoramiennego 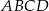 . Ramiona
. Ramiona 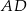 i
i 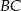 są styczne do tego okręgu odpowiednio w punktach
są styczne do tego okręgu odpowiednio w punktach 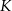 i
i 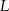 . Kąt wypukły
. Kąt wypukły 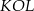 ma miarę
ma miarę 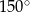 .
. 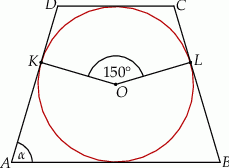
 kąta ostrego tego trapezu jest równa
kąta ostrego tego trapezu jest równa 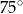
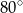
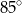
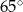
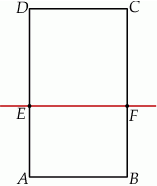
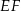 dzieli prostokąt
dzieli prostokąt 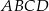 na kwadrat
na kwadrat 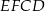 o obwodzie 32 cm i prostokąt
o obwodzie 32 cm i prostokąt 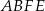 o obwodzie o 6 cm mniejszym od obwodu kwadratu
o obwodzie o 6 cm mniejszym od obwodu kwadratu 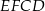 .
. 
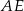 jest równa
jest równa 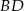 deltoidu przedstawionego na rysunku jest równa
deltoidu przedstawionego na rysunku jest równa 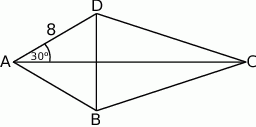
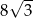
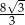
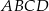 ma środek
ma środek 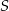 i jest styczny do boków
i jest styczny do boków 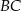 i
i 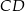 odpowiednio w punktach
odpowiednio w punktach 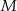 i
i 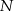 . Kąt
. Kąt 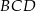 ma miarę
ma miarę 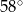 (rysunek).
(rysunek). 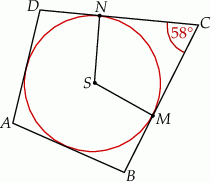
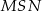 ma miarę
ma miarę 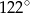
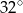
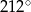
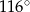
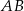 i
i 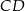 . Dane są długości odcinków
. Dane są długości odcinków 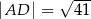 ,
, 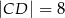 ,
, 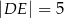 .
. 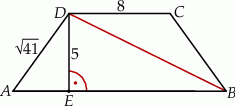
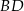 jest równa
jest równa 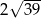
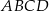 jest wpisany w okrąg, przy czym przekątna
jest wpisany w okrąg, przy czym przekątna 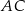 jest średnicą tego okręgu oraz
jest średnicą tego okręgu oraz 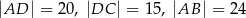 . Wtedy
. Wtedy 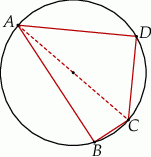
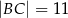
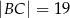
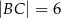
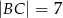
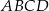 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 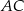 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 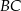 i
i 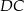 , a kąt
, a kąt 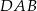 ma miarę
ma miarę 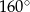 .
. 
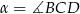 jest równa
jest równa 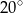
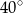
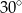
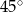
 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 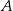 i
i 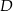 są równe
są równe 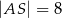 i
i 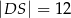 . Bok
. Bok 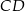 tego czworokąta ma długość
tego czworokąta ma długość 
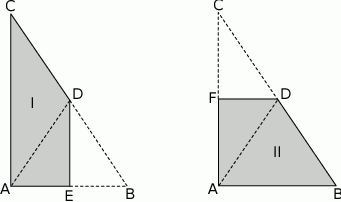
 boki
boki  ,
, 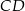 i
i 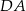 mają równe długości, a kąt
mają równe długości, a kąt 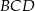 ma miarę
ma miarę 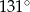 . Przekątna
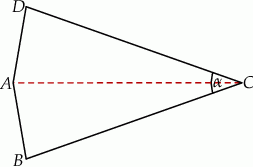
. Przekątna 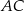 dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek). 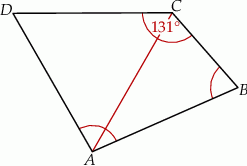
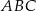 ma miarę
ma miarę 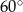 .
.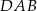 ma miarę
ma miarę 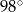 .
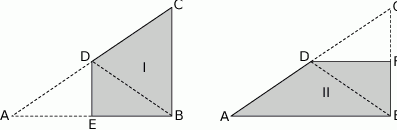
.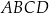 boki
boki 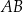 ,
, 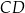 i
i 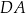 mają równe długości, a kąt
mają równe długości, a kąt 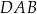 ma miarę
ma miarę 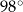 . Przekątna
. Przekątna 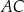 dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek). 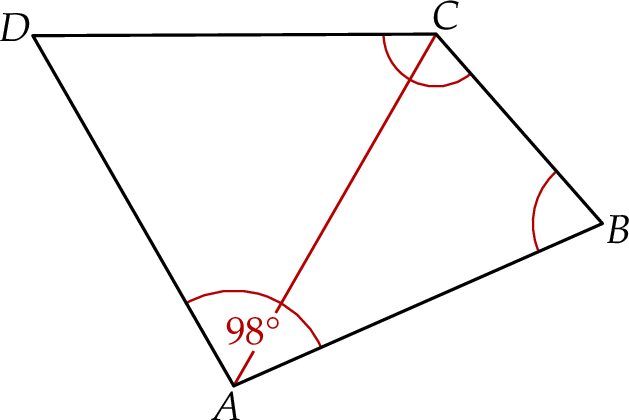
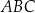 ma miarę
ma miarę 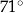 .
.  ma miarę
ma miarę 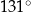 .
.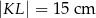 ,
, 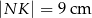 (patrz rysunek).
(patrz rysunek). 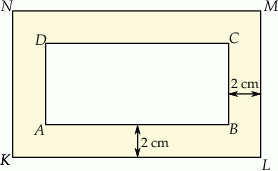
 i
i  są podobne.
są podobne.  jest o 8 cm mniejszy od obwodu prostokąta
jest o 8 cm mniejszy od obwodu prostokąta 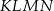 .
. , trzeci ma miarę o
, trzeci ma miarę o 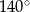 większą niż kąt
większą niż kąt  , a czwarty ma miarę osiem razy większą niż kąt
, a czwarty ma miarę osiem razy większą niż kąt  .
.