Dane są punkty 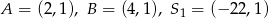 i
i 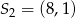 . Odcinek
. Odcinek 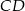 jest obrazem odcinka
jest obrazem odcinka 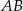 w jednokładności o skali dodatniej i środku
w jednokładności o skali dodatniej i środku 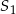 , jak i w jednokładności o skali ujemnej i środku
, jak i w jednokładności o skali ujemnej i środku 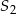 . Oblicz współrzędne punktów
. Oblicz współrzędne punktów 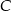 i
i 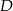 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Przekształcenia/Jednokładność
Końcami odcinka są punkty o współrzędnych 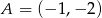 oraz
oraz 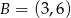 . Odcinek
. Odcinek 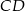 jest obrazem odcinka
jest obrazem odcinka 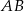 zarówno w jednokładności o dodatniej skali i środku
zarówno w jednokładności o dodatniej skali i środku 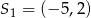 , jak i w jednokładności o ujemnej skali i środku
, jak i w jednokładności o ujemnej skali i środku 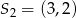 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 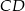 oraz skalę jednokładności o środku
oraz skalę jednokładności o środku 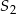 .
.
Kwadrat o wierzchołkach 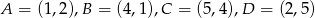 przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach
przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach 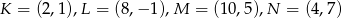 . Wyznacz środek i skalę tej jednokładności.
. Wyznacz środek i skalę tej jednokładności.
Oblicz współrzędne środka 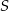 i skalę
i skalę 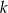 jednokładności, w której obrazem odcinka
jednokładności, w której obrazem odcinka 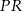 jest odcinek
jest odcinek 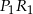 i wiadomo, że
i wiadomo, że 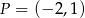 ,
, 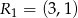 ,
, ![−→ SP 1 = [3,9]](https://img.zadania.info/zad/3303604/HzadT6x.gif) i
i ![−→ SR = [2 ,1]](https://img.zadania.info/zad/3303604/HzadT7x.gif) .
.
Odcinek 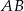 , gdzie
, gdzie 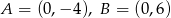 , jest przeciwprostokątną trójkąta prostokątnego
, jest przeciwprostokątną trójkąta prostokątnego 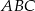 . Wierzchołek
. Wierzchołek 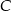 o ujemnej odciętej należy do prostej
o ujemnej odciętej należy do prostej 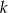 o równaniu
o równaniu 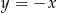 .
.
- Oblicz współrzędne wierzchołka
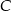 .
. - Obrazem trójkąta
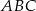 w jednokładności o środku
w jednokładności o środku 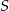 i skali
i skali 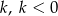 , jest trójkąt
, jest trójkąt 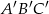 , którego pole wynosi 5. Wiedząc dodatkowo, że
, którego pole wynosi 5. Wiedząc dodatkowo, że 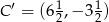 , oblicz skalę jednokładności i współrzędne punktu
, oblicz skalę jednokładności i współrzędne punktu 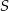 .
.
Obrazem trójkąta 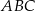 o wierzchołkach
o wierzchołkach 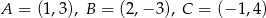 w jednokładności o środku
w jednokładności o środku 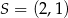 i skali
i skali 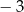 jest trójkąt
jest trójkąt 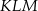 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 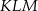 .
.
Obrazem trójkąta 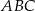 w jednokładności o środku
w jednokładności o środku 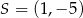 i skali
i skali 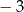 jest trójkąt
jest trójkąt 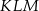 o wierzchołkach
o wierzchołkach 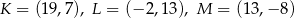 . Wyznacz współrzędne wierzchołków trójkąta
. Wyznacz współrzędne wierzchołków trójkąta 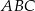 .
.
W jednokładności o środku 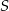 i skali
i skali 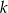 obrazem okręgu o równaniu
obrazem okręgu o równaniu 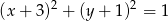 jest okrąg o równaniu
jest okrąg o równaniu 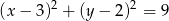 . Oblicz współrzędne środka
. Oblicz współrzędne środka 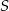 jednokładności.
jednokładności.
W trójkącie 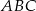 dane są:
dane są: 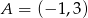 ,
, ![→ AB = [5,− 4]](https://img.zadania.info/zad/4852794/HzadT2x.gif) oraz
oraz ![→ BC = [2,6]](https://img.zadania.info/zad/4852794/HzadT3x.gif) . Trójkąt
. Trójkąt 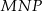 jest obrazem trójkąta
jest obrazem trójkąta 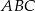 w jednokładności o środku w punkcie
w jednokładności o środku w punkcie 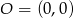 i skali
i skali 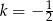 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 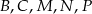 .
.
Wyznacz współrzędne środka okręgu, który jest obrazem okręgu o równaniu 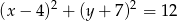 w jednokładności o środku
w jednokładności o środku 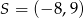 i skali
i skali 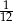 .
.
Trójkąt o wierzchołkach 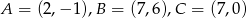 przekształcono w jednokładności o skali
przekształcono w jednokładności o skali 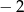 i otrzymano trójkąt o wierzchołkach
i otrzymano trójkąt o wierzchołkach  . Wyznacz współrzędne punktów
. Wyznacz współrzędne punktów 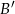 i
i 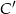 jeżeli
jeżeli 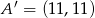 .
.
Dany jest okrąg 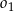 o równaniu
o równaniu 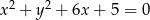 oraz okrąg
oraz okrąg 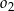 o równaniu
o równaniu 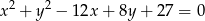 . Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu
. Oblicz współrzędne środka jednokładności i skalę jednokładności, w której obrazem okręgu 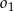 jest okrąg
jest okrąg 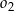 .
.
Prosta o równaniu 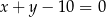 przecina okrąg o równaniu
przecina okrąg o równaniu 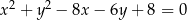 w punktach
w punktach 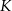 i
i 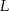 . Punkt
. Punkt 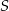 jest środkiem cięciwy
jest środkiem cięciwy 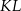 . Wyznacz równanie obrazu tego okręgu w jednokładności o środku
. Wyznacz równanie obrazu tego okręgu w jednokładności o środku 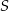 i skali
i skali 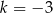 .
.
Wyznacz równanie okręgu, który jest obrazem okręgu 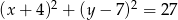 w jednokładności o środku
w jednokładności o środku 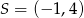 i skali
i skali 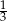 .
.
Wyznacz równanie okręgu, który jest obrazem okręgu 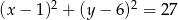 w jednokładności o środku
w jednokładności o środku 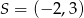 i skali
i skali 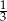 .
.
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu 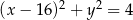 jest okrąg o równaniu
jest okrąg o równaniu 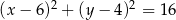 , a skala tej jednokładności jest liczbą ujemną.
, a skala tej jednokładności jest liczbą ujemną.

