Wielomian 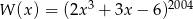 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 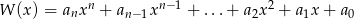 . Oblicz sumę
. Oblicz sumę 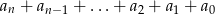 .
.
/Szkoła średnia/Funkcje
Niech 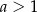 będzie ustaloną liczbą rzeczywistą i
będzie ustaloną liczbą rzeczywistą i 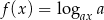 .
.
- Wyznacz dziedzinę funkcji
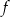 .
. - Oblicz
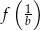 jeżeli
jeżeli 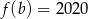 .
.
Oblicz 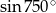 .
.
Oblicz 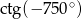 .
.
Oblicz 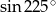 .
.
Oblicz 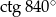 .
.
Oblicz 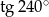 .
.
Oblicz 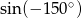 .
.
Oblicz 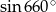 .
.
Oblicz 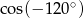 .
.
Oblicz 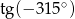 .
.
Kąt  jest ostry i
jest ostry i 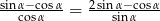 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia 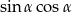 .
.
Niech ciąg 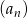 , dla
, dla 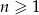 , będzie resztą z dzielenia wielomianu
, będzie resztą z dzielenia wielomianu 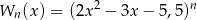 przez dwumian
przez dwumian 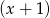 . Oblicz sumę dziesięciu początkowych wyrazów ciągu
. Oblicz sumę dziesięciu początkowych wyrazów ciągu 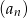 .
.
Wyznacz te argumenty, dla których funkcja 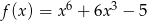 osiąga wartość najmniejszą.
osiąga wartość najmniejszą.
Wykaż, że

Wykaż, że
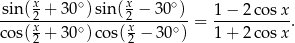
Reszta z dzielenia wielomianu 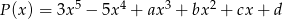 przez wielomian
przez wielomian 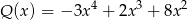 jest taka sama jak reszta z dzielenia wielomianu
jest taka sama jak reszta z dzielenia wielomianu 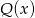 przez wielomian
przez wielomian 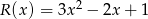 . Oblicz wartości współczynników
. Oblicz wartości współczynników 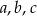 i
i 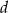 .
.
Dla jakich wartości parametru 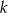 dziedziną funkcji
dziedziną funkcji 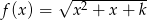 jest zbiór liczb rzeczywistych?
jest zbiór liczb rzeczywistych?
Reszta z dzielenia wielomianu 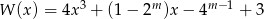 przez dwumian
przez dwumian 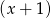 jest równa -2.
jest równa -2.
- Wyznacz wartość parametru
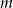 .
. - Dla wyznaczonej wartości parametru
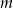 rozwiąż nierówność
rozwiąż nierówność 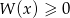 .
.
Kąt  jest ostry i
jest ostry i 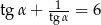 oblicz
oblicz 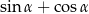 .
.
Wyznacz dziedzinę funkcji
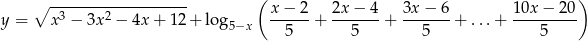
Wielomian 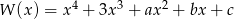 jest podzielny przez trójmian
jest podzielny przez trójmian 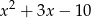 , a przy dzieleniu przez dwumian
, a przy dzieleniu przez dwumian 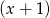 daje resztę -36. Wyznacz współczynniki
daje resztę -36. Wyznacz współczynniki 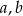 i
i  wielomianu.
wielomianu.
Oblicz granicę funkcji 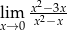 .
.
Oblicz granicę funkcji 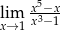 .
.
Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji 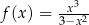 .
.
Wyznacz najmniejszą wartość funkcji 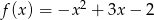 w przedziale
w przedziale 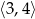 .
.
Oblicz największą wartość funkcji 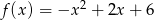 w przedziale
w przedziale 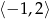 .
.
Oblicz najmniejszą wartość funkcji kwadratowej 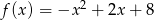 w przedziale
w przedziale 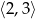 .
.
Wyznacz największą wartość funkcji 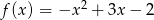 w przedziale
w przedziale 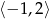 .
.
Oblicz najmniejszą wartość funkcji kwadratowej 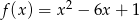 w przedziale
w przedziale 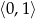 .
.
Wyznacz najmniejszą wartość funkcji 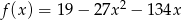 na przedziale
na przedziale 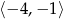 .
.
Oblicz największą wartość funkcji kwadratowej 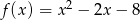 w przedziale
w przedziale 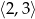 .
.
Wiedząc, że  jest miarą kąta ostrego i
jest miarą kąta ostrego i 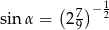 , wyznacz liczbę
, wyznacz liczbę  , dla której
, dla której 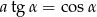 .
.
Maksymalny zbiór, na którym funkcja rzeczywista
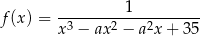
jest rosnąca jest jedyny i jest niepustym przedziałem postaci 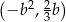 , dla pewnej liczby całkowitej
, dla pewnej liczby całkowitej 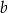 . Wyznacz dziedzinę funkcji
. Wyznacz dziedzinę funkcji 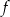 oraz jej największą wartość na przedziale
oraz jej największą wartość na przedziale ![[− 2,3]](https://img.zadania.info/zad/6362203/HzadT4x.gif) .
.
Liczby rzeczywiste  i
i  spełniają warunek
spełniają warunek 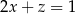 . Wyznacz takie wartości
. Wyznacz takie wartości  i
i  , dla których wyrażenie
, dla których wyrażenie 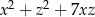 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
Liczby rzeczywiste 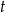 i
i 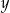 spełniają warunek
spełniają warunek 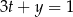 . Wyznacz takie wartości
. Wyznacz takie wartości 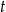 i
i 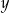 , dla których wyrażenie
, dla których wyrażenie 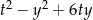 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
Korzystając z definicji funkcji rożnowartościowej wykaż, że funkcja 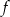 określona wzorem
określona wzorem 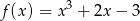 jest rożnowartościowa.
jest rożnowartościowa.

