Funkcja 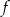 określona jest wzorem
określona jest wzorem
dla każdego  . Pochodna funkcji
. Pochodna funkcji  w punkcie
w punkcie 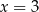 jest równa 0. Wyznacz zbiór wszystkich wartości, jakie funkcja przyjmuje na przedziale
jest równa 0. Wyznacz zbiór wszystkich wartości, jakie funkcja przyjmuje na przedziale ![[− 4,4]](https://img.zadania.info/zad/6437130/HzadT5x.gif) .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Funkcja  określona jest wzorem
określona jest wzorem
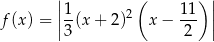
dla każdego 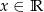 . Pochodna funkcji
. Pochodna funkcji 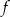 w punkcie
w punkcie 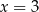 jest równa 0. Wyznacz zbiór wszystkich wartości, jakie funkcja przyjmuje na przedziale
jest równa 0. Wyznacz zbiór wszystkich wartości, jakie funkcja przyjmuje na przedziale ![[− 4,4]](https://img.zadania.info/zad/6437130/HzadT5x.gif) .
.
Liczba 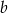 jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji
jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji 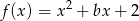 jest większa od
jest większa od 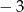 . Wyznacz liczbę
. Wyznacz liczbę 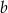 .
.
Funkcja kwadratowa określona wzorem 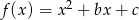 osiąga wartości ujemne wtedy i tylko wtedy, gdy
osiąga wartości ujemne wtedy i tylko wtedy, gdy 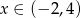 .
.
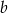 i
i  .
.  , wartości funkcji
, wartości funkcji 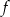 są mniejsze od wartości funkcji kwadratowej
są mniejsze od wartości funkcji kwadratowej 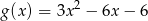 .
. 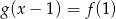 .
.Wykaż, że jeśli 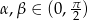 ,
, 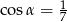 i
i 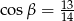 , to
, to 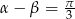 .
.
Wyznacz te wartości parametru 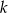 , dla których funkcja
, dla których funkcja 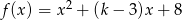 jest malejąca w przedziale
jest malejąca w przedziale 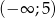 i rosnąca w przedziale
i rosnąca w przedziale 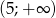 .
.
Oblicz wartość funkcji 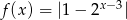 dla argumentu
dla argumentu
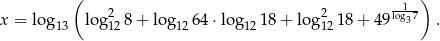
Oblicz wartość funkcji 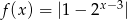 dla argumentu
dla argumentu 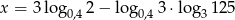 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 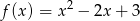 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 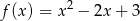 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 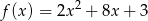 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 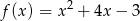 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 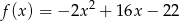 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 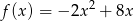 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci iloczynowej wzorem 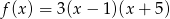 .
.
Funkcja 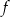 jest określona wzorem
jest określona wzorem 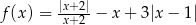 , dla każdej liczby rzeczywistej
, dla każdej liczby rzeczywistej 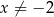 . Wyznacz zbiór wartości tej funkcji.
. Wyznacz zbiór wartości tej funkcji.
Wykaż, że
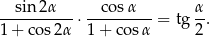
Wyznacz dziedzinę tej tożsamości.
Wykaż, że
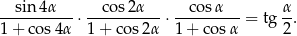
Wyznacz dziedzinę tej tożsamości.
Reszta z dzielenia wielomianu 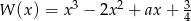 przez dwumian
przez dwumian 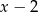 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
Reszta z dzielenia wielomianu 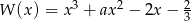 przez dwumian
przez dwumian 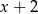 jest równa 1. Oblicz wartość współczynnika
jest równa 1. Oblicz wartość współczynnika  .
.
Oblicz granicę funkcji 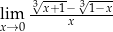 .
.
Wyznacz zbiór wartości funkcji 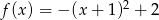 .
.
Wyznacz najmniejszą i największą wartość funkcji: 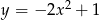 w przedziale
w przedziale 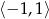 .
.
Wyznacz zbiór wartości funkcji 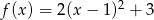 .
.
Wyznacz zbiór wartości funkcji 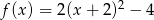 .
.
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę 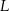 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
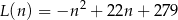
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 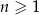 i
i 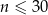 . Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia.
. Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia.
Oblicz granicę funkcji 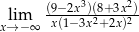 .
.
Wyznacz najmniejszą i największą wartość funkcji 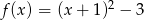 w przedziale
w przedziale 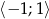 .
.
Liczby rzeczywiste  i
i  spełniają warunek
spełniają warunek 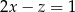 . Wyznacz takie wartości
. Wyznacz takie wartości  i
i  , dla których wyrażenie
, dla których wyrażenie 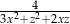 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
Wyznacz ekstrema lokalne funkcji 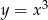 .
.
Wyznacz ekstrema lokalne funkcji 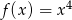 .
.
Wykaż, że 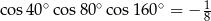 .
.
Dany jest wielomian 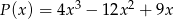 , gdzie
, gdzie 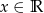 .
.
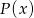 przyjmuje wartość równą 27?
przyjmuje wartość równą 27? 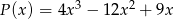 oraz
oraz 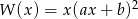 są równe. Wyznacz
są równe. Wyznacz  i
i 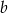 .
.Funkcja 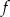 określona jest wzorem
określona jest wzorem 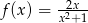 .
.
 jest nieparzysta.
jest nieparzysta.  zawiera się w zbiorze
zawiera się w zbiorze 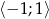 .
.