Prosta 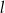 , na której leży punkt
, na której leży punkt 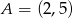 , przecina parabolę o równaniu
, przecina parabolę o równaniu 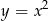 w dwóch różnych punktach
w dwóch różnych punktach 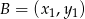 i
i 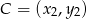 . Oblicz wartość współczynnika kierunkowego prostej
. Oblicz wartość współczynnika kierunkowego prostej 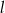 , przy której suma
, przy której suma 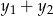 osiągnie wartość najmniejszą.
osiągnie wartość najmniejszą.
/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum/Najmniejsza suma
Dane są punkty 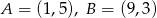 i prosta
i prosta 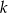 o równaniu
o równaniu 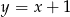 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 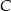 leżącego na prostej
leżącego na prostej 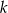 , dla którego suma
, dla którego suma 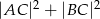 jest najmniejsza.
jest najmniejsza.
Na płaszczyźnie dane są punkty 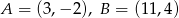 . Na prostej o równaniu
. Na prostej o równaniu 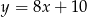 znajdź punkt
znajdź punkt 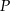 , dla którego suma
, dla którego suma 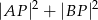 jest najmniejsza.
jest najmniejsza.
Wyznacz współrzędne punktu 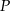 leżącego na prostej o równaniu
leżącego na prostej o równaniu 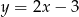 , którego suma kwadratów odległości od punktów
, którego suma kwadratów odległości od punktów 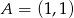 i
i 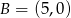 jest najmniejsza.
jest najmniejsza.
Na prostej 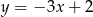 wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
Wyznacz współrzędne punktu 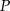 leżącego na wykresie funkcji
leżącego na wykresie funkcji 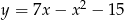 , dla którego suma odległości od osi układu współrzędnych jest najmniejsza.
, dla którego suma odległości od osi układu współrzędnych jest najmniejsza.
Dany jest trójkąt 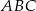 , w którym
, w którym 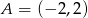 i
i 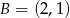 . Wierzchołek
. Wierzchołek 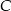 leży na prostej o równaniu
leży na prostej o równaniu 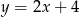 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 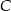 , dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
, dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
Dany jest trójkąt 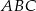 , w którym
, w którym 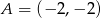 i
i 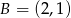 . Wierzchołek
. Wierzchołek 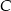 leży na prostej o równaniu
leży na prostej o równaniu 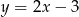 . Wyznacz współrzędne wierzchołka
. Wyznacz współrzędne wierzchołka 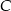 , dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
, dla którego suma kwadratów długości boków trójkąta jest najmniejsza.
Na prostej 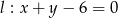 wyznacz taki punkt
wyznacz taki punkt 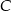 , aby długość łamanej
, aby długość łamanej 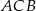 , gdzie
, gdzie 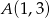 ,
, 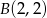 , była najmniejsza. Uzasadnij swoje rozumowanie.
, była najmniejsza. Uzasadnij swoje rozumowanie.
Wyznacz taki punkt 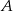 na prostej
na prostej 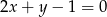 , by suma kwadratów jego odległości od osi układu była najmniejsza.
, by suma kwadratów jego odległości od osi układu była najmniejsza.
Dane są punkty 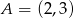 i
i 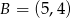 . Na prostej o równaniu
. Na prostej o równaniu 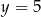 wyznacz punkt
wyznacz punkt 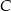 tak, aby łamana
tak, aby łamana 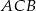 miała jak najmniejszą długość. Odpowiedź uzasadnij.
miała jak najmniejszą długość. Odpowiedź uzasadnij.

