Wspólne styczne dwóch okręgów stycznych zewnętrznie przecinają się pod kątem 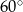 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność/Dwa okręgi styczne
Do dwóch stycznych zewnętrznie okręgów poprowadzono dwie wspólne styczne: jedną zewnętrzną i jedną wewnętrzną. Proste te przecinają się pod kątem 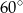 . Wyznacz stosunek długości promieni tych okręgów.
. Wyznacz stosunek długości promieni tych okręgów.
Dwa okręgi o promieniach 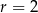 i
i 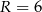 są styczne zewnętrznie i są styczne do wspólnej prostej
są styczne zewnętrznie i są styczne do wspólnej prostej 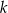 . Wykaż, że prosta
. Wykaż, że prosta 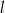 przechodząca przez środki
przechodząca przez środki 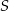 i
i 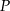 tych okręgów przecina prostą
tych okręgów przecina prostą 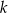 pod kątem
pod kątem  (zobacz rysunek).
(zobacz rysunek).
Suma pól dwóch kół stycznych zewnętrznie jest równa 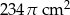 . Oblicz promienie tych kół, jeżeli wiadomo, że obwód większego koła jest o 400% większy od obwodu mniejszego koła.
. Oblicz promienie tych kół, jeżeli wiadomo, że obwód większego koła jest o 400% większy od obwodu mniejszego koła.
Dwa okręgi o promieniach  i
i 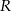 (
(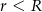 ) są styczne zewnętrznie. Prosta
) są styczne zewnętrznie. Prosta 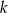 nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej
nie przechodzi przez punkt wspólny tych okręgów i jest styczna do każdego z nich. Znajdź promień okręgu stycznego zewnętrznie do danych okręgów i stycznego do prostej 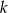 . Rozważ dwa przypadki.
. Rozważ dwa przypadki.
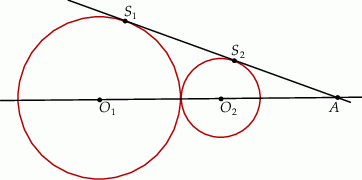
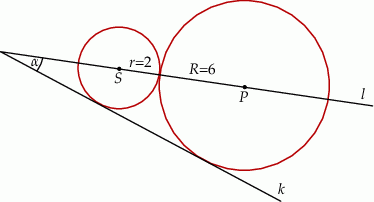
Zewnętrznie styczne okręgi o środkach 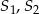 i promieniach
i promieniach 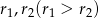 są styczne do prostej
są styczne do prostej 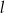 . Kąt między prostą przechodzącą przez środki okręgów i prostą
. Kąt między prostą przechodzącą przez środki okręgów i prostą 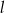 ma miarę
ma miarę 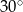 . Wyznacz długości promieni okręgów, jeśli wiadomo, że ich suma jest równa 24.
. Wyznacz długości promieni okręgów, jeśli wiadomo, że ich suma jest równa 24.
Dwa okręgi są styczne zewnętrznie, a odległość ich środków jest równa 19. Gdyby te okręgi były styczne wewnętrznie, to ta odległość wynosiłaby 5. Wyznacz długości promieni tych okręgów.
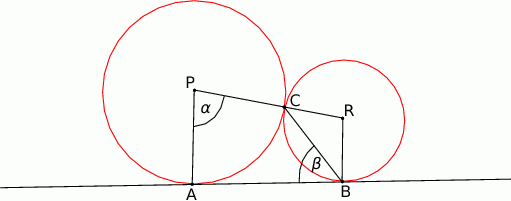
Dane są dwa okręgi o środkach w punktach 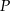 i
i 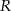 , styczne zewnętrznie w punkcie
, styczne zewnętrznie w punkcie 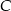 . Prosta
. Prosta 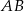 jest styczna do obu okręgów odpowiednio w punktach
jest styczna do obu okręgów odpowiednio w punktach 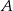 i
i 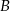 oraz
oraz 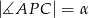 i
i  (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że  .
.
Dane są dwa okręgi o środkach w punktach 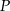 i
i 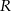 , styczne wewnętrznie w punkcie
, styczne wewnętrznie w punkcie 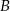 . Prosta
. Prosta 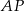 jest styczna do mniejszego okręgu w punkcie
jest styczna do mniejszego okręgu w punkcie 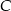 oraz
oraz 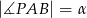 i
i 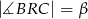 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 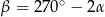 .
.
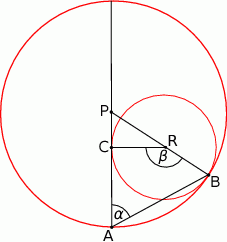
Dane są 2 koła styczne zewnętrznie o promieniach 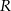 i
i  (
(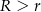 ) oraz środkach
) oraz środkach  i
i 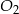 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach
. Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach 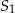 i
i 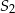 odpowiednio (
odpowiednio (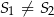 ). Oblicz pole trójkąta
). Oblicz pole trójkąta 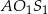 , gdzie
, gdzie 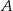 jest punktem przecięcia się prostych
jest punktem przecięcia się prostych 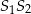 i
i 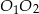 .
.