Wykres funkcji 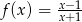 przekształcono w symetrii względem prostej
przekształcono w symetrii względem prostej 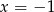 i otrzymano wykres funkcji
i otrzymano wykres funkcji 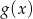 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 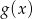 .
.
/Szkoła średnia/Funkcje - wykresy/Homografia
- Zaznacz w układzie współrzędnych zbiór
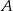 punktów, których współrzędne
punktów, których współrzędne 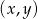 spełniają warunek:
spełniają warunek: 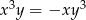 .
. - Wiedząc, że wykres funkcji homograficznej
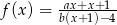 nie ma punktów wspólnych ze zbiorem
nie ma punktów wspólnych ze zbiorem 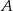 wyznacz
wyznacz  i
i 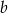 .
.
Na rysunku przedstawiono fragment wykresu funkcji 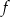 , który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem
, który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem 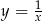 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 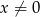 .
.
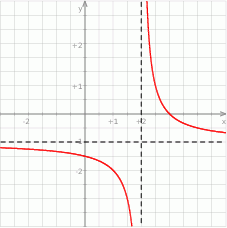
- Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji
 są większe od 0.
są większe od 0. - Podaj miejsce zerowe funkcji
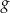 określonej wzorem
określonej wzorem 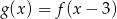 .
.
Na rysunku obok przedstawiony jest fragment wykresu funkcji 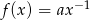 , gdzie
, gdzie 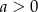 . Rozpatrzmy figury
. Rozpatrzmy figury 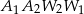 i
i 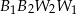 , gdzie
, gdzie 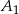 i
i 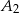 są dowolnymi różnymi punktami na dodatniej półosi osi
są dowolnymi różnymi punktami na dodatniej półosi osi 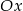 . Udowodnij, że figury te mają równe pola.
. Udowodnij, że figury te mają równe pola.
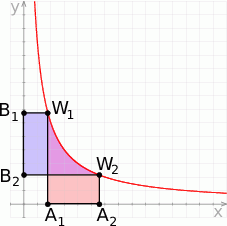
Wykres funkcji 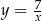 przesunięto o wektor
przesunięto o wektor ![→ v = [− 3,k]](https://img.zadania.info/zad/2263710/HzadT1x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 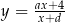 . Wyznacz
. Wyznacz 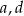 i
i 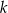 .
.
Wykres funkcji 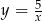 przesunięto o wektor
przesunięto o wektor ![→ v = [2,k]](https://img.zadania.info/zad/9133400/HzadT1x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 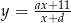 . Wyznacz
. Wyznacz 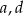 i
i 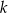 .
.
W oparciu o wykres funkcji określonej wzorem 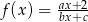 , wyznacz
, wyznacz 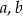 i
i  .
.
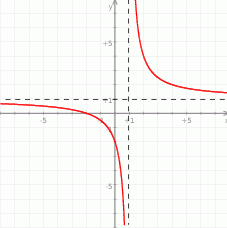
Wykres funkcji 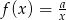 dla
dla 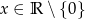 , gdzie
, gdzie 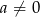 , przesunięto o wektor
, przesunięto o wektor ![→u = [− 3,2]](https://img.zadania.info/zad/2875082/HzadT3x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 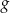 . Do wykresu funkcji
. Do wykresu funkcji 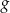 należy punkt
należy punkt 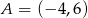 . Oblicz
. Oblicz  , następnie rozwiąż nierówność
, następnie rozwiąż nierówność 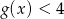 .
.
Dana jest funkcja 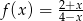 , gdzie
, gdzie 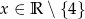 .
.
- Wyznacz wszystkie punkty należące do wykresu funkcji
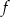 , których obie współrzędne są liczbami pierwszymi.
, których obie współrzędne są liczbami pierwszymi. - Podaj zbiór tych argumentów, dla których funkcja
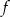 przyjmuje wartości nieujemne.
przyjmuje wartości nieujemne. - Naszkicuj wykres funkcji
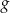 , jeśli
, jeśli 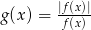 .
.
Funkcja 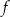 jest określona wzorem
jest określona wzorem 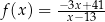 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 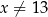 . Punktem kratowym nazywamy punkt w kartezjańskim układzie współrzędnych, którego obie współrzędne są liczbami całkowitymi. Wyznacz wszystkie punkty kratowe należące do wykresu funkcji
. Punktem kratowym nazywamy punkt w kartezjańskim układzie współrzędnych, którego obie współrzędne są liczbami całkowitymi. Wyznacz wszystkie punkty kratowe należące do wykresu funkcji 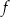 .
.
Wyznacz wszystkie wartości parametru 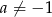 , dla których wykres funkcji
, dla których wykres funkcji 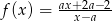 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 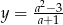 .
.
Wykres funkcji 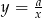 , gdzie
, gdzie 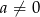 przesunięto o wektor
przesunięto o wektor ![[2,3]](https://img.zadania.info/zad/5074509/HzadT2x.gif) i otrzymano wykres funkcji, która ma dokładnie dwa punkty wspólne z okręgiem o równaniu
i otrzymano wykres funkcji, która ma dokładnie dwa punkty wspólne z okręgiem o równaniu 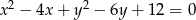 . Wyznacz
. Wyznacz  .
.
Dana jest funkcja 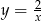 . Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor
. Napisz wzór funkcji otrzymanej po przesunięciu danej funkcji o wektor ![→u = [1,− 5]](https://img.zadania.info/zad/5948271/HzadT1x.gif) . Narysuj oba wykresy.
. Narysuj oba wykresy.
Dane są funkcje 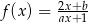 oraz
oraz 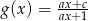 , o których wiadomo, że ich wykresy mają punkt wspólny
, o których wiadomo, że ich wykresy mają punkt wspólny 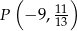 , a miejscem zerowym funkcji
, a miejscem zerowym funkcji 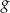 jest liczba:
jest liczba: 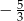 . Wyznacz wartości parametrów
. Wyznacz wartości parametrów 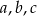 .
.
Rysunek przedstawia fragment wykresu funkcji 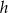 , określonej wzorem
, określonej wzorem 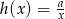 dla
dla 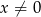 . Wiadomo, że do wykresu funkcji
. Wiadomo, że do wykresu funkcji 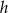 należy punkt
należy punkt  .
.
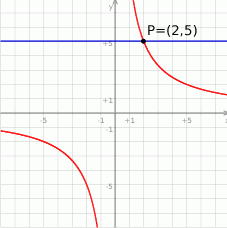
- Oblicz wartość współczynnika
 .
. - Ustal, czy liczba
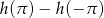 jest dodatnia czy ujemna.
jest dodatnia czy ujemna. - Rozwiąż nierówność
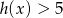 .
.
Dana jest funkcja 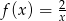 . Narysuj wykres i wyznacz przedziały monotoniczności funkcji
. Narysuj wykres i wyznacz przedziały monotoniczności funkcji 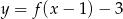 .
.
Wykres funkcji 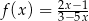 przesunięto o wektor
przesunięto o wektor ![[− 3,2]](https://img.zadania.info/zad/7906055/HzadT1x.gif) i otrzymano wykres funkcji
i otrzymano wykres funkcji 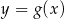 . Oblicz granicę
. Oblicz granicę
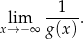
Sporządź wykres funkcji 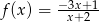 .
.
Punkt 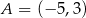 jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem
jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem 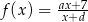 , gdy
, gdy 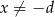 . Oblicz iloraz
. Oblicz iloraz 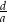 .
.
Punkt 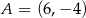 jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem
jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem 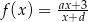 , gdy
, gdy 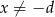 . Oblicz iloraz
. Oblicz iloraz 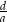 .
.
Rysunek przedstawia fragment wykresu funkcji określonej wzorem 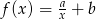 dla
dla 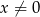 .
.
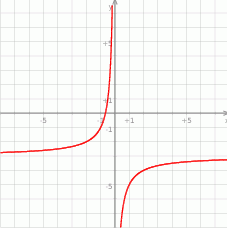
- Odczytaj z wykresu rozwiązanie nierówności
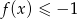 .
. - Oblicz współczynniki
 i
i 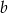 .
.
Na rysunku przedstawiony jest wykres funkcji 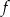 określonej wzorem
określonej wzorem 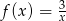 dla
dla 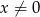 .
.
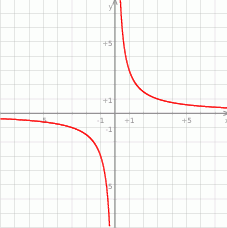
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi  . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 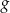 o wzorze
o wzorze 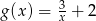 dla
dla 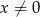 .
.
- Narysuj wykres funkcji
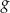 .
. - Oblicz największą wartość funkcji
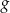 w przedziale
w przedziale 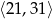 .
. - Podaj, o ile jednostek wzdłuż osi
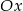 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 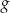 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.

