W graniastosłupie prawidłowym czworokątnym 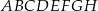 połączono punkty będące środkami krawędzi
połączono punkty będące środkami krawędzi 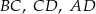 i
i 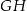 . Wyznacz objętość powstałej bryły wiedząc, że
. Wyznacz objętość powstałej bryły wiedząc, że 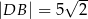 i kąt
i kąt 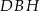 ma miarę
ma miarę 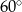 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W graniastosłupie prawidłowym czworokątnym 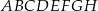 połączono punkty będące środkami krawędzi
połączono punkty będące środkami krawędzi 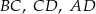 i
i 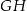 . Wyznacz objętość powstałej bryły wiedząc, że
. Wyznacz objętość powstałej bryły wiedząc, że 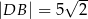 i kąt
i kąt 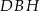 ma miarę
ma miarę 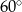 .
.

Wysokość prostopadłościanu o podstawie kwadratowej jest dwa razy dłuższa od krawędzi podstawy. Objętość prostopadłościanu jest równa 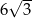 . Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
W graniastosłupie prawidłowym czworokątnym krawędź podstawy ma długość 5 cm, a krawędź boczna ma długość 4 cm. Przez wierzchołek górnej podstawy i przekątną dolnej poprowadzono płaszczyznę. Oblicz pole otrzymanego przekroju. Rozpatrz 2 przypadki.
Graniastosłup prawidłowy czworokątny o krawędzi 4 cm i wysokości 3 cm przecięto płaszczyzną, która zawiera przekątne przeciwległych ścian bocznych. Jakie pole ma ten przekrój?
Krawędź podstawy graniastosłupa prawidłowego czworokątnego ma długość 8 cm, a jego wysokość 12 cm. Połączono środki dwóch sąsiednich krawędzi dolnej podstawy oraz najbardziej odległy od tego odcinka wierzchołek górnej podstawy. Oblicz pole otrzymanego trójkąta.
Kąt między przekątnymi sąsiednich ścian bocznych prostopadłościanu o podstawie kwadratowej jest równy 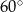 . Krawędź podstawy ma długość 12. Wyznacz pole powierzchni całkowitej tego prostopadłościanu i kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy prostopadłościanu.
. Krawędź podstawy ma długość 12. Wyznacz pole powierzchni całkowitej tego prostopadłościanu i kąt nachylenia przekątnej ściany bocznej do płaszczyzny podstawy prostopadłościanu.
Objętość graniastosłupa prawidłowego czworokątnego jest równa 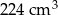 , a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do
, a promień okręgu opisanego na podstawie ma długość 4 cm. Wyznacz miarę kąta między przekątnymi sąsiednich ścian bocznych wychodzącymi z tego samego wierzchołka graniastosłupa. Wynik podaj z dokładnością do 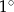 .
.
Objętość graniastosłupa prawidłowego czworokątnego jest równa 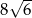 . Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
. Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 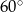 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.
