Kacper i Hela otrzymali identyczne zestawy 138 drewnianych klocków, w których każdy klocek jest sześcianem o krawędzi 2 cm. Kacper ze swoich klocków zbudował graniastosłup prawidłowy czworokątny i zostały mu dwa klocki, których nie było gdzie dołożyć. Hela ze swoich klocków zbudowała trzy identyczne graniastosłupy prawidłowe czworokątne i zostały jej trzy klocki, których nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej graniastosłupa zbudowanego przez Kacpra do pola powierzchni całkowitej jednego z graniastosłupów zbudowanych przez Helę. Wynik podaj w postaci ułamka nieskracalnego.

 .
.  .
.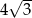 wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa. 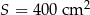 . Oblicz objętość i pole powierzchni całkowitej tej bryły .
. Oblicz objętość i pole powierzchni całkowitej tej bryły . 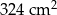 . Oblicz objętość tej bryły .
. Oblicz objętość tej bryły . 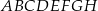 , którego podstawą jest prostokąt
, którego podstawą jest prostokąt 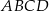 . W tym graniastosłupie
. W tym graniastosłupie 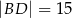 , a ponadto
, a ponadto 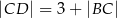 oraz
oraz 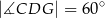 (zobacz rysunek).
(zobacz rysunek). 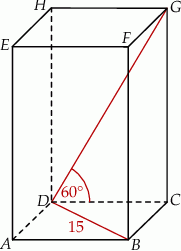
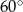 . Zaznacz na rysunku ten przekrój i oblicz jego pole.
. Zaznacz na rysunku ten przekrój i oblicz jego pole.  o podstawach
o podstawach  i
i 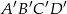 , oraz krawędziach bocznych
, oraz krawędziach bocznych 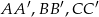 i
i 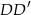 . Oblicz pole trójkąta
. Oblicz pole trójkąta 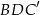 wiedząc, że przekątna ściany bocznej ma długość 13 i jest nachylona do podstawy pod takim kątem
wiedząc, że przekątna ściany bocznej ma długość 13 i jest nachylona do podstawy pod takim kątem  , że
, że 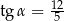 .
. 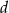 i tworzą kąt o mierze
i tworzą kąt o mierze  . Oblicz objętość tego graniastosłupa.
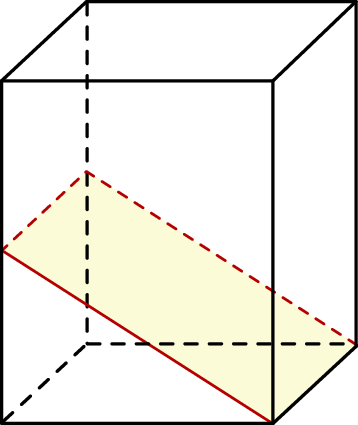
. Oblicz objętość tego graniastosłupa.  i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary
i wysokości dwa razy dłuższej od krawędzi podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary 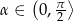 . Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
. Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.  i wysokości trzy razy dłuższej od podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary
i wysokości trzy razy dłuższej od podstawy, przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do podstawy pod kątem miary 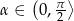 . Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki.
. Oblicz pole otrzymanego przekroju. Rozważ wszystkie możliwe przypadki. 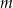 jest nachylona do płaszczyzny podstawy pod kątem
jest nachylona do płaszczyzny podstawy pod kątem  . Wiadomo, że
. Wiadomo, że 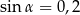 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.  , taki że
, taki że 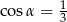 . Pole podstawy tego graniastosłupa wynosi
. Pole podstawy tego graniastosłupa wynosi 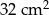 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.  , taki że
, taki że 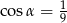 . Pole podstawy tego graniastosłupa wynosi
. Pole podstawy tego graniastosłupa wynosi 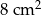 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.  takim, że
takim, że 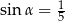 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.  takim, że
takim, że 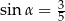 . Wyznacz objętość tego graniastosłupa.
. Wyznacz objętość tego graniastosłupa.  . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa.  . Oblicz pole powierzchni całkowitej tego graniastosłupa.
. Oblicz pole powierzchni całkowitej tego graniastosłupa. 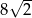 i jest nachylona do płaszczyzny podstawy pod kątem
i jest nachylona do płaszczyzny podstawy pod kątem 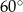 . Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek.
. Oblicz objętość i pole powierzchni całkowitej prostopadłościanu i wykonaj rysunek. 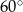 . Jedna z krawędzi podstawy ma długość 8. Wyznacz objętość i pole powierzchni całkowitej tego prostopadłościanu.
. Jedna z krawędzi podstawy ma długość 8. Wyznacz objętość i pole powierzchni całkowitej tego prostopadłościanu.  . Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem
. Przekątna tego graniastosłupa jest nachylona do płaszczyzny jego podstawy pod kątem  (zobacz rysunek).
(zobacz rysunek). 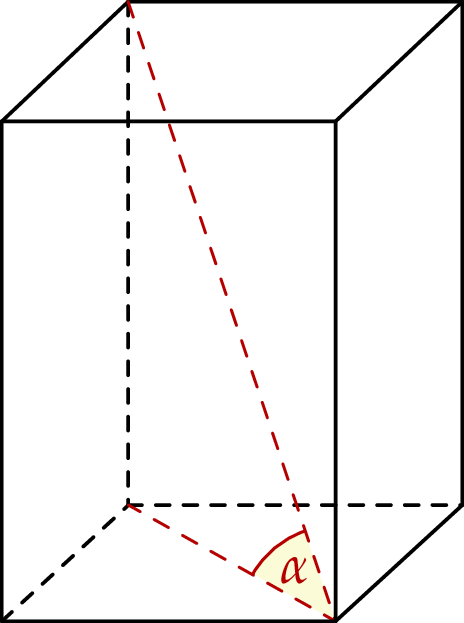
 oraz pole powierzchni całkowitej tego graniastosłupa.
oraz pole powierzchni całkowitej tego graniastosłupa. 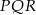
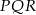 .
. 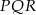 .
.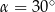 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa. 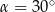 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.  . Wyznacz
. Wyznacz 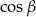 , gdzie
, gdzie 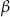 jest kątem nachylenia płaszczyzny przekroju do płaszczyzny podstawy bryły.
jest kątem nachylenia płaszczyzny przekroju do płaszczyzny podstawy bryły. 