Suma cyfr pewnej liczby dwucyfrowej wynosi 12. Jeżeli od liczby utworzonej z przestawienia cyfr liczby początkowej odejemiemy 8 to otrzymamy liczbę 3 razy mniejszą od liczby początkowej. Znajdz tę liczbę.
/Konkursy/Zadania/Liczby
Grzyby w lesie zawierają 90% wody w swojej masie, a po wysuszeniu zawierają 15% wody w swojej masie . Oblicz ile trzeba zebrać grzybów aby uzyskać 0,5 kg suszonych grzybów.
Wykaż, że jeśli  jest liczbą nieparzystą, to liczba
jest liczbą nieparzystą, to liczba 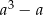 jest podzielna przez 12.
jest podzielna przez 12.
Wykaż, że dla każdej liczby naturalnej 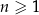 liczba
liczba 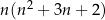 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 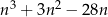 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej 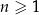 liczba
liczba 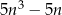 jest podzielna przez 30.
jest podzielna przez 30.
Uzasadnij, że dla każdej liczby całkowitej 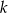 liczba
liczba 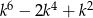 jest podzielna przez 36.
jest podzielna przez 36.
Wykaż, że jeżeli 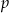 jest liczbą pierwszą większą od 3 to
jest liczbą pierwszą większą od 3 to 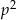 przy dzieleniu przez 24 daje resztę 1.
przy dzieleniu przez 24 daje resztę 1.
Wykaż, że liczba  jest dla dowolnej liczby naturalnej
jest dla dowolnej liczby naturalnej  kwadratem liczby całkowitej.
kwadratem liczby całkowitej.
Która z liczb jest większa 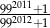 , czy
, czy 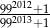 ?
?
Która z liczb jest większa: 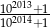 , czy
, czy 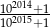 ?
?
Wyznacz wszystkie liczby naturalne  , dla których
, dla których 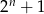 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Pewnego dnia postawiłem dla psów miskę z psimi ciasteczkami. Najpierw przyszedł najstarszy pies i zjadł połowę ciasteczek, i jeszcze jedno. Potem przyszedł drugi pies zjadł połowę tego, co znalazł i jeszcze jedno ciasteczko. Potem przyszedł trzeci pies i także zjadł połowę tego, co znalazł i jeszcze jedno ciasteczko. Wreszcie przyszedł czwarty najmniejszy piesek i zjadł połowę tego, co zostało, i jeszcze jedno ciasteczko, wtedy ciasteczka się skończyły. Ile ich było na początku w misce?
Udowodnij, że dla dowolnych kątów 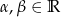 prawdziwe są tożsamości
prawdziwe są tożsamości
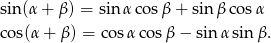
Wykaż, że jeżeli 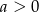 i
i 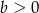 oraz
oraz 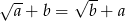 to
to 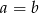 lub
lub 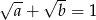 .
.
Wykaż, że jeżeli liczby dodatnie  i
i 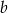 spełniają warunek
spełniają warunek
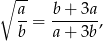
to 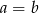 .
.
Zosia, Marysia i Ania weszły do klasy gdzie na wielkim transparencie były zapisane liczby od 1 do 7777. Zosia zakreśliła na różowo wszystkie liczby podzielne przez 3. Marysia zakreśliła na zielono wszystkie liczby podzielne przez 4. Ania zakreśliła na fioletowo wszystkie liczby podzielne przez 6. Ile liczb zostało zakreślonych dwukrotnie (bez względu na kolor)?
W kryptogramie różnym literom odpowiadają różne cyfry. Podaj rozwiązanie.
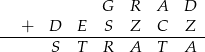
Dla jakich  należących do zbioru liczb naturalnych liczba
należących do zbioru liczb naturalnych liczba 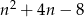 jest kwadratem liczby naturalnej?
jest kwadratem liczby naturalnej?
Rozwiąż nierówność 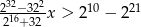 . Podaj najmniejszą liczbę całkowitą spełniającą tę nierówność.
. Podaj najmniejszą liczbę całkowitą spełniającą tę nierówność.
Znajdź wszystkie liczby naturalne  takie, że liczba
takie, że liczba 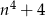 jest liczbą pierwszą.
jest liczbą pierwszą.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 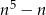 jest podzielna przez 30.
jest podzielna przez 30.
Wyznacz najmniejszą liczbę 4-cyfrową, która przy dzieleniu przez 7 daje resztę 6, a przy dzieleniu przez 6 daje resztę 5.
Wykaż, że jeśli 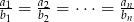 i
i 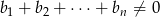 , to
, to 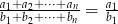 .
.
Wykaż, że 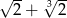 jest liczbą niewymierną.
jest liczbą niewymierną.

