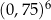Liczba 16 razy większa od 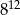 jest równa
jest równa
A) 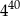 B)
B) 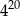 C)
C) 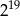 D)
D) 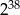
/Szkoła podstawowa
Liczba 81 razy mniejsza od 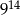 jest równa
jest równa
A) 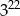 B)
B) 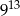 C)
C) 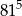 D)
D) 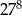
Na boku 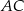 trójkąt równobocznego
trójkąt równobocznego 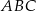 o polu równym
o polu równym 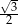 zbudowano równoramienny trójkąt prostokątny
zbudowano równoramienny trójkąt prostokątny 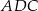 .
.
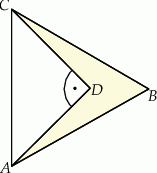
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole czworokąta 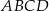 jest równe jest równe 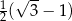 . . | P | F |
Obwód czworokąta 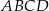 jest równy jest równy 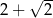 . . | P | F |
Pole równoległoboku przedstawionego na rysunku jest równe
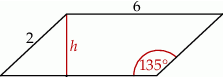
A) 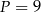 B)
B) 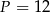 C)
C) 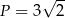 D)
D) 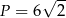
Na rysunku przedstawiono trzy figury: kwadrat 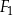 , kwadrat
, kwadrat 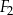 i prostokąt
i prostokąt 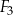 , oraz podano ich wymiary.
, oraz podano ich wymiary.

Czy z figur 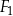 ,
, 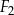 ,
, 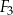 można ułożyć, bez rozcinania tych figur, kwadrat
można ułożyć, bez rozcinania tych figur, kwadrat 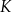 o polu
o polu 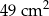 ? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | suma obwodów figur 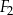 i i 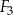 jest równa obwodowi kwadratu jest równa obwodowi kwadratu 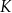 . . |
| B) | suma pól figur 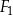 , , 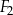 i i 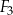 jest równa jest równa 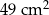 . . |
| C) | suma długości dowolnych boków figur 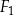 , , 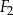 i i 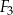 nie jest równa 7 cm. nie jest równa 7 cm. |
Na rysunku przedstawiono trzy figury: kwadrat 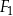 , prostokąt
, prostokąt 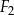 i prostokąt
i prostokąt 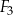 , oraz podano ich wymiary.
, oraz podano ich wymiary.

Czy z figur 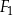 ,
, 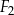 ,
, 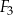 można ułożyć, bez rozcinania tych figur, kwadrat
można ułożyć, bez rozcinania tych figur, kwadrat 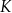 o obwodzie 28 cm? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
o obwodzie 28 cm? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | suma obwodów figur 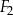 i i 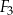 jest równa obwodowi kwadratu jest równa obwodowi kwadratu 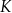 . . |
| B) | suma pól figur 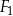 , , 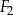 i i 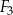 nie jest równa nie jest równa 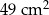 . . |
| C) | suma długości dowolnych boków figur 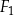 , , 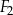 i i 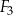 nie jest równa 7 cm. nie jest równa 7 cm. |
Na rysunku przedstawiono prostopadłościenny klocek o wymiarach 8 cm, 7 cm i 3 cm oraz sposób, w jaki rozcięto go na cztery części: sześcian (I) i trzy prostopadłościany (II, III, IV).
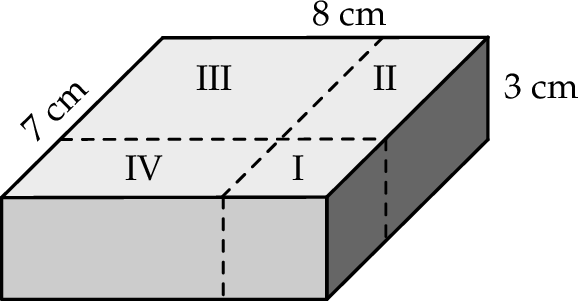
Objętość prostopadłościanu II jest równa
A) 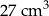 B)
B) 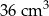 C)
C) 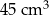 D)
D) 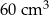
W stadninie koni pani Lucyny znajduje się 120 koni w czterech różnych umaszczeniach. Na diagramie przedstawiono w procentach udział poszczególnych umaszczeń, ale nie narysowano słupka z umaszczeniem karym.
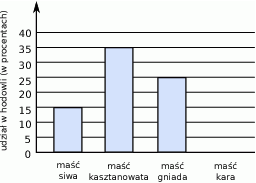
Ile jest koni gniadych w hodowli pani Lucyny?
A) 15 B) 20 C) 25 D) 30
W stadninie koni pani Lucyny znajduje się 120 koni w czterech różnych umaszczeniach. Na diagramie przedstawiono w procentach udział poszczególnych umaszczeń, ale nie narysowano słupka z umaszczeniem karym.
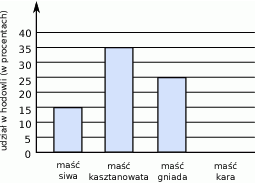
Jaki procent hodowli pani Lucyny stanowią konie kare?
A) 15% B) 20% C) 25% D) 30%
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
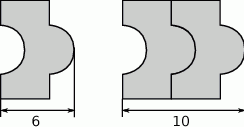
Ułożono wzór z 5 płytek, jak na rysunku.
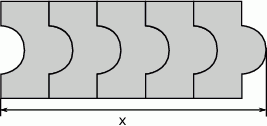
Odcinek
 ma długość
ma długośćA) 20 cm B) 22 cm C) 26 cm D) 30 cm
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
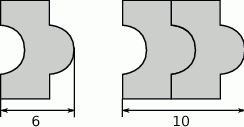
Ułożono wzór z 5 płytek, jak na rysunku.
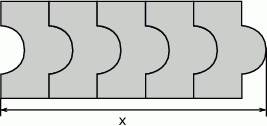
Które wyrażenie algebraiczne opisuje długość analogicznego do
 odcinka dla wzoru złożonego z
odcinka dla wzoru złożonego z  płytek?
płytek? A)
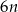 B)
B) 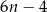 C)
C) 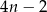 D)
D) 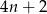
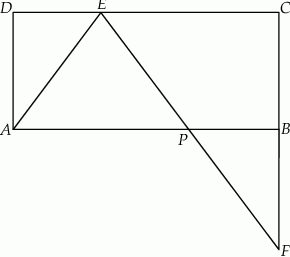
Dany jest prostokąt 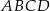 . Na boku
. Na boku 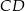 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 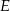 , że
, że 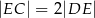 , a na boku
, a na boku 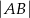 wybrano taki punkt
wybrano taki punkt 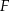 , że
, że 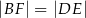 . Niech
. Niech 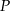 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 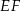 z prostą
z prostą 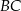 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty  i
i  są przystające.
są przystające.
Dany jest prostokąt 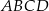 . Na boku
. Na boku 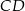 tego prostokąta wybrano taki punkt
tego prostokąta wybrano taki punkt 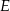 , że
, że 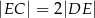 , a na przedłużeniu boku
, a na przedłużeniu boku 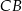 wybrano taki punkt
wybrano taki punkt 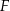 , że
, że 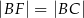 . Niech
. Niech 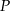 oznacza punkt przecięcia prostej
oznacza punkt przecięcia prostej 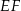 z prostą
z prostą 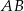 (zobacz rysunek). Wykaż, że trójkąty
(zobacz rysunek). Wykaż, że trójkąty 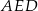 i
i 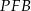 są przystające.
są przystające.
Trzy metalowe sześciany stopiono i z całości otrzymanego metalu odlano nowy sześcian, którego krawędź ma długość 60 cm. Dwa ze stopionych sześcianów miały krawędzie długości 30 cm i 50 cm. Jaka była długość krawędzi trzeciego ze stopionych sześcianów?
W tabeli podano, w jaki sposób zmienia się cena biletu na 1 przejazd metrem w zależności od pory dnia.
| Cena podstawowa biletu | 8 zł |
| Cena biletu w godzinach 16–18 | cena podstawowa podwyższona o 14% |
| Cena biletu w godzinach 7–8 | cena podstawowa podwyższona o 52% |
| Cena biletu w godzinach 22–24 | cena podstawowa obniżona o 36% |
| Cena biletu w pozostałych godzinach | cena podstawowa |
A) 4 zł B) 7,04 zł C) 1,12 zł D) 4,16 zł
W tabeli podano, w jaki sposób zmienia się cena biletu na 1 przejazd metrem w zależności od pory dnia.
| Cena podstawowa biletu | 8 zł |
| Cena biletu w godzinach 16–18 | cena podstawowa podwyższona o 14% |
| Cena biletu w godzinach 7–8 | cena podstawowa podwyższona o 52% |
| Cena biletu w godzinach 22–24 | cena podstawowa obniżona o 36% |
| Cena biletu w pozostałych godzinach | cena podstawowa |
| Cena biletu o godz. 22 jest o 50% niższa niż cena biletu o godz. 17 | P | F |
| Cena biletu o godz. 16 jest o 25% niższa niż cena biletu o godz. 7 | P | F |
Dany jest prostopadłościan o wymiarach 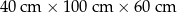 . Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
. Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
W 6 litrach napoju wiśniowego jest 2,4 litra czystego soku. Oblicz stężenie napoju, czyli zawartość procentową czystego soku w napoju wiśniowym.
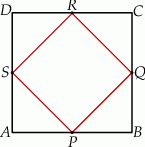
W kwadracie  połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat  .
.
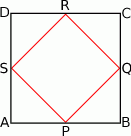
Kwadrat  jest podobny do kwadratu
jest podobny do kwadratu  w skali
w skali
A) 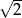 B) 2 C)
B) 2 C) 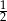 D)
D) 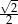
W kwadracie 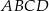 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat  .
.
Kwadrat  jest podobny do kwadratu
jest podobny do kwadratu  w skali
w skali
A) 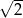 B) 2 C)
B) 2 C) 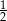 D)
D) 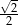
W dwóch litrowych butelkach była woda. Na wykresie przedstawiono, jak zmieniała się objętość wody w pierwszej butelce w trakcie przelewania do niej całej zawartości drugiej butelki.
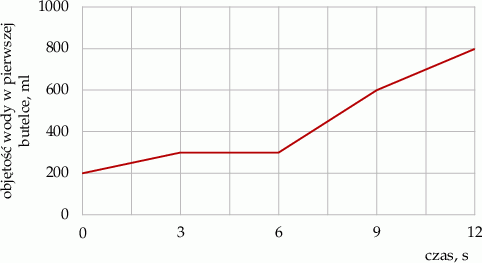
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na początku w pierwszej butelce było 200 ml wody, a w drugiej butelce było 800 ml wody. | P | F |
| W czasie ostatnich trzech sekund przelano 200 ml wody. | P | F |
Dane są liczby
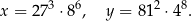
Iloczyn 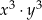 jest równy A/B.
jest równy A/B.
A) 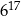 B)
B) 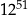
Iloraz 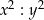 jest równy C/D.
jest równy C/D.
C) 144 D) 12
Oblicz 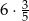 .
.
Oblicz 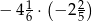 .
.
Oblicz 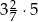 .
.
Oblicz 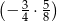 .
.
Oblicz 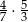 .
.
Oblicz 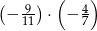 .
.
Oblicz 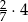 .
.
Agata na dużej kartce w kratkę narysowała figurę złożoną z 40 połączonych odcinków, które kolejno ponumerowała liczbami naturalnymi od 1 do 40. Wszystkie komórki kratki są takimi samymi kwadratami. Na rysunku przedstawiono fragment tej figury, złożony z ośmiu początkowych odcinków. Kolejne odcinki tej figury Agata narysowała według tej samej reguły, którą zastosowała do narysowania odcinków 1–8.
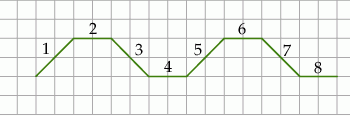
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Proste zawierające odcinki o numerach 1 oraz 7 są wzajemnie prostopadłe. | P | F |
| Proste zawierające odcinki o numerach 5 oraz 33 są wzajemnie równoległe. | P | F |
Agata na dużej kartce w kratkę narysowała figurę złożoną z 40 połączonych odcinków, które kolejno ponumerowała liczbami naturalnymi od 1 do 40. Wszystkie komórki kratki są takimi samymi kwadratami. Na rysunku przedstawiono fragment tej figury, złożony z ośmiu początkowych odcinków. Kolejne odcinki tej figury Agata narysowała według tej samej reguły, którą zastosowała do narysowania odcinków 1–8.
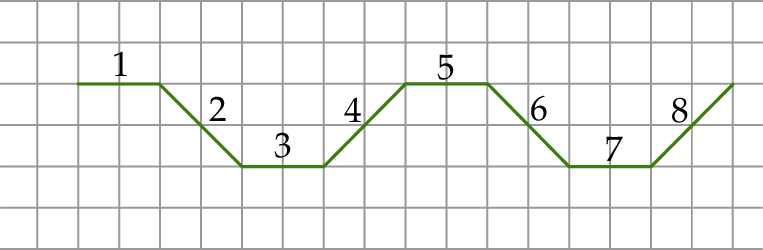
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Proste zawierające odcinki o numerach 2 oraz 8 są wzajemnie prostopadłe. | P | F |
| Proste zawierające odcinki o numerach 5 oraz 32 są wzajemnie równoległe. | P | F |
Punkt 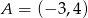 jest początkiem odcinka
jest początkiem odcinka  , gdzie
, gdzie 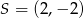 jest jego środkiem. Punkt
jest jego środkiem. Punkt 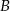 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 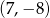 B)
B) 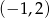 C)
C) 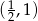 D)
D) 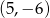
Punkt 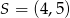 jest środkiem odcinka
jest środkiem odcinka 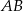 , w którym
, w którym 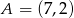 . Punkt
. Punkt 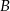 ma współrzędne:
ma współrzędne:
A) 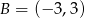 B)
B) 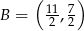 C)
C) 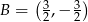 D)
D) 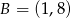
Punkt 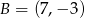 jest końcem odcinka
jest końcem odcinka 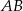 , gdzie
, gdzie 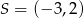 jest jego środkiem. Punkt
jest jego środkiem. Punkt 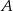 , który jest początkiem tego odcinka ma współrzędne
, który jest początkiem tego odcinka ma współrzędne
A) 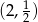 B)
B) 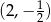 C)
C) 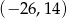 D)
D) 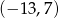
Punkt 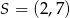 jest środkiem odcinka
jest środkiem odcinka 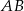 , w którym
, w którym 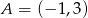 . Punkt
. Punkt 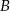 ma współrzędne:
ma współrzędne:
A) 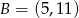 B)
B) 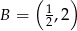 C)
C) 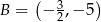 D)
D) 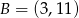
Punkt 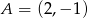 jest początkiem odcinka
jest początkiem odcinka 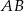 , gdzie
, gdzie 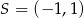 jest jego środkiem. Punkt
jest jego środkiem. Punkt 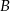 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 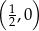 B)
B) 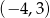 C)
C) 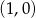 D)
D) 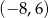
W układzie współrzędnych punkt 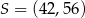 jest środkiem odcinka
jest środkiem odcinka 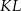 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 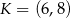 . Zatem
. Zatem
A) 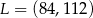 B)
B) 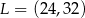 C)
C) 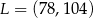 D)
D) 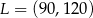
Punkt 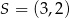 jest środkiem odcinka
jest środkiem odcinka 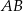 , w którym
, w którym 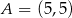 . Punkt
. Punkt 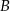 ma współrzędne
ma współrzędne
A) 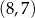 B)
B)  C)
C) 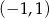 D)
D) 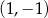
Punkt 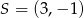 jest środkiem odcinka
jest środkiem odcinka 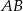 i
i 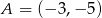 . Punkt
. Punkt 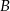 ma współrzędne
ma współrzędne
A) 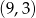 B)
B) 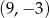 C)
C) 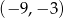 D)
D) 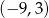
Punkt 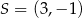 jest środkiem odcinka
jest środkiem odcinka 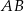 , w którym
, w którym 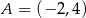 . Punkt
. Punkt 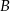 ma współrzędne
ma współrzędne
A) 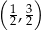 B)
B) 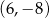 C)
C) 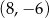 D)
D) 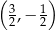
W układzie współrzędnych zaznaczono dwa punkty: 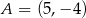 i
i 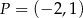 . Punkt
. Punkt 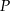 jest środkiem odcinka
jest środkiem odcinka 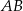 . Jakie współrzędne ma punkt B?
. Jakie współrzędne ma punkt B?
A) 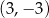 B)
B) 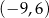 C)
C) 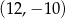 D)
D) 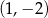
W układzie współrzędnych punkt 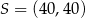 jest środkiem odcinka
jest środkiem odcinka 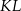 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 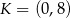 . Zatem
. Zatem
A) 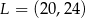 B)
B) 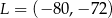 C)
C) 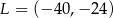 D)
D) 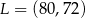
Punkt 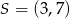 jest środkiem odcinka
jest środkiem odcinka 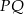 , gdzie
, gdzie 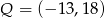 . Zatem punkt
. Zatem punkt 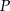 ma współrzędne
ma współrzędne
A) 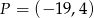 B)
B) 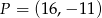 C)
C) 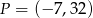 D)
D) 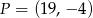
Punkt 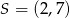 jest środkiem odcinka
jest środkiem odcinka 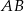 , w którym
, w którym 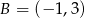 . Punkt
. Punkt 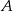 ma współrzędne:
ma współrzędne:
A) 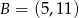 B)
B) 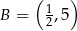 C)
C) 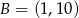 D)
D) 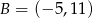
Dane są punkty 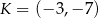 oraz
oraz 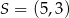 . Punkt
. Punkt 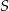 jest środkiem odcinka
jest środkiem odcinka 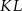 . Wtedy punkt
. Wtedy punkt 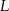 ma współrzędne
ma współrzędne
A) 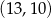 B)
B) 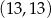 C)
C) 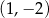 D)
D) 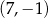
W układzie współrzędnych zaznaczono dwa punkty: 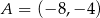 i
i 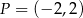 . Punkt
. Punkt 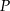 jest środkiem odcinka
jest środkiem odcinka 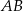 . Jakie współrzędne ma punkt
. Jakie współrzędne ma punkt 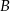 ?
?
A) 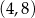 B)
B) 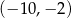 C)
C) 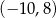 D)
D) 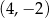
Punkt 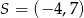 jest środkiem odcinka
jest środkiem odcinka 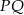 , gdzie
, gdzie 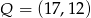 . Zatem punkt
. Zatem punkt 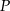 ma współrzędne
ma współrzędne
A) 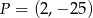 B)
B) 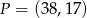 C)
C) 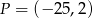 D)
D) 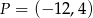
Punkt 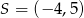 jest środkiem odcinka
jest środkiem odcinka 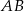 i
i 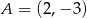 . Punkt
. Punkt 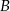 ma współrzędne
ma współrzędne
A) 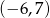 B)
B) 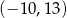 C)
C) 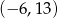 D)
D) 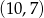
Deska dębowa ma 3 m długości, 25 cm szerokości i 3 cm grubości. 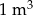 drewna dębowego waży 660 kg. Ile kilogramów waży ta deska?
drewna dębowego waży 660 kg. Ile kilogramów waży ta deska?
Iloraz 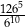 jest równy A/B.
jest równy A/B.
A) 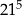 B)
B) 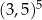
Iloczyn 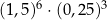 jest równy C/D.
jest równy C/D.
C) 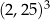 D)
D)