Oblicz pole trójkąta przedstawionego na rysunku.
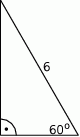
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz pole trójkąta przedstawionego na rysunku.

Oblicz pole trójkąta przedstawionego na rysunku.
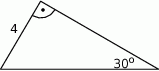
Do udziału w podchodach zgłosiło się 54 chłopców i 24 dziewczynki. Uczestników postanowiono podzielić na zespoły w ten sposób, aby we wszystkich zespołach była ta sama liczba dziewcząt i ta sama liczba chłopców.
Ile maksymalnie zespołów utworzono?
A) 9 B) 2 C) 3 D) 6
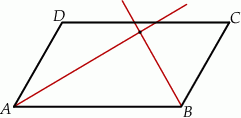
Uzasadnij, że dwusieczne dwóch sąsiednich kątów równoległoboku przecinają się pod kątem prostym.
Uzasadnij, że dwusieczne kątów 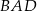 i
i 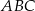 równoległoboku
równoległoboku 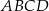 są prostopadłe.
są prostopadłe.
Odcinek 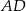 jest wysokością przedstawionego na rysunku trójkąta równoramiennego
jest wysokością przedstawionego na rysunku trójkąta równoramiennego 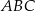 , w którym
, w którym 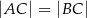 . Udowodnij, że
. Udowodnij, że 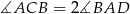 .
.
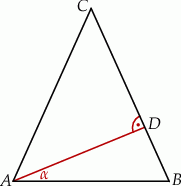
Wykaż, że miara kąta między wysokością trójkąta równoramiennego poprowadzoną do ramienia a podstawą tego trójkąta jest dwa razy mniejsza od miary kąta zawartego między ramionami tego trójkąta.
Z trójkąta 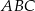 o obwodzie 50 wycięto kwadrat
o obwodzie 50 wycięto kwadrat 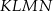 o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
o obwodzie 20 (tak jak na rysunku). Obwód zacieniowanej figury jest równy
A) 64 B) 60 C) 75 D) 70
W sześciokąt foremny 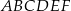 wpisano trójkąt równoboczny tak jak przedstawiono na rysunku.
wpisano trójkąt równoboczny tak jak przedstawiono na rysunku.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trójkąta 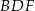 jest większy niż 80% obwodu sześciokąta jest większy niż 80% obwodu sześciokąta 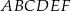 . . | P | F |
Pole trójkąta 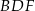 jest 3 razy większe od pola trójkąta jest 3 razy większe od pola trójkąta 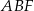 . . | P | F |
Rozszyfruj podaną datę i zapisz ją cyframi arabskimi: MCCCLXXXVI.
Rozszyfruj podaną datę i zapisz ją cyframi arabskimi: MCDXXXIV.
Rozszyfruj podaną datę i zapisz ją cyframi arabskimi: MCCCLXXVII.
Rozszyfruj podaną datę i zapisz ją cyframi arabskimi: MCCCLI.
Trener chce zamówić 25 nowych piłek do tenisa. Piłki wybranej firmy sprzedawane są w opakowaniach po 3 sztuki albo po 4 sztuki. Ile opakowań każdego rodzaju powinien zamówić trener, aby mieć dokładnie 25 nowych piłek? Podaj wszystkie możliwości.
Grupa 29 osób chce się podzielić na kilka grup pięcio i trzyosobowych. Ile grup trzyosobowych może powstać w ten sposób? Podaj wszystkie możliwości.
Równanie 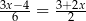
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Równanie 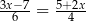
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Równanie 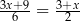
A) nie ma rozwiązań B) ma dokładnie jedno rozwiązanie
C) ma dokładnie dwa rozwiązania D) ma nieskończenie wiele rozwiązań
Automat biletowy drukuje 30 biletów w ciągu 2 minut i 6 sekund. Który wzór opisuje zależność między liczbą wydrukowanych biletów ( ), a czasem ich druku w sekundach (
), a czasem ich druku w sekundach (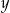 ), jeżeli tempo drukowania biletów nie ulega zmianie?
), jeżeli tempo drukowania biletów nie ulega zmianie?
A) 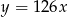 B)
B) 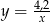 C)
C) 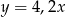 D)
D) 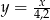
Jeżeli odcinek 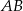 podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części (
podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części ( ), na którą dzielimy odcinek
), na którą dzielimy odcinek 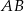 , a długością (
, a długością (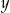 ) jednej takiej części w milimetrach?
) jednej takiej części w milimetrach?
A) 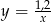 B)
B) 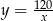 C)
C) 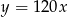 D)
D) 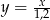
Na rysunku poniżej przedstawiono siatkę pewnej bryły. Punkty: 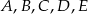 są środkami jej krawędzi.
są środkami jej krawędzi.
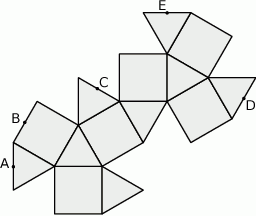
Po złożeniu bryły z tej siatki punkt 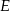 pokryje się z punktem
pokryje się z punktem
A) 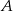 B)
B) 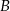 C)
C) 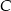 D)
D) 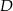
Wyrażenie 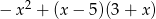 można przekształcić do postaci
można przekształcić do postaci
A) 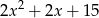 B)
B) 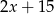 C)
C) 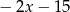 D)
D) 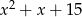
Wyrażenie 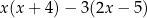 można przekształcić równoważnie do postaci
można przekształcić równoważnie do postaci
A) 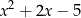 B)
B) 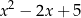 C)
C) 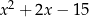 D)
D) 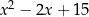
Wyrażenie 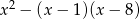 można przekształcić do postaci
można przekształcić do postaci
A) 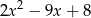 B)
B) 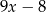 C)
C) 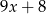 D)
D) 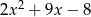
Wyrażenie 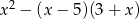 można przekształcić do postaci
można przekształcić do postaci
A) 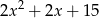 B)
B) 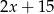 C)
C) 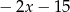 D)
D) 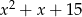
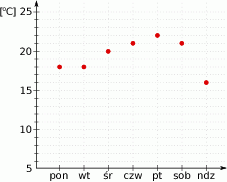
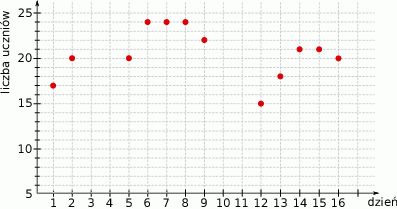
Na wykresie obok przedstawiono temperatury zanotowane w kolejnych dniach.
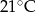 ?
? Wykres przedstawia obecność uczniów klasy liczącej 24 osoby na początku marca.
W trapezie prostokątnym kąt ostry ma miarę 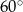 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 6 B) 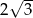 C)
C) 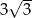 D)
D) 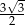
W trapezie prostokątnym kąt ostry ma miarę 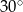 , a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
, a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
A) 4 B) 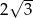 C)
C) 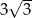 D)
D) 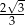
W trapezie prostokątnym kąt ostry ma miarę 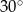 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 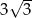 B)
B) 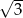 C) 6 D)
C) 6 D) 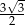
W trapezie prostokątnym kąt ostry ma miarę 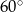 , a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
, a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
A) 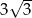 B) 4 C)
B) 4 C) 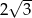 D)
D) 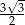
Cenę pewnego towaru obniżono najpierw o 30%, a potem o 50%. Początkowa cena została więc ostatecznie obniżona o 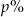 . Wynika stąd, że
. Wynika stąd, że
A) 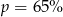 B)
B) 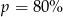 C)
C) 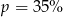 D)
D) 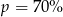
Cenę towaru obniżano dwa razy. Pierwsza obniżka wynosiła 10%, a druga 20%. O ile procent w wyniku obu obniżek spadła cena towaru?
A) o 24% B) o 26% C) o 28% D) o 30%
Cenę książki obniżano dwukrotnie, najpierw o 10%, a po miesiącu jeszcze o 5%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 14% B) 14,5% C) 15% D) 15,5%
Cenę pewnego towaru podwyższono najpierw o 20%, a potem jeszcze o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 30% C) 32% D) 34%
Cena towaru została podwyższona o 30%, a po pewnym czasie nową, wyższą cenę ponownie podwyższono, tym razem o 10%. W rezultacie obu podwyżek wyjściowa cena towaru zwiększyła się o
A) 15% B) 20% C) 40% D) 43%
Cenę pewnego towaru podwyższono o 20%, a następnie nową cenę tego towaru podwyższono o 30%. Takie dwie podwyżki ceny tego towaru można zastąpić równoważną im jedną podwyżką
A) o 50% B) o 56% C) o 60% D) o 66%
Cenę pewnego towaru obniżono najpierw o 20%, a potem o 30%. Początkowa cena została więc ostatecznie obniżona o 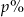 . Wynika stąd, że
. Wynika stąd, że
A) 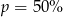 B)
B) 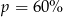 C)
C) 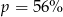 D)
D) 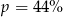
Cenę biurka obniżono o 10%, a następnie nową cenę obniżono o 30%. W wyniku obu tych zmian cena biurka zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 43% B) 40% C) 37% D) 63%
Cenę nart obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 30%. W wyniku obniżek cena nart zmniejszyła się o
A) 44% B) 50% C) 56% D) 60%
Cenę drukarki obniżono o 20%, a następnie nową cenę obniżono o 10%. W wyniku obu tych zmian cena drukarki zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 18% B) 28% C) 30% D) 72%
Cenę komputera obniżano dwukrotnie, najpierw o 20%, a po miesiącu jeszcze o 10%. W wyniku obu obniżek cena komputera zmniejszyła się o
A) 31% B) 30% C) 29% D) 28%
Cenę pewnego towaru obniżano dwukrotnie, za każdym razem o 20%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 40% B) o 36% C) o 32% D) o 28%
Cenę pewnego towaru obniżono o 20%, a następnie nową cenę tego towaru obniżono o 30%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 50% B) o 56% C) o 44% D) o 66%
Cenę książki obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 10%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 25% B) 28% C) 29% D) 30%
Cenę pewnego towaru podwyższono najpierw o 10%, a potem jeszcze o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 21% C) 22% D) 10%
Cenę pewnego towaru obniżono najpierw o 40%, a potem o 70%. Początkowa cena została więc ostatecznie obniżona o 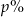 . Wynika stąd, że
. Wynika stąd, że
A) 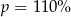 B)
B) 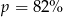 C)
C) 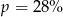 D)
D) 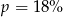
Na kuli ziemskiej występuje 450 000 gatunków roślin, ale zdołano zbadać własności tylko 20% z nich. Stwierdzono, że 30% zbadanych roślin ma własności lecznicze. W Polsce występuje 1,2% z tych gatunków roślin.
W ilu gatunkach występujących na kuli ziemskiej stwierdzono własności lecznicze?
A) 90 000 B) 27 000 C) 2 700 D) 9 000
Na kuli ziemskiej występuje 450 000 gatunków roślin, ale zdołano zbadać własności tylko 20% z nich. Stwierdzono, że 30% zbadanych roślin ma własności lecznicze. W Polsce występuje 1,2% z tych gatunków roślin.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Własności lecznicze stwierdzono w ponad 10% wszystkich gatunków roślin. | P | F |
| W Polsce występuje ponad 400 gatunków roślin leczniczych. | P | F |
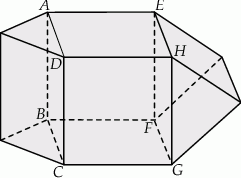
Na rysunkach przedstawiono tę samą bryłę widzianą z dwóch stron. Każda ze ścian tej bryły jest albo kwadratem, albo trójkątem równobocznym. Kwadratem jest też czworokąt  (patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.
(patrz rysunki). Każda krawędź ma długość 2. Jaką objętość ma ta bryła? Zapisz obliczenia.
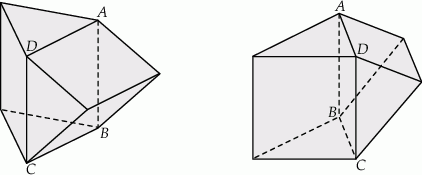
Na rysunku przedstawiono bryłę, której każda ściana jest albo kwadratem, albo trójkątem równobocznym. Kwadratami są też czworokąty  i
i  . Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
. Każda krawędź ma długość 4. Jaką objętość ma ta bryła? Zapisz obliczenia.
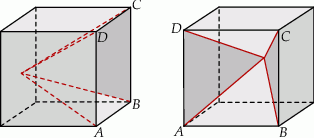
Z drewnianego sześcianu o krawędzi długości 6 cm wycięto ostrosłup prawidłowy czworokątny o wysokości równej krawędzi sześcianu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Jaką objętość ma ta bryła? Zapisz obliczenia.
Stożek o wysokości 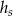 i walec o wysokości
i walec o wysokości 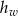 mają takie same podstawy o polu
mają takie same podstawy o polu 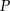 . Stożek ma dwa razy większą objętość niż walec, czyli
. Stożek ma dwa razy większą objętość niż walec, czyli 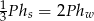 .
.
Zależność między wysokością stożka a wysokością walca można zapisać za pomocą równości
A) 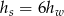 B)
B) 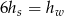 C)
C) 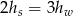 D)
D) 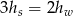
Po usunięciu jednej liczby z listy danych: 3, 2, 4, 1, 5, 1, 4, 1, 5, 2 średnia arytmetyczna zwiększyła się o 0,2. Którą liczbę usunięto z listy?
A) 1 B) 2 C) 3 D) 4
Po usunięciu jednej liczby z listy danych: 3, 2, 5, 4, 1, 5, 2, 4, 1, 5 średnia arytmetyczna zmniejszyła się o 0,2. Którą liczbę usunięto z listy?
A) 2 B) 3 C) 4 D) 5
W trójkącie równobocznym bok jest o 6 cm dłuższy od wysokości trójkąta. Oblicz pole i obwód tego trójkąta.
W trójkącie równobocznym wysokość jest o 3 cm krótsza od boku trójkąta. Oblicz pole i obwód tego trójkąta.
