Na półkuli o promieniu 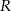 opisano stożek w ten sposób, że środek podstawy stożka pokrywa się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?
opisano stożek w ten sposób, że środek podstawy stożka pokrywa się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?
/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema
Spodek wysokości ostrosłupa 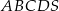 pokrywa się ze środkiem rombu
pokrywa się ze środkiem rombu 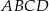 w jego podstawie oraz
w jego podstawie oraz 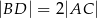 ,
, 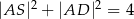 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 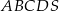 jeżeli wiadomo, że pole trójkąta
jeżeli wiadomo, że pole trójkąta 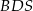 jest największe możliwe.
jest największe możliwe.
Tekturowy karton ma mieć kształt prostopadłościanu, którego podstawa jest prostokątem o jednym z boków dłuższym od drugiego o 24 cm. Suma wszystkich krawędzi tego prostopadłościanu ma być równa 480 cm.
-
Napisz wzór funkcji
 wyrażającej całkowite pole zewnętrznej powierzchni kartonu, w zależności od długości
wyrażającej całkowite pole zewnętrznej powierzchni kartonu, w zależności od długości  krótszej krawędzi jego podstawy. Podaj dziedzinę funkcji
krótszej krawędzi jego podstawy. Podaj dziedzinę funkcji 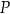 .
. -
Oblicz jakie powinny być wymiary tego kartonu tak, aby łączne pole powierzchni jego ścian było największe możliwe.
Suma długości wysokości i długości jednej krawędzi podstawy graniastosłupa prawidłowego czworokątnego jest równa 2. Jaką najmniejszą długość może mieć przekątna takiego graniastosłupa.
Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości  . Wymiary szkieletu zaznaczono na rysunku.
. Wymiary szkieletu zaznaczono na rysunku.
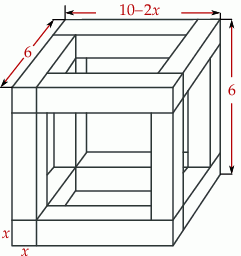
- Wyznacz objętość
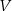 drewna potrzebnego do budowy szkieletu jako funkcję zmiennej
drewna potrzebnego do budowy szkieletu jako funkcję zmiennej  .
. - Wyznacz dziedzinę funkcji
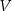 .
. - Oblicz tę wartość
 , dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja
, dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja 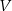 osiąga wartość największą. Oblicz tę największą objętość.
osiąga wartość największą. Oblicz tę największą objętość.
Rozpatrujemy wszystkie możliwe drewniane szkielety o kształcie przedstawionym na rysunku, wykonane z listewek. Każda z tych listewek ma kształt prostopadłościanu o podstawie kwadratu o boku długości  . Wymiary szkieletu zaznaczono na rysunku.
. Wymiary szkieletu zaznaczono na rysunku.
- Wyznacz objętość
 drewna potrzebnego do budowy szkieletu jako funkcję zmiennej
drewna potrzebnego do budowy szkieletu jako funkcję zmiennej  .
. - Wyznacz dziedzinę funkcji
 .
. - Oblicz tę wartość
 , dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja
, dla której zbudowany szkielet jest możliwie najcięższy, czyli kiedy funkcja 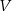 osiąga wartość największą. Oblicz tę największą objętość.
osiąga wartość największą. Oblicz tę największą objętość.
W ostrosłup prawidłowy czworokątny o wysokości 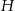 wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.
wpisano sześcian tak, że cztery jego wierzchołki należą do krawędzi bocznych ostrosłupa, a cztery pozostałe należą do płaszczyzny jego podstawy. Oblicz dla jakiej długości krawędzi podstawy ostrosłupa stosunek objętości ostrosłupa do objętości sześcianu jest najmniejszy możliwy.
Podstawą ostrosłupa jest trójkąt prostokątny, w którym tangens jednego z kątów ostrych jest równy 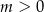 . Wszystkie krawędzie boczne ostrosłupa mają długość
. Wszystkie krawędzie boczne ostrosłupa mają długość 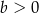 . Jakie powinno być pole podstawy ostrosłupa, aby jego objętość była największa? Oblicz tę największą objętość.
. Jakie powinno być pole podstawy ostrosłupa, aby jego objętość była największa? Oblicz tę największą objętość.
Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe 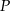 . Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
. Oblicz wysokość i promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe 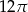 . Wyznacz wysokość tego spośród rozpatrywanych walców, którego objętość jest największa. Oblicz tę objętość.
. Wyznacz wysokość tego spośród rozpatrywanych walców, którego objętość jest największa. Oblicz tę objętość.
Rozpatrujemy wszystkie walce, których pole powierzchni całkowitej jest równe 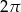 . Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.
. Oblicz promień podstawy tego walca, który ma największą objętość. Podaj tę największą objętość.
Rozważamy wszystkie graniastosłupy prawidłowe trójkątne o objętości 3456, których krawędź podstawy ma długość nie większą niż 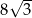 .
.
-
Wykaż, że pole
 powierzchni całkowitej graniastosłupa w zależności od długości
powierzchni całkowitej graniastosłupa w zależności od długości  krawędzi podstawy graniastosłupa jest określone wzorem
krawędzi podstawy graniastosłupa jest określone wzorem 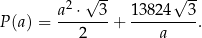
-
Wyznacz długość krawędzi podstawy tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
Z papierowego koła o promieniu 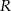 wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego
wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego  wyciętego wycinka? Wynik podaj w radianach.
wyciętego wycinka? Wynik podaj w radianach.
Rozpatrujemy wszystkie stożki, których pole powierzchni całkowitej jest równe 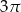 . Oblicz promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
. Oblicz promień podstawy tego stożka, który ma największą objętość. Podaj tę największą objętość.
W kulę o promieniu długości 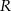 wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.
W kulę o promieniu długości 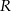 wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
W stożek o promieniu  i wysokości
i wysokości 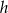 wpisujemy graniastosłupy sześciokątne prawidłowe tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Podaj wymiary graniastosłupa o największym polu powierzchni bocznej.
wpisujemy graniastosłupy sześciokątne prawidłowe tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Podaj wymiary graniastosłupa o największym polu powierzchni bocznej.
Podstawą ostrosłupa 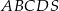 jest prostokąt o obwodzie 6. Krawędź
jest prostokąt o obwodzie 6. Krawędź 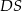 jest wysokością ostrosłupa i jest 3 razy dłuższa od krawędzi
jest wysokością ostrosłupa i jest 3 razy dłuższa od krawędzi 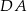 . Jakie największe pole może mieć przekrój ostrosłupa płaszczyzną wyznaczoną przez wierzchołki
. Jakie największe pole może mieć przekrój ostrosłupa płaszczyzną wyznaczoną przez wierzchołki 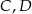 i środek krawędzi
i środek krawędzi 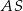 ?
?
Spośród tych graniastosłupów prawidłowych trójkątnych, których suma długości wszystkich krawędzi jest równa 18, wybierz graniastosłup o największej objętości. Oblicz tę maksymalną objętość.
Suma długości wszystkich krawędzi graniastosłupa prawidłowego sześciokątnego jest równa 36. Jakie są wymiary graniastosłupa o największej objętości?
Puszka konserwy ma kształt walca. Jaką wysokość i jaki promień podstawy powinna mieć ta puszka, aby przy objętości puszki 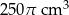 zużyć jak najmniej materiału na jej wykonanie.
zużyć jak najmniej materiału na jej wykonanie.
Dany jest zbiór wszystkich graniastosłupów prawidłowych sześciokątnych, których suma długości wszystkich krawędzi jest równa 216. Oblicz długość krawędzi podstawy i wysokość tego z danych graniastosłupów, który ma największe pole powierzchni bocznej.
Dany jest graniastosłup prawidłowy czworokątny, którego suma długości wszystkich krawędzi wynosi 12.
- Napisz wzór funkcji
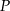 wyrażającej pole powierzchni całkowitej graniastosłupa, w zależności od długości krawędzi podstawy
wyrażającej pole powierzchni całkowitej graniastosłupa, w zależności od długości krawędzi podstawy  . Podaj dziedzinę funkcji
. Podaj dziedzinę funkcji 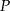 .
. - Wyznacz długości krawędzi graniastosłupa, dla których pole powierzchni całkowitej jest największe.

