Zadania na ekstrema/Stereometria - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema

Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramionach długości . Pole podstawy jest równe sumie pól dwóch przystających ścian bocznych graniastosłupa. Jakie powinny być długości pozostałych krawędzi graniastosłupa, aby jego objętość była największa?

Podstawą prostopadłościanu jest prostokąt o stosunku boków 1:3. Objętość bryły jest równa 12. Oblicz wymiary tego prostopadłościanu, aby jego powierzchnia całkowita była najmniejsza. Oblicz tę najmniejszą powierzchnię.

Suma długości krawędzi graniastosłupa prawidłowego czworokątnego jest równa 16. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?

Ukryj Podobne zadania

Suma krawędzi graniastosłupa prawidłowego trójkątnego jest równa 3. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?

Rozpatrujemy wszystkie ostrosłupy prawidłowe czworokątne o krawędzi bocznej równej 3. Oblicz pole powierzchni całkowitej tego z tych ostrosłupów, dla którego pole przekroju płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy oraz wierzchołek ostrosłupa jest największe możliwe.

Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma wysokości 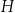ostrosłupa oraz promienia 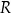okręgu opisanego na podstawie tego ostrosłupa jest równa 6.

Wykaż, że objętość 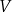każdego z takich ostrosłupów w zależności od długości 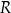promienia okręgu opisanego na podstawie ostrosłupa jest określona wzorem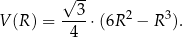

$√ -- --3- 2 3 V (R ) = 4 ⋅(6R − R ).$
Wyznacz długość promienia okręgu opisanego na podstawie tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tę największą objętość.

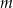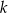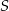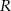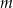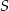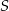Częścią wspólną płaszczyzny i kuli o środku i promieniu jest koło . Jaka musi być odległość płaszczyzny od środka kuli , aby stożek o podstawie i wierzchołku miał największą możliwą objętość? Oblicz tę maksymalną objętość.

Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

Ukryj Podobne zadania

Przekrojem osiowym stożka jest trójkąt o obwodzie 40. Podaj promień podstawy i wysokość stożka o największej objętości. Oblicz jego objętość.

Rozpatrujemy wszystkie stożki, w których suma długości tworzącej i promienia podstawy jest równa 2. Wyznacz wysokość tego spośród rozpatrywanych stożków, którego objętość jest największa. Oblicz tę objętość.

Rozważamy wszystkie walce o objętości 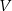. Wyznacz wysokość i promień podstawy tego z rozważanych walców, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to pole.

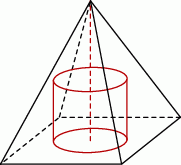
W metalowym ostrosłupie prawidłowym czworokątnym o wysokości 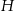i krawędzi podstawy wydrążono otwór w kształcie walca, którego oś symetrii pokrywa się z osią symetrii ostrosłupa (patrz rysunek). Otwór wydrążono przez podstawę ostrosłupa w ten sposób, że górna podstawa walca nie wystaje poza powierzchnię ostrosłupa. Jaka może być najmniejsza możliwa objętość otrzymanej w ten sposób bryły?

Rozpatrujemy wszystkie takie prostopadłościany, w których suma długości wszystkich krawędzi jest równa 80, pole powierzchni całkowitej jest równe 256 i długości wszystkich krawędzi są nie mniejsze niż 4. Objętość 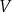każdego z rozpatrywanych prostopadłościanów można wyrazić za pomocą funkcji

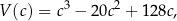
V(c) = c3 − 20c 2 + 12 8c,

gdzie [ ] c ∈ 4, 238 jest długością jednej z krawędzi bryły. Oblicz objętość tego spośród rozpatrywanych prostopadłościanów, którego objętość jest najmniejsza.

Trójkąt równoramienny o obwodzie 12 obraca się wokół swojej osi symetrii. Oblicz dla jakich długości boków trójkąta otrzymamy stożek, w którym różnica między polem powierzchni bocznej, a polem podstawy jest największa. Oblicz objętość tego stożka.

Rozpatrujemy wszystkie trójkąty równoramienne o ramionach długości 6. Oblicz cosinus kąta między ramionami tego z tych trójkątów, dla którego objętość bryły powstałej w wyniku obrotu trójkąta dokoła prostej zawierającej jego podstawę jest największa możliwa. Oblicz tę największą objętość.

Rozpatrujemy wszystkie walce o danym polu powierzchni całkowitej 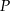. Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz tę największą objętość.

Ukryj Podobne zadania

Rozpatrujemy wszystkie graniastosłupy prawidłowe czworokątne o polu powierzchni całkowitej 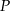. Wyznacz wysokość i długość krawędzi podstawy tego graniastosłupa, którego objętość jest największa. Oblicz tę największą objętość.

Romb o boku długości obraca się dokoła jednej z przekątnych. Wyznacz pole tego spośród takich rombów, dla którego objętość otrzymanej bryły jest największa.

W trójkąt prostokątny o przyprostokątnych o długościach 2 i 4 wpisano prostokąt w ten sposób, że dwa jego boki leżą na przyprostokątnych trójkąta, a jeden z wierzchołków prostokąta leży na przeciwprostokątnej trójkąta. Prostokąt ten obraca się dookoła prostej, zawierającej dłuższą przyprostokątną trójkąta, tworząc walec. Oblicz, który z walców, otrzymanych w powyższy sposób, posiada największe pole powierzchni bocznej i oblicz jego objętość.

Dany jest prostokątny arkusz kartonu o długości 80 cm i szerokości 50 cm. W czterech rogach tego arkusza wycięto kwadratowe naroża (zobacz rysunek).

ZINFO-FIGURE

Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długość boku wyciętych kwadratowych naroży, dla której objętość otrzymanego pudełka jest największa. Oblicz tę objętość.

Ukryj Podobne zadania

Dany jest prostokątny arkusz kartonu o długości 64 cm i szerokości 40 cm. Po dwóch stronach tego arkusza wycięto prostokąty, w których stosunek boków jest równy 1:2 (zacieniowane prostokąty na rysunku).

Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długości boków wyciętych prostokątów, dla których objętość otrzymanego pudełka jest największa. Oblicz tę objętość.

Wśród wszystkich graniastosłupów prawidłowych sześciokątnych, w których suma długości wszystkich krawędzi jest równa 24, jest taki, który ma największe pole powierzchni bocznej. Oblicz długość krawędzi podstawy tego graniastosłupa.

W ostrosłup prawidłowy czworokątny wpisujemy graniastosłupy prawidłowe czworokątne w ten sposób, że dolna podstawa graniastosłupa zawiera się podstawie ostrosłupa, a każdy z wierzchołków górnej podstawy należy do jednej z krawędzi bocznych ostrosłupa. Wiedząc, że każda z krawędzi ostrosłupa ma długość 6, oblicz jaka jest maksymalna możliwa powierzchnia boczna graniastosłupa.

Podstawą prostopadłościanu jest prostokąt, w którym jeden bok jest dwa razy dłuższy od drugiego. Pole powierzchni całkowitej tego prostopadłościanu jest równe 1. Jakie powinny być wymiary tego prostopadłościanu, aby jego objętość była największa? Oblicz tę największą objętość.

Ukryj Podobne zadania

Rozpatrujemy wszystkie graniastosłupy prawidłowe czworokątne, których pole powierzchni całkowitej jest równe 2. Oblicz długości krawędzi tego graniastosłupa, który ma największą objętość. Podaj tę największą objętość.

Zakład produkcyjny planuje wytwarzanie pojemników o objętości 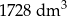3 1728 dm , które mają kształt otwartego graniastosłupa prawidłowego czworokątnego (bez górnej podstawy – zobacz rysunek).

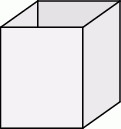
Koszt produkcji 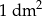2 1 dm podstawy tego pojemnika wynosi 0,3 zł, a koszt produkcji 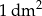1 dm 2 jego ścian bocznych wynosi 0,2 zł. Ponadto, do kosztu produkcji należy doliczyć niezbędne wzmocnienie krawędzi podstawy w cenie 4,2 zł za 1 dm długości. Oblicz jakie powinny być wymiary tego pojemnika tak, aby koszt jego produkcji był najmniejszy możliwy.

Strona 1 z 3