Jaką największą objętość ma walec wpisany w kulę o średnicy długości 12 cm?
/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema
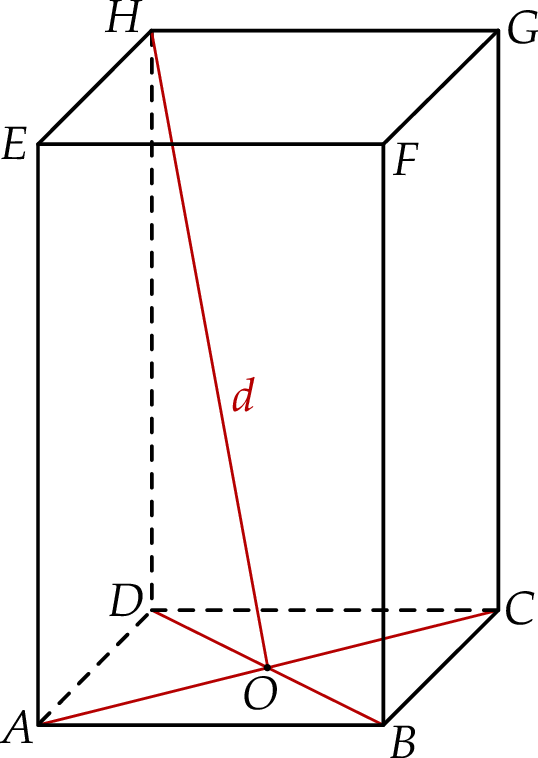
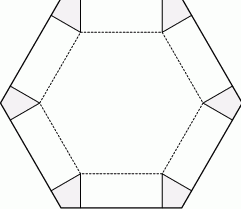
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne 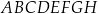 , w których odcinek łączący punkt
, w których odcinek łączący punkt 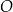 przecięcia przekątnych
przecięcia przekątnych 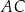 i
i 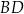 podstawy
podstawy 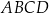 z dowolnym wierzchołkiem podstawy
z dowolnym wierzchołkiem podstawy 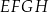 ma długość
ma długość 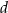 (zobacz rysunek).
(zobacz rysunek).
-
Wyznacz zależność objętości
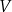 graniastosłupa od jego wysokości
graniastosłupa od jego wysokości 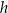 i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 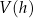 .
. -
Wyznacz wysokość tego z rozważanych graniastosłupów, którego objętość jest największa.
Rozważamy wszystkie graniastosłupy prawidłowe czworokątne 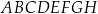 , w których odcinek łączący punkt
, w których odcinek łączący punkt 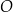 przecięcia przekątnych
przecięcia przekątnych 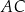 i
i 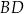 podstawy
podstawy 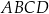 z dowolnym wierzchołkiem podstawy
z dowolnym wierzchołkiem podstawy 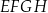 ma długość 3 (zobacz rysunek).
ma długość 3 (zobacz rysunek).
Wyznacz wymiary tego z rozważanych graniastosłupów, którego objętość jest największa. Oblicz tę największą objętość.
Firma logistyczna planuje produkcję pojemników w kształcie graniastosłupa prostego o objętości 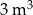 i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za
i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za 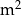 , a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za
, a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za 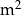 . Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.
. Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.
Rozpatrujemy wszystkie prostopadłościany o objętości 8, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:2 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 28. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.
Rozpatrujemy wszystkie prostopadłościany o objętości 27, których stosunek długości dwóch krawędzi wychodzących z tego samego wierzchołka jest równy 1:3 oraz suma długości wszystkich dwunastu krawędzi jest mniejsza od 52. Wyznacz pole powierzchni całkowitej prostopadłościanu jako funkcję długości jednej z jego krawędzi. Wyznacz dziedzinę tej funkcji. Oblicz wymiary tego spośród rozpatrywanych prostopadłościanów, którego pole powierzchni całkowitej jest najmniejsze.
Objętość graniastosłupa prawidłowego czworokątnego jest równa 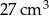 , Pole powierzchni całkowitej graniastosłupa jest funkcją długości jego krawędzi podstawy. Napisz wzór tej funkcji i wyznacz jej przedziały monotoniczności.
, Pole powierzchni całkowitej graniastosłupa jest funkcją długości jego krawędzi podstawy. Napisz wzór tej funkcji i wyznacz jej przedziały monotoniczności.
Rozpatrujemy wszystkie walce, których przekrojem osiowym jest prostokąt, w którym suma długości przekątnej i jednego boku jest równa 10. Oblicz wysokość i promień podstawy tego walca, którego objętość jest największa. Oblicz objętość tego walca.
Rozważamy wszystkie ostrosłupy prawidłowe trójkątne, w których suma długości wszystkich krawędzi jest równa 6.
-
Wyznacz zależność objętości
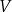 ostrosłupa od jego krawędzi podstawy
ostrosłupa od jego krawędzi podstawy  i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 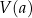 .
. -
Wyznacz długość krawędzi podstawy tego z rozważanych ostrosłupów, którego objętość jest największa. Oblicz tą największą objętość.
Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności 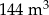 . Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
. Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– 100 zł za 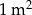 dna
dna
– 75 zł za 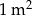 ściany bocznej.
ściany bocznej.
Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.
Zakład produkcyjny dostał zlecenie produkcji prostopadłościennych pudełek (całkowicie otwartych od góry) o objętości 60,75 litra. Dno pudełka ma być kwadratem i żaden z jego wymiarów nie może przekraczać 67,5 cm. Na koszt wykonania pudełka składają się – koszt wykonania 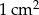 dna w wysokości 48 gorszy oraz koszt wykonania
dna w wysokości 48 gorszy oraz koszt wykonania 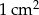 ściany bocznej w wysokości 36 groszy. Oblicz wymiary pudełka, dla których koszt jego produkcji będzie najmniejszy.
ściany bocznej w wysokości 36 groszy. Oblicz wymiary pudełka, dla których koszt jego produkcji będzie najmniejszy.
W stożek o promieniu podstawy 6 i wysokości 8 wpisujemy graniastosłupy prawidłowe sześciokątne tak, że jedna podstawa jest zawarta w podstawie stożka, a pozostałe wierzchołki należą do powierzchni bocznej stożka. Oblicz objętość graniastosłupa o największym polu powierzchni bocznej.
Rozważmy wszystkie graniastosłupy prawidłowe trójkątne o objętości 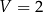 . Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
. Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
Rozważmy wszystkie graniastosłupy prawidłowe czworokątne o objętości 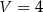 . Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
. Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
Mówimy, że walec jest wpisany w graniastosłup, jeżeli podstawy walca są zawarte w podstawach graniastosłupa, a powierzchnia boczna walca jest styczna do każdej ze ścian bocznych graniastosłupa (zobacz rysunek).
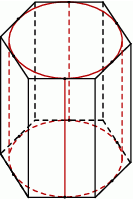
Rozpatrujemy wszystkie graniastosłupy prawidłowe sześciokątne takie, że suma długości promienia i wysokości walca wpisanego w ten graniastosłup jest równa 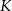 . Oblicz pole powierzchni całkowitej tego z rozważanych graniastosłupów, którego objętość jest największa.
. Oblicz pole powierzchni całkowitej tego z rozważanych graniastosłupów, którego objętość jest największa.
Z kartonu w kształcie trójkąta równobocznego o boku długości 120 cm odcięto trzy identyczne czworokąty w narożnikach (zobacz rysunek).
Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób pudełko w kształcie graniastosłupa trójkątnego prostego (bez przykrywki). Oblicz długość krawędzi podstawy tego pudełka, którego objętość jest największa. Oblicz tę objętość.
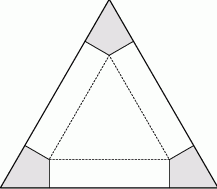
Z kawałka blachy w kształcie sześciokąta foremnego o boku długości 60 cm robimy pudełko o sześciokątnym dnie (otwarte od góry) w następujący sposób: przy każdym wierzchołku odcinamy taki sam deltoid, tnąc w tej samej odległości od wierzchołka raz prostopadle do jednego, a drugi raz do drugiego boku, następnie zaginamy blachę wzdłuż przerywanych linii i lutujemy krawędzie (zobacz rysunek).
Oblicz długość krawędzi podstawy tego pudełka, którego objętość jest największa. Oblicz tę objętość.
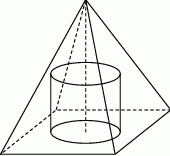
W ostrosłup prawidłowy czworokątny o wysokości 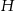 i krawędzi podstawy
i krawędzi podstawy  wpisano walec, którego podstawa zawiera się w podstawie ostrosłupa, i którego oś symetrii pokrywa się z osią symetrii ostrosłupa. Jakie powinny być wymiary tego walca, aby jego objętość była największa możliwa? Oblicz tę największą objętość.
wpisano walec, którego podstawa zawiera się w podstawie ostrosłupa, i którego oś symetrii pokrywa się z osią symetrii ostrosłupa. Jakie powinny być wymiary tego walca, aby jego objętość była największa możliwa? Oblicz tę największą objętość.
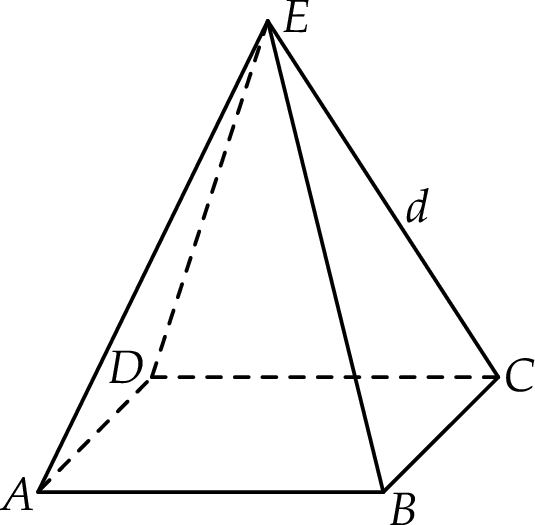
Rozważamy wszystkie ostrosłupy prawidłowe czworokątne 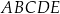 , w których krawędź boczna ma długość
, w których krawędź boczna ma długość 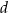 (zobacz rysunek).
(zobacz rysunek).
-
Wyznacz zależność objętości
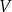 ostrosłupa od jego wysokości
ostrosłupa od jego wysokości 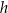 i podaj dziedzinę funkcji
i podaj dziedzinę funkcji 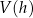 .
. -
Wyznacz wysokość tego z rozważanych ostrosłupów, którego objętość jest największa.
Suma długości wszystkich krawędzi prostopadłościanu jest równa 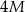 , a jedna z jego ścian na pole powierzchni dwa razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
, a jedna z jego ścian na pole powierzchni dwa razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
Suma długości wszystkich krawędzi prostopadłościanu jest równa 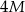 , a jedna z jego ścian na pole powierzchni trzy razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
, a jedna z jego ścian na pole powierzchni trzy razy większe od innej ściany tego prostopadłościanu. Oblicz jaka jest powierzchnia całkowita tego prostopadłościanu, jeżeli jego objętość jest największa możliwa.
Tworząca stożka ma długość 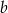 . Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
. Wyznacz wysokość tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.
Rozpatrujemy wszystkie stożki o tworzącej długości 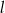 . Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz tę największą objętość.
. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz tę największą objętość.
Rozpatrujemy wszystkie stożki, w których suma sześcianów długości promienia podstawy i wysokości jest równa 12. Wyznacz ten spośród rozpatrywanych stożków, którego objętość jest największa. Oblicz tę objętość.
W stożek, którego wysokość ma długość 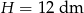 , a promień jego podstawy ma długość
, a promień jego podstawy ma długość 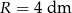 wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
wpisano walec, o podstawach równoległych do podstawy stożka. Jakie powinny być wymiary walca, aby jego objętość była największa?
Suma długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka jest równa 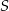 . Długość jednej z tych krawędzi jest dwa razy większa od drugiej. Oblicz promień sfery opisanej na tym z rozważanych prostopadłościanów, którego objętość jest największa.
. Długość jednej z tych krawędzi jest dwa razy większa od drugiej. Oblicz promień sfery opisanej na tym z rozważanych prostopadłościanów, którego objętość jest największa.

