W czworościanie, którego wszystkie krawędzie mają taką samą długość 6, umieszczono kulę tak, że ma ona dokładnie jeden punkt wspólny z każdą ścianą czworościanu. Płaszczyzna 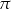 , równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej
, równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej 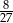 objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka
objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka 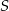 kuli od płaszczyzny
kuli od płaszczyzny 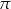 , tj. długość najkrótszego spośród odcinków
, tj. długość najkrótszego spośród odcinków 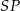 , gdzie
, gdzie 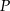 jest punktem płaszczyzny
jest punktem płaszczyzny 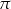 .
.
/Szkoła średnia/Geometria/Stereometria/Czworościan foremny
Czworościan foremny o krawędzi  rozcięto płaszczyzną prostopadłą do jednej z krawędzi, przechodzącą w odległości
rozcięto płaszczyzną prostopadłą do jednej z krawędzi, przechodzącą w odległości 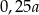 od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.
od jednego końca tej krawędzi. Oblicz objętość otrzymanych brył.
Oblicz cosinus kąta jaki tworzą dwie ściany czworościanu foremnego. Podaj przybliżoną miarę tego kąta.
Oto w jaki sposób można uzasadnić, że suma odległości dowolnego punktu 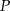 wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
wewnątrz trójkąta równobocznego od boków tego trójkąta jest stała, tzn. nie zależy od wyboru tego punktu.
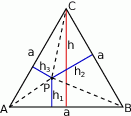
- Łączymy punkt
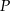 z wierzchołkami trójkąta i zapisujemy równość pól
z wierzchołkami trójkąta i zapisujemy równość pól 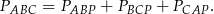
- Korzystamy ze wzoru na pole trójkąta
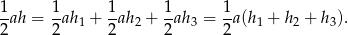
- Wnioskujemy, że
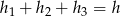 , a więc suma ta nie zależy od wyboru punktu
, a więc suma ta nie zależy od wyboru punktu 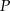 .
.
Postępując w analogiczny sposób wykaż, że suma odległości dowolnego punktu 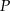 wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu
wewnątrz czworościanu foremnego od jego ścian jest stała, to znaczy nie zależy od wyboru punktu 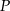 .
.
Czworościan foremny przecięto płaszczyzną przechodzącą przez krawędź boczną i wysokość podstawy. Jako przekrój otrzymano trójkąt o polu równym 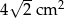 . Oblicz objętość tego czworościanu.
. Oblicz objętość tego czworościanu.
Czworościan foremny przecięto płaszczyzną 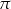 styczną do kuli wpisanej w ten czworościan (tzn. kuli stycznej do wszystkich ścian czworościanu) oraz równoległą do jednej ze ścian czworościanu. Oblicz stosunek objętości brył, na które płaszczyzna
styczną do kuli wpisanej w ten czworościan (tzn. kuli stycznej do wszystkich ścian czworościanu) oraz równoległą do jednej ze ścian czworościanu. Oblicz stosunek objętości brył, na które płaszczyzna 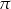 podzieliła czworościan.
podzieliła czworościan.
Oblicz promień kuli stycznej do wszystkich krawędzi czworościanu foremnego o krawędzi długości  .
.
Środki ścian czworościanu foremnego 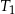 są wierzchołkami czworościanu
są wierzchołkami czworościanu 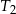 . Oblicz stosunek objętości czworościanów
. Oblicz stosunek objętości czworościanów 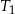 i
i 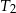 .
.
Oblicz objętość czworościanu foremnego o krawędzi  .
.
Wysokość czworościanu foremnego ma długość 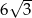 . Oblicz jego objętość i pole powierzchni całkowitej.
. Oblicz jego objętość i pole powierzchni całkowitej.
Oblicz długość odcinka łączącego środki przeciwległych krawędzi czworościanu foremnego o krawędzi długości  .
.
Oblicz stosunek objętości kuli wpisanej w czworościan foremny do objętości kuli opisanej na tym czworościanie.
We wnętrzu sześcianu umieszczono czworościan foremny w ten sposób, że wszystkie krawędzie czworościanu są przekątnymi ścian bocznych sześcianu. Wyznacz stosunek objętości czworościanu do objętości sześcianu.

