Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Ciągi/Arytmetyczny/W geometrii/Różne

Wyszukiwanie zadań

Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz długości jego boków, jeśli obwód prostokąta jest równy 14.

Ukryj Podobne zadania

Długości boków prostokąta i długość jego przekątnej tworzą ciąg arytmetyczny. Oblicz długości jego boków, jeśli pole prostokąta jest równe 48.

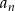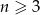Niech an , dla n ≥ 3 będzie liczbą krawędzi graniastosłupa prostego o podstawie będącej n -kątem foremnym.

  • Wyznacz wzór ciągu (an ) .
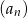  • Sprawdź czy ciąg 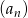(a ) n jest ciągiem arytmetycznym.
  • Uzasadnij, że żaden wyraz tego ciągu nie jest równy 2009.

Obwód trapezu równoramiennego wynosi 116. Oblicz pole tego trapezu, jeśli długości ramienia i podstaw trapezu są (w podanej kolejności) trzema kolejnymi wyrazami ciągu arytmetycznego oraz długość odcinka łączącego środki ramion trapezu wynosi 41.

Długości boków trójkąta 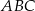ABC są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę 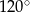120∘ . Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta 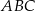ABC jest równa 840. Oblicz objętość największej kuli jaka może być umieszczona wewnątrz tego prostopadłościanu.

Miary kątów wielokąta tworzą ciąg arytmetyczny, którego różnica jest równa 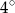4∘ . Największy kąt ma miarę 172∘ .

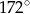  • Ile boków ma ten wielokąt?
  • Ile ma przekątnych?

Ania układa szklane kulki w figury pokazane na rysunku, na którym pokazane są pierwsze trzy figury.

PIC

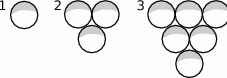
  • Niech 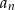an będzie różnicą liczby kulek w 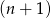(n + 1) –ej i n –tej figurze. Wypisz pierwszych 5 wyrazów ciągu (a ) n .
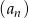  • Uzasadnij, że 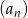(an) jest ciągiem arytmetycznym i oblicz ile potrzeba kulek do ułożenia 20 figury.

Krawędzie prostopadłościanu wychodzące z jednego wierzchołka tworzą ciąg arytmetyczny o pierwszym wyrazie 5 i różnicy 2. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.

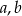Długość krawędzi bocznej c prostopadłościennego pudełka o podstawie prostokąta tworzy wraz z długościami krawędzi podstawy a,b (w kolejności 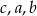c,a,b ) ciąg artymetyczny o różnicy -2.

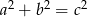  • Oblicz długości krawędzi pudełka, jeśli a2 + b 2 = c2 .
  • Wyznacz miarę kąta nachylenia przekątnej pudełka do płaszczyzny podstawy.

Miary pięciu kątów tworzą ciąg arytmetyczny. Drugim wyrazem tego ciągu jest 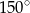15 0∘ , a czwartym 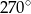270∘ . Oblicz sumę sinusów tych pięciu kątów.

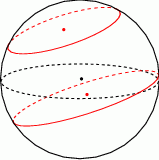
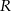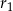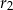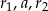Kulę o promieniu R przecięto dwiema równoległymi płaszczyznami w sposób przedstawiony na poniższym rysunku. Przekroje mają promienie r1 oraz r2 i są odległe od siebie o a . Liczby r1,a,r2 w podanej kolejności tworzą trzywyrazowy ciąg arytmetyczny, którego różnica jest równa 1. Suma wyrazów tego ciągu jest równa 18. Znajdź długość promienia kuli.

PIC

Miary kątów trójkąta prostokątnego tworzą ciąg arytmetyczny. Jeśli trójkąt ten będziemy obracać wokół dłuższej przyprostokątnej, to otrzymamy stożek, którego pole powierzchni bocznej wynosi 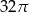32π . Oblicz długości boków tego trójkąta.