- Zaznacz w układzie współrzędnych zbiór
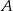 punktów, których współrzędne
punktów, których współrzędne 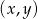 spełniają warunek:
spełniają warunek: 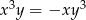 .
. - Wiedząc, że wykres funkcji homograficznej
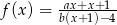 nie ma punktów wspólnych ze zbiorem
nie ma punktów wspólnych ze zbiorem 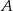 wyznacz
wyznacz  i
i 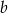 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
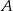 punktów, których współrzędne
punktów, których współrzędne 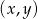 spełniają warunek:
spełniają warunek: 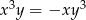 .
. 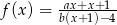 nie ma punktów wspólnych ze zbiorem
nie ma punktów wspólnych ze zbiorem 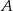 wyznacz
wyznacz  i
i 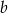 .
.
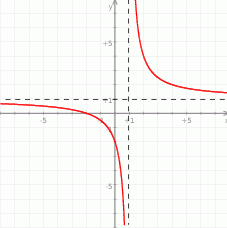
W oparciu o wykres funkcji określonej wzorem 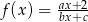 , wyznacz
, wyznacz 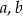 i
i  .
.
Dane są funkcje 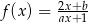 oraz
oraz 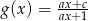 , o których wiadomo, że ich wykresy mają punkt wspólny
, o których wiadomo, że ich wykresy mają punkt wspólny 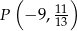 , a miejscem zerowym funkcji
, a miejscem zerowym funkcji 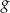 jest liczba:
jest liczba: 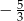 . Wyznacz wartości parametrów
. Wyznacz wartości parametrów 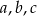 .
.
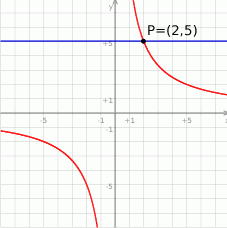
Rysunek przedstawia fragment wykresu funkcji 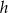 , określonej wzorem
, określonej wzorem 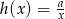 dla
dla 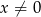 . Wiadomo, że do wykresu funkcji
. Wiadomo, że do wykresu funkcji 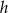 należy punkt
należy punkt 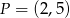 .
.
 .
. 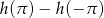 jest dodatnia czy ujemna.
jest dodatnia czy ujemna. 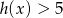 .
.Punkt 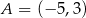 jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem
jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem 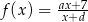 , gdy
, gdy 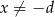 . Oblicz iloraz
. Oblicz iloraz 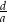 .
.
Punkt 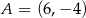 jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem
jest środkiem symetrii wykresu funkcji homograficznej określonej wzorem 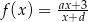 , gdy
, gdy 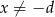 . Oblicz iloraz
. Oblicz iloraz 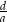 .
.
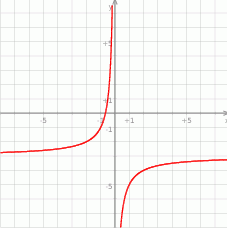
Rysunek przedstawia fragment wykresu funkcji określonej wzorem 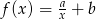 dla
dla 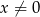 .
.
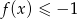 .
.  i
i 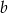 .
.Na rysunku przedstawiono fragment wykresu funkcji 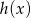 otrzymanego przez przesunięcie o wektor
otrzymanego przez przesunięcie o wektor ![[2,1]](https://img.zadania.info/zad/9337096/HzadT1x.gif) wykresu funkcji
wykresu funkcji 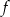 określonej wzorem
określonej wzorem 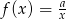 , dla
, dla 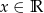 i
i 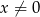 .
.
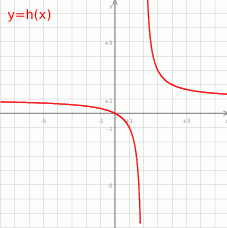
Wyznacz wzór funkcji 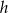 , a następnie sprawdź, czy punkt
, a następnie sprawdź, czy punkt 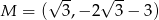 należy do jej wykresu.
należy do jej wykresu.
Wykres funkcji homograficznej 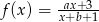 można otrzymać przesuwając wykres funkcji
można otrzymać przesuwając wykres funkcji 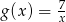 , a dziedzina funkcji
, a dziedzina funkcji 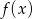 jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki
jest tym samym zbiorem co jej zbiór wartości. Wyznacz współczynniki  i
i 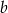 .
.
