Każde dwa spośród trzech okręgów są zewnętrznie styczne. Oblicz promienie tych okręgów, jeśli wiadomo, że odległości między ich środkami wynoszą 8, 11, 13.
/Szkoła średnia/Geometria/Planimetria/Okrąg i koło/Styczność/Trzy okręgi styczne
W półkole o średnicy 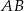 wpisano okrąg styczny do średnicy
wpisano okrąg styczny do średnicy 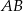 w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu
w jej środku. Znajdź promień okręgu stycznego jednocześnie do półokręgu 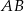 , do wpisanego okręgu oraz do średnicy
, do wpisanego okręgu oraz do średnicy 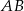 jeżeli
jeżeli 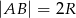 .
.
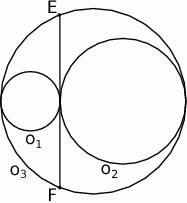
Okręgi 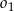 i
i 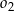 są styczne zewnętrznie oraz oba są styczne wewnętrznie do okręgu
są styczne zewnętrznie oraz oba są styczne wewnętrznie do okręgu 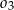 . Środki wszystkich trzech okręgów leżą na jednej prostej, a cięciwa
. Środki wszystkich trzech okręgów leżą na jednej prostej, a cięciwa 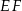 okręgu
okręgu 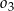 jest wspólną styczną okręgów
jest wspólną styczną okręgów 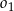 i
i 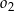 . Oblicz długość odcinka
. Oblicz długość odcinka 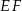 jeżeli promienie okręgów
jeżeli promienie okręgów 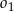 i
i 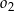 są odpowiednio równe
są odpowiednio równe 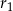 i
i 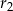 .
.
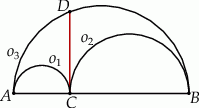
Na średnicy 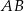 półokręgu
półokręgu 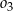 wybrano punkt
wybrano punkt 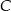 i na odcinkach
i na odcinkach 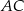 i
i 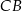 jako na średnicach skonstruowano półokręgi
jako na średnicach skonstruowano półokręgi 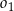 i
i 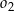 . Odcinek
. Odcinek 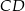 jest odcinkiem wspólnej stycznej półokręgów
jest odcinkiem wspólnej stycznej półokręgów 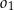 i
i 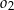 . Oblicz długość odcinka
. Oblicz długość odcinka 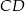 jeżeli promienie półokręgów
jeżeli promienie półokręgów 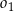 i
i 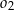 są odpowiednio równe
są odpowiednio równe 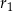 i
i 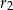 .
.
Dwa styczne zewnętrznie okręgi o środkach 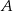 i
i 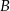 są styczne wewnętrznie do okręgu
są styczne wewnętrznie do okręgu 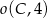 , przy czym punkty
, przy czym punkty 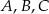 nie są współliniowe. Oblicz obwód trójkąta
nie są współliniowe. Oblicz obwód trójkąta 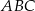 .
.
Dane dwa okręgi o środkach 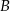 i
i 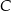 są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie
są styczne zewnętrznie i jednocześnie są styczne wewnętrznie do okręgu o środku w punkcie 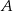 . Wiedząc, że
. Wiedząc, że 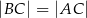 oraz promień okręgu o środku
oraz promień okręgu o środku 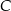 ma długość
ma długość 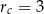 oblicz długość odcinka
oblicz długość odcinka 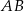 .
.
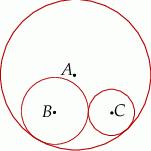
Dane są dwa okręgi zewnętrznie styczne oraz styczne wewnętrznie do trzeciego. Środki okręgów tworzą trójkąt równoramienny o bokach długości 1 i 2. Znajdź długości promieni tych okręgów (rozważ dwa przypadki).
Trzy okręgi o promieniach 2, 4 i 6 są parami zewnętrznie styczne. Oblicz długość promienia okręgu zawierającego punkty styczności tych okręgów.
Trzy koła o promieniu 1 są parami styczne zewnętrznie. Oblicz pole obszaru zawartego między tymi kołami.
Dane są okręgi o środkach 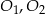 oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku
oraz promieniu 2. Jeden z nich jest styczny wewnętrznie, a drugi styczny zewnętrznie do okręgu o środku 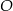 i promieniu 5. Wiadomo, że
i promieniu 5. Wiadomo, że 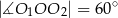 . Oblicz długość odcinka
. Oblicz długość odcinka 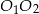 .
.
Okręgi 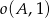 ,
, 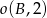 i
i 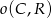 są parami styczne zewnętrznie. Oblicz
są parami styczne zewnętrznie. Oblicz 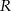 , jeśli
, jeśli 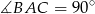 .
.
Dane są trzy okręgi o środkach 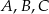 i promieniach równych odpowiednio
i promieniach równych odpowiednio 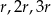 . Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie
. Każde dwa z tych okręgów są zewnętrznie styczne: pierwszy z drugim w punkcie 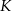 , drugi z trzecim w punkcie
, drugi z trzecim w punkcie 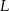 i trzeci z pierwszym w punkcie
i trzeci z pierwszym w punkcie 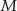 . Oblicz stosunek pola trójkąta
. Oblicz stosunek pola trójkąta 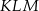 do pola trójkąta
do pola trójkąta 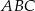 .
.

