Najmniejszą liczbą całkowitą spełniającą nierówność 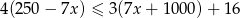 jest
jest
A) 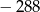 B)
B) 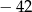 C)
C) 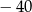 D)
D) 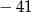
/Szkoła średnia/Zadania testowe
Najmniejszą liczbą całkowitą spełniającą nierówność 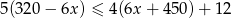 jest
jest
A) 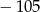 B)
B) 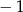 C)
C) 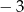 D)
D) 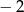
Równanie 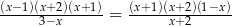
A) ma cztery różne rozwiązania: 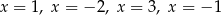 .
.
B) ma trzy różne rozwiązania: 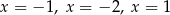 .
.
C) ma dwa różne rozwiązania: 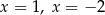 .
.
D) ma dwa różne rozwiązania: 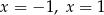 .
.
Wierzchołek paraboli będącej wykresem funkcji 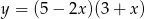 ma współrzędne
ma współrzędne
A) 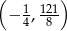 B)
B) 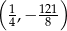 C)
C) 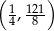 D)
D) 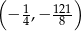
Wierzchołek paraboli będącej wykresem funkcji 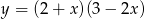 ma współrzędne
ma współrzędne
A) 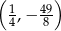 B)
B) 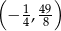 C)
C) 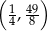 D)
D) 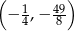
Do wykresu funkcji liniowej 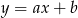 należą punkty
należą punkty 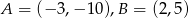 . Wynika stąd, że
. Wynika stąd, że
A) 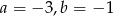 B)
B) 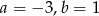 C)
C) 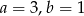 D)
D) 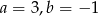
Jeżeli wiadomo, że punkty 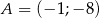 i
i 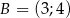 należą do wykresu funkcji liniowej, to ta funkcja opisana jest wzorem
należą do wykresu funkcji liniowej, to ta funkcja opisana jest wzorem
A) 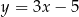 B)
B) 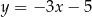 C)
C) 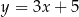 D)
D) 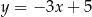
Do wykresu funkcji liniowej 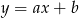 należą punkty
należą punkty 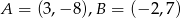 . Wynika stąd, że
. Wynika stąd, że
A) 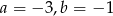 B)
B) 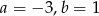 C)
C) 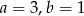 D)
D) 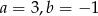
Do wykresu funkcji liniowej 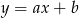 należą punkty
należą punkty 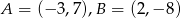 . Wynika stąd, że
. Wynika stąd, że
A) 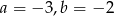 B)
B) 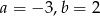 C)
C) 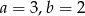 D)
D) 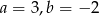
Do wykresu funkcji liniowej należą punkty 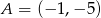 ,
, 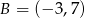 , zatem funkcja liniowa ma wzór
, zatem funkcja liniowa ma wzór
A) 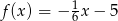 B)
B) 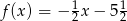 C)
C) 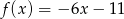 D)
D) 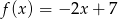
Liczba krawędzi graniastosłupa jest o 10 większa od liczby jego ścian. Ile wierzchołków ma ten graniastosłup?
A) 6 B) 18 C) 24 D) 12
Liczba krawędzi graniastosłupa jest o 8 większa od liczby jego ścian. Ile wierzchołków ma ten graniastosłup?
A) 5 B) 15 C) 10 D) 16
Liczba wszystkich krawędzi graniastosłupa jest o 10 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
Liczba wszystkich krawędzi graniastosłupa jest o 12 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
W trapezie prostokątnym podstawy mają długości 6 i 9. Która z liczb nie może być długością dłuższego ramienia trapezu?
A) 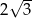 B)
B) 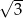 C)
C) 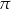 D)
D) 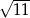
Dany jest ciąg 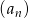 o wyrazie ogólnym
o wyrazie ogólnym 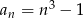 , gdzie
, gdzie 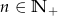 . Wówczas:
. Wówczas:
A) 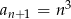 B)
B) 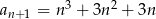 C)
C) 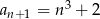 D)
D) 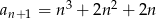
Dany jest ciąg 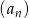 o wyrazie ogólnym
o wyrazie ogólnym 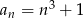 , gdzie
, gdzie 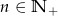 . Wówczas:
. Wówczas:
A) 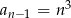 B)
B) 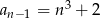 C)
C) 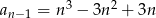 D)
D) 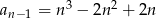
Dany jest ciąg 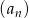 o wyrazie ogólnym
o wyrazie ogólnym 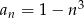 , gdzie
, gdzie 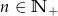 . Wówczas:
. Wówczas:
A) 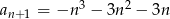
B) 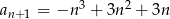
C) 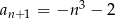
D) 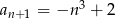
Trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy -2. Pierwszy wyraz tego ciągu jest równy
A) 16 B) -16 C) 8 D) -8
W ciągu geometrycznym 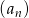 mamy
mamy 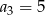 i
i 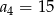 . Wtedy wyraz
. Wtedy wyraz 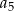 jest równy
jest równy
A) 10 B) 20 C) 75 D) 45
W ciągu geometrycznym 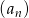 , gdzie
, gdzie 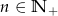 dane są:
dane są: 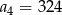 i
i 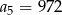 . Zatem:
. Zatem:
A) 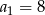 B)
B) 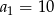 C)
C) 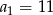 D)
D) 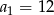
Dany jest nieskończony ciąg geometryczny 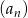 , w którym
, w którym 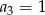 i
i 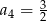 . Wtedy
. Wtedy
A) 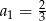 B)
B) 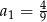 C)
C) 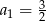 D)
D) 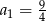
W ciągu geometrycznym 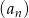 mamy
mamy 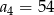 i
i 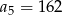 . Wtedy wyraz
. Wtedy wyraz 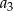 jest równy
jest równy
A) 6 B) 18 C) 2 D) 27
Trzeci wyraz ciągu geometrycznego jest równy 6, a czwarty wyraz tego ciągu jest równy -2. Pierwszy wyraz tego ciągu jest równy
A) 27 B) -27 C) 54 D) -54
Dany jest nieskończony ciąg geometryczny 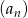 , w którym
, w którym 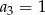 i
i 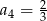 . Wtedy
. Wtedy
A) 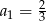 B)
B) 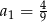 C)
C) 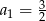 D)
D) 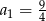
Jeśli trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy 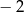 , to drugi wyraz jest równy
, to drugi wyraz jest równy
A) 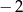 B) 2 C)
B) 2 C) 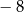 D) 8
D) 8
Kąt rozwarcia stożka ma miarę 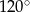 , a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
A) 3 B) 6 C) 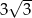 D)
D) 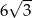
Kąt rozwarcia stożka ma miarę 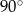 , a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
A) 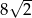 B) 4 C)
B) 4 C) 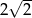 D)
D) 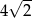
Wykresem funkcji 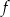 danej wzorem
danej wzorem 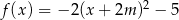 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 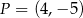 . Wówczas
. Wówczas
A) 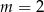 B)
B) 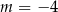 C)
C) 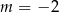 D)
D) 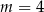
Dwa boki trójkąta 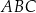 są zawarte w prostych
są zawarte w prostych 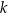 i
i 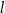 o równaniach
o równaniach
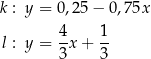
Trójkąt 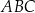
| A) jest prostokątny | B) nie jest prostokątny |
i jeden z jego wierzchołków może mieć współrzędne
1. 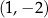 | 2. 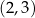 | 3.  |
Wykonując rozmowę telefoniczną płacimy 63 grosze za rozpoczęcie połączenia oraz 42 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 16,17 zł?
A) 38 B) 36 C) 43 D) 37
Wykonując rozmowę telefoniczną płacimy 43 grosze za rozpoczęcie połączenia oraz 32 grosze za każdą minutę połączenia. Ile minut trwała rozmowa, której łączny koszt wyniósł 12,59 zł?
A) 39 B) 37 C) 38 D) 44
W trójkącie równoramiennym o polu 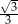 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 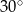 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) wymierną mniejszą od 2 B) niewymierną większą o 1
C) całkowitą większą od 1 D) niewymierną mniejszą od 2
W trójkącie równoramiennym o polu 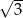 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 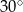 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) wymierną mniejszą od 3 B) niewymierną większą o 3
C) całkowitą większą od 3 D) niewymierną mniejszą od 3
W trójkącie równoramiennym o polu 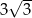 miara kąta przy podstawie jest równa
miara kąta przy podstawie jest równa 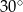 . Długość podstawy tego trójkąta jest liczbą
. Długość podstawy tego trójkąta jest liczbą
A) całkowitą większą od 4 B) niewymierną większą o 4
C) wymierną mniejszą od 4 D) niewymierną mniejszą od 4
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 2 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 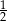 B)
B) 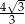 C) 1 D)
C) 1 D) 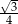
Wysokość ściany bocznej ostrosłupa prawidłowego sześciokątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej tego ostrosłupa do pola jego podstawy jest równy
A) 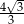 B)
B) 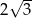 C)
C) 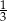 D)
D) 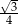
Nieskończony malejący ciąg geometryczny 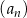 , określony dla
, określony dla 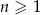 , spełnia warunki:
, spełnia warunki:
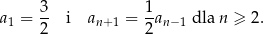
Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 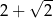 C)
C) 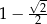 D)
D) 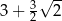
Dane są wielomiany 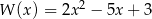 i
i 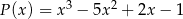 . Wielomian
. Wielomian 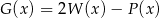 jest równy
jest równy
A) 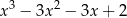 B)
B) 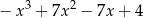
C) 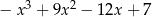 D)
D) 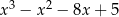
Dane są wielomiany 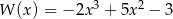 oraz
oraz 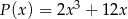 . Wielomian
. Wielomian 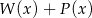 jest równy
jest równy
A) 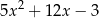 B)
B) 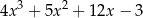
C) 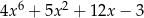 D)
D) 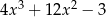
Dane są wielomiany 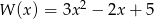 oraz
oraz 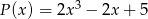 . Wielomian
. Wielomian 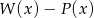 jest równy
jest równy
A) 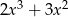 B)
B) 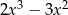 C)
C) 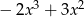 D)
D) 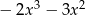
Dane są wielomiany 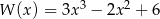 oraz
oraz 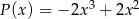 . Wielomian
. Wielomian 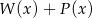 jest równy
jest równy
A) 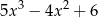 B)
B) 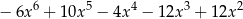
C) 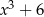 D)
D) 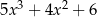
Dane są wielomiany 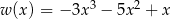 i
i 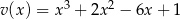 . Wówczas wielomian
. Wówczas wielomian 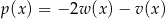 jest równy:
jest równy:
A) 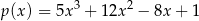 B)
B) 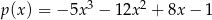
C) 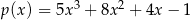 D)
D) 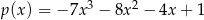
Dane są wielomiany 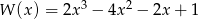 i
i 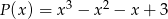 . Wielomian
. Wielomian 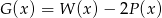 jest równy
jest równy
A) 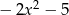 B)
B) 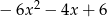 C)
C) 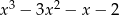 D)
D) 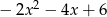
Dane są wielomiany 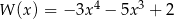 oraz
oraz 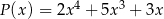 . Wielomian
. Wielomian 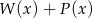 jest równy
jest równy
A) 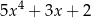 B)
B) 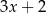
C) 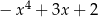 D)
D) 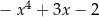
Liczby dodatnie 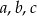 spełniają warunki
spełniają warunki 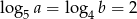 i
i 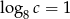 . Wtedy liczba
. Wtedy liczba 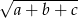 jest równa
jest równa
A) 7 B) 17 C) 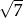 D) 2
D) 2
Liczby dodatnie 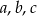 spełniają warunki
spełniają warunki 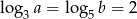 i
i 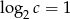 . Wtedy liczba
. Wtedy liczba 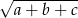 jest równa
jest równa
A) 7 B) 6 C) 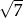 D) 2
D) 2
Liczby dodatnie 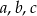 spełniają warunki
spełniają warunki 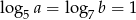 i
i 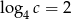 . Wtedy liczba
. Wtedy liczba 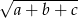 jest równa
jest równa
A) 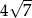 B) 28 C)
B) 28 C) 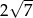 D) 2
D) 2
Liczba 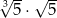 jest równa
jest równa
A) 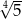 B)
B) 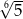 C)
C) 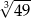 D)
D) 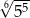
Liczba 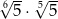 jest równa liczbie
jest równa liczbie
A) 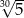 B)
B) 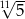 C)
C) 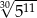 D)
D) 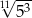
Liczba 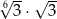 jest równa
jest równa
A) 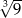 B)
B) 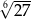 C)
C) 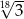 D)
D) 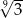
Liczba 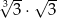 jest równa
jest równa
A) 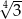 B)
B) 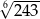 C)
C) 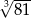 D)
D) 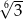
Liczba 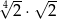 jest równa
jest równa
A) 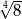 B)
B) 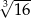 C)
C) 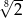 D)
D) 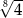
W ciągu geometrycznym 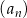 , określonym dla
, określonym dla 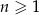 , wszystkie wyrazy są niezerowe, oraz iloczyn
, wszystkie wyrazy są niezerowe, oraz iloczyn 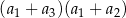 jest trzy razy mniejszy od pierwszego wyrazu tego ciągu. Suma czterech początkowych wyrazów ciągu
jest trzy razy mniejszy od pierwszego wyrazu tego ciągu. Suma czterech początkowych wyrazów ciągu 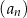 jest równa
jest równa
A) 3 B) 1 C) 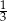 D) 9
D) 9
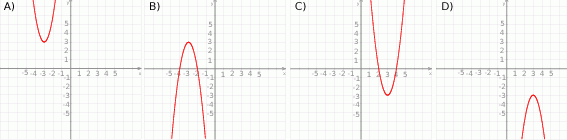
Zbiorem wartości funkcji kwadratowej 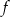 jest przedział
jest przedział 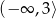 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 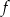 ?
?
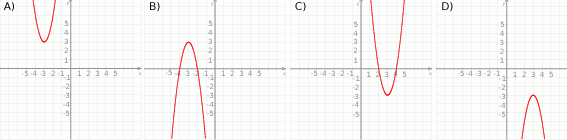
Zbiorem wartości funkcji kwadratowej  jest przedział
jest przedział  . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji  ?
?
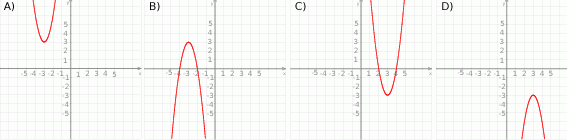
Wskaż fragment wykresu funkcji kwadratowej, której zbiorem wartości jest 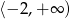 .
.
Zbiorem wartości funkcji kwadratowej 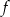 jest przedział
jest przedział 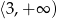 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 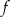 ?
?
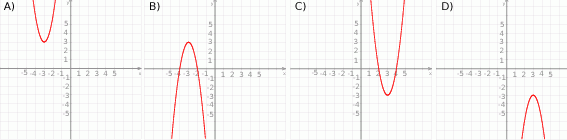
Zbiorem wartości funkcji kwadratowej 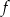 jest przedział
jest przedział 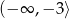 . Na którym rysunku przedstawiono wykres funkcji
. Na którym rysunku przedstawiono wykres funkcji 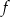 ?
?