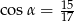Ciąg 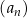 określony wzorem
określony wzorem 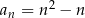 dla każdej liczby naturalnej
dla każdej liczby naturalnej 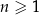 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 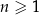
1) różnica 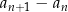 jest liczbą ujemną. jest liczbą ujemną. |
2) różnica 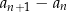 jest równa zero. jest równa zero. |
3) różnica 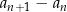 jest liczbą dodatnią. jest liczbą dodatnią. |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 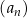 określony wzorem
określony wzorem 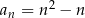 dla każdej liczby naturalnej
dla każdej liczby naturalnej 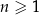 jest
jest
| A) rosnący, | B) malejący, | C) stały, |
ponieważ dla każdej liczby naturalnej 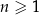
1) różnica 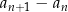 jest liczbą ujemną. jest liczbą ujemną. |
2) różnica 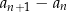 jest równa zero. jest równa zero. |
3) różnica 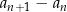 jest liczbą dodatnią. jest liczbą dodatnią. |
Wyrażenie 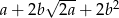 może być przekształcone do postaci
może być przekształcone do postaci
A) 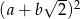 B)
B) 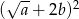 C)
C) 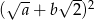 D)
D) 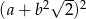
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była czarna. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z pierwszej z tych urn, jest równe
A) 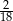 B)
B) 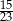 C)
C) 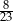 D)
D) 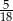
Dane są dwie urny z kulami. W pierwszej urnie jest 10 kul: 8 białych i 2 czarne, w drugiej jest 8 kul: 5 białych i 3 czarne. Wylosowanie każdej z urn jest jednakowo prawdopodobne. Wylosowano jedną z tych urn i wyciągnięto z niej losowo jedną kulę. Wyciągnięta kula była biała. Prawdopodobieństwo zdarzenia, że wylosowana kula pochodziła z drugiej z tych urn, jest równe
A) 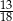 B)
B) 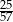 C)
C) 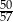 D)
D) 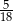
Punkt 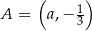 należy do wykresu funkcji liniowej
należy do wykresu funkcji liniowej 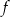 określonej wzorem
określonej wzorem 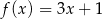 . Wynika stąd, że
. Wynika stąd, że
A) 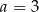 B)
B) 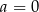 C)
C) 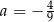 D)
D) 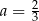
Liczba 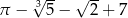 jest rozwiązaniem równania
jest rozwiązaniem równania 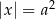 z niewiadomą
z niewiadomą  . Która z podanych liczb jest również rozwiązaniem tego równania?
. Która z podanych liczb jest również rozwiązaniem tego równania?
A) 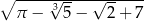 B)
B) 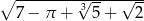
C) 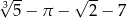 D)
D) 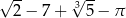
Funkcje liniowe 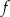 oraz
oraz 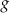 , określone wzorami
, określone wzorami 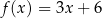 oraz
oraz 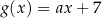 , mają to samo miejsce zerowe. Współczynnik
, mają to samo miejsce zerowe. Współczynnik  we wzorze funkcji
we wzorze funkcji 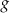 jest równy
jest równy
A) 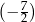 B)
B) 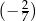 C)
C)  D)
D) 
Niech 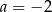 i
i 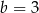 . Wartość wyrażenia
. Wartość wyrażenia 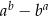 jest równa
jest równa
A) 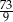 B)
B) 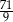 C)
C) 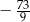 D)
D) 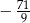
Niech 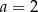 i
i 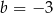 . Wartość wyrażenia
. Wartość wyrażenia 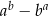 jest równa
jest równa
A) 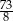 B)
B) 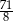 C)
C) 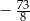 D)
D) 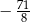
Niech 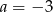 i
i 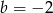 . Wartość wyrażenia
. Wartość wyrażenia 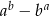 jest równa
jest równa
A) 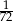 B)
B) 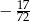 C)
C) 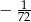 D)
D) 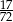
Kąt nachylenia najdłuższej przekątnej graniastosłupa prawidłowego sześciokątnego do płaszczyzny podstawy jest zaznaczony na rysunku
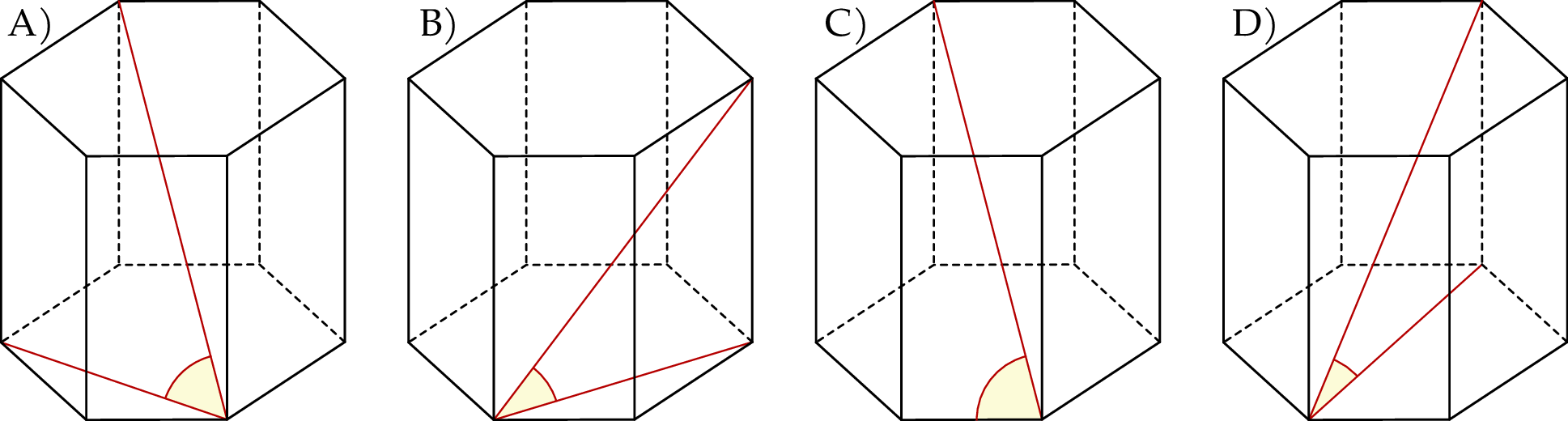
Wykres funkcji kwadratowej 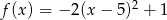 ma dwa punkty wspólne z prostą
ma dwa punkty wspólne z prostą
A) 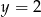 B)
B) 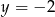 C)
C) 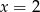 D)
D) 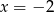
Najdłuższa przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła opisanego na tym sześciokącie jest równe
A) 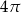 B)
B) 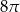 C)
C) 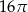 D)
D) 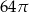
Krótsza przekątna sześciokąta foremnego ma długość 8. Wówczas pole koła wpisanego w ten sześciokąt jest równe
A) 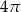 B)
B) 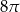 C)
C) 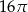 D)
D) 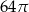
Najdłuższa przekątna sześciokąta foremnego ma długość 6. Wówczas pole koła opisanego na tym sześciokącie jest równe
A) 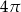 B)
B) 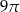 C)
C) 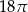 D)
D) 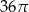
Różnica boków prostokąta jest równa 3, a przekątna tego prostokąta tworzy z jego bokiem kąt o mierze 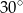 . Krótszy bok prostokąta ma długość
. Krótszy bok prostokąta ma długość
A) 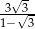 B)
B) 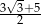 C)
C) 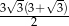 D)
D) 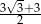
Punkty 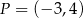 i
i 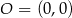 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 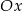 (zobacz rysunek).
(zobacz rysunek).
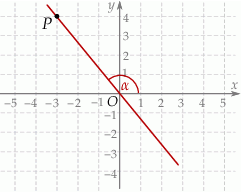
Wtedy tangens kąta  jest równy
jest równy
A) 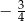 B)
B) 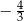 C)
C) 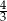 D)
D) 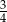
Punkty 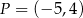 i
i 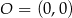 leżą na jednej prostej. Kąt
leżą na jednej prostej. Kąt  jest kątem nachylenia tej prostej do osi
jest kątem nachylenia tej prostej do osi 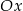 (zobacz rysunek).
(zobacz rysunek).
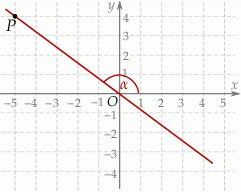
Wtedy tangens kąta  jest równy
jest równy
A)  B)
B)  C)
C) 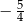 D)
D) 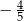
Najmniejszą liczbą całkowitą spełniającą nierówność 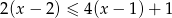 jest
jest
A) 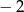 B)
B) 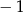 C) 0 D) 1
C) 0 D) 1
Najmniejszą liczbą całkowitą spełniającą nierówność 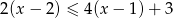 jest
jest
A) 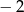 B)
B) 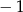 C) 0 D) 1
C) 0 D) 1
Rysunek przedstawia wykres funkcji 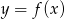 .
.
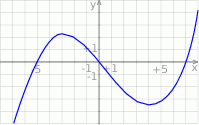
Wskaż wykres funkcji 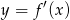 .
.
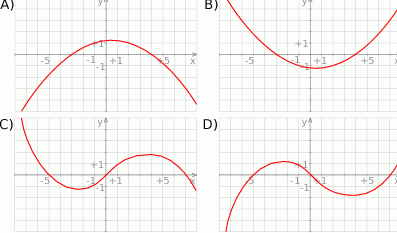
Rysunek przedstawia wykres funkcji 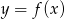 .
.
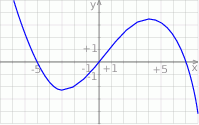
Wskaż wykres funkcji 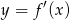 .
.
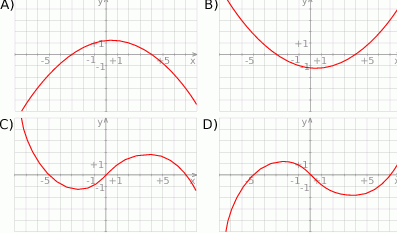
Walec i stożek mają równe promienie podstaw, a wysokość walca jest dwa razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 3 B) 6 C) 2 D) 12
Walec i stożek mają równe promienie podstaw, a wysokość walca jest trzy razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 9 B) 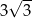 C) 3 D) 27
C) 3 D) 27
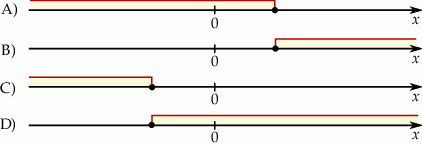
Wskaż rysunek, na którym może być przedstawiony zbiór wszystkich rozwiązań nierówności 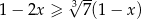 .
.
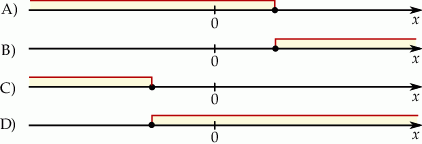
Wskaż rysunek, na którym może być przedstawiony zbiór wszystkich rozwiązań nierówności 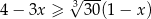 .
.
Punkt 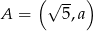 należy do prostej o równaniu
należy do prostej o równaniu 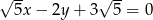 . Wynika stąd, że
. Wynika stąd, że
A) 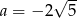 B)
B) 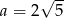 C)
C) 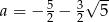 D)
D) 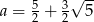
Punkt 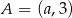 leży na prostej określonej równaniem
leży na prostej określonej równaniem 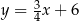 . Stąd wynika, że
. Stąd wynika, że
A) 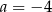 B)
B) 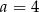 C)
C) 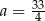 D)
D) 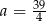
Punkt 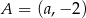 leży na prostej określonej równaniem
leży na prostej określonej równaniem 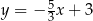 . Stąd wynika, że
. Stąd wynika, że
A) 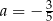 B)
B) 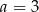 C)
C) 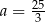 D)
D) 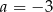
Punkt 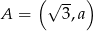 należy do prostej o równaniu
należy do prostej o równaniu 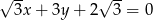 . Wynika stąd, że
. Wynika stąd, że
A) 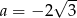 B)
B) 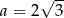 C)
C) 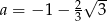 D)
D) 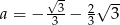
Punkt 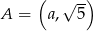 należy do prostej o równaniu
należy do prostej o równaniu 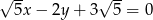 . Wynika stąd, że
. Wynika stąd, że
A) 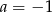 B)
B) 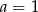 C)
C) 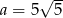 D)
D) 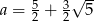
Równość 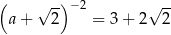 jest prawdziwa dla
jest prawdziwa dla
A) 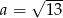 B)
B) 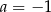 C)
C) 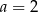 D)
D) 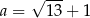
Granica 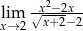 równa jest
równa jest
A) 0 B) 1 C) 8 D) 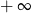
Granica 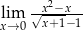 równa jest
równa jest
A) 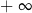 B)
B) 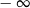 C) 0 D)
C) 0 D) 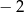
Punkt 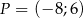 znajduje się na końcowym ramieniu kąta
znajduje się na końcowym ramieniu kąta  (w standardowym położeniu w układzie współrzędnych). Zatem
(w standardowym położeniu w układzie współrzędnych). Zatem 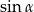 jest równy
jest równy
A) 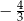 B)
B) 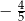 C)
C) 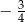 D)
D) 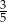
Do prostej należy początek układu współrzędnych oraz punkt 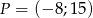 . Wówczas cosinus kąta nachylenia tej prostej do osi
. Wówczas cosinus kąta nachylenia tej prostej do osi 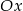 jest równy
jest równy
A) 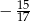 B)
B) 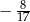 C)
C) 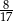 D)
D) 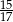
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 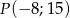 .
.
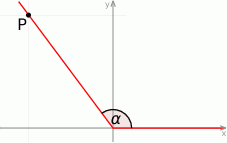
Zatem 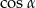 jest równy
jest równy
A) 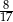 B)
B) 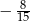 C)
C) 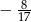 D)
D) 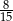
Jedno z ramion kąta  (rysunek) leży na osi odciętych, a drugie przechodzi przez punkt
(rysunek) leży na osi odciętych, a drugie przechodzi przez punkt 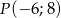 .
.
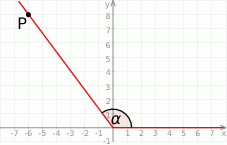
Zatem 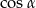 jest równy
jest równy
A) 0,8 B) 0,6 C) 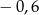 D)
D) 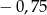
Punkt 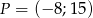 znajduje się na końcowym ramieniu kąta
znajduje się na końcowym ramieniu kąta  . Wówczas
. Wówczas
A) 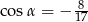 B)
B) 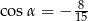 C)
C) 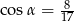 D)
D)