Wielomian 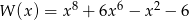 jest równy iloczynowi
jest równy iloczynowi
A) 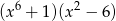 B)
B) 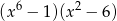 C)
C) 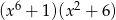 D)
D) 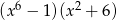
/Szkoła średnia/Zadania testowe
Na rysunku 1 jest przedstawiony wykres funkcji 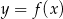 .
.
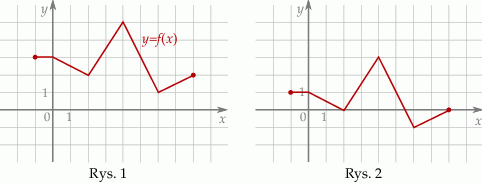
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 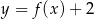 B)
B) 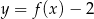 C)
C) 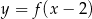 D)
D) 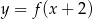
Na rysunku 1 jest przedstawiony wykres funkcji 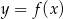 .
.
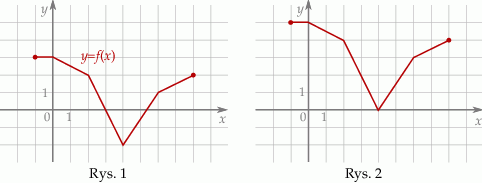
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 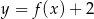 B)
B) 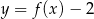 C)
C) 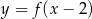 D)
D) 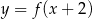
Na poniższych rysunkach przedstawiono wykresy funkcji 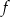 i
i 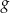 .
.
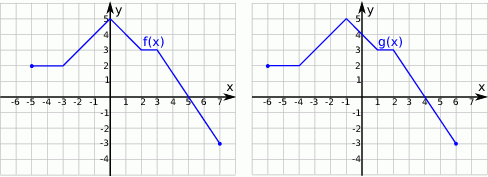
Funkcja 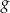 jest określona wzorem
jest określona wzorem
A) 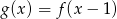 B)
B) 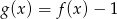 C)
C) 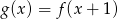 D)
D) 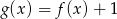
Na poniższych rysunkach przedstawiono wykresy funkcji 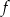 i
i 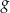 .
.
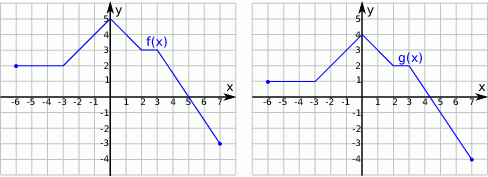
Funkcja 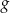 jest określona wzorem
jest określona wzorem
A) 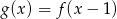 B)
B) 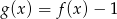 C)
C) 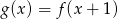 D)
D) 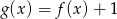
Styczna do wykresu funkcji 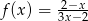 w punkcie o współrzędnych
w punkcie o współrzędnych 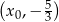 ma równanie
ma równanie
A) 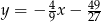 B)
B) 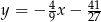 C)
C) 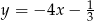 D)
D) 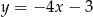
Wszystkie liczby spełniające warunek 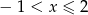 można zapisać za pomocą przedziału:
można zapisać za pomocą przedziału:
A) 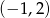 B)
B) 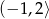 C)
C) 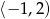 D)
D) 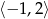
Wszystkie liczby spełniające warunek 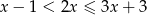 można zapisać za pomocą przedziału:
można zapisać za pomocą przedziału:
A) 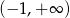 B)
B) 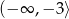 C)
C) 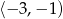 D)
D) 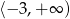
Zbiorem rozwiązań nierówności liniowej 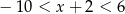 jest przedział liczbowy
jest przedział liczbowy
A) 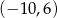 B)
B) 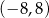 C)
C) 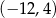 D)
D) 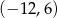
Trapez 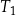 , o polu równym 52 i obwodzie 36, jest podobny do trapezu
, o polu równym 52 i obwodzie 36, jest podobny do trapezu 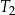 . Pole trapezu
. Pole trapezu 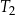 jest równe 13. Obwód trapezu
jest równe 13. Obwód trapezu 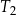 jest równy
jest równy
A) 18 B) 9 C) 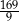 D)
D) 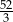
Wierzchołek paraboli 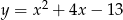 leży na prostej o równaniu
leży na prostej o równaniu
A) 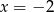 B)
B) 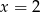 C)
C) 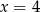 D)
D) 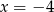
Wierzchołek paraboli 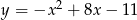 leży na prostej o równaniu
leży na prostej o równaniu
A) 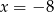 B)
B) 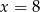 C)
C) 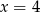 D)
D) 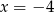
Wierzchołek paraboli 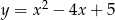 leży na prostej o równaniu
leży na prostej o równaniu
A) 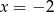 B)
B) 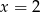 C)
C) 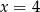 D)
D) 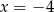
Wykresem funkcji kwadratowej 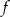 jest parabola o wierzchołku
jest parabola o wierzchołku 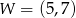 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 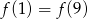 B)
B) 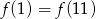 C)
C) 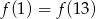 D)
D) 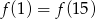
Wykresem funkcji kwadratowej 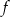 jest parabola o wierzchołku
jest parabola o wierzchołku 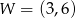 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 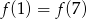 B)
B) 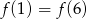 C)
C) 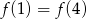 D)
D) 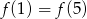
Wykresem funkcji kwadratowej 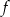 jest parabola o wierzchołku
jest parabola o wierzchołku 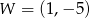 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 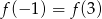 B)
B) 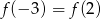 C)
C) 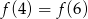 D)
D) 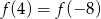
Wykresem funkcji kwadratowej 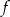 jest parabola o wierzchołku
jest parabola o wierzchołku 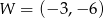 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 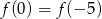 B)
B) 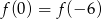 C)
C) 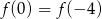 D)
D) 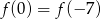
Do kwadratu pewnej liczby rzeczywistej dodano pięciokrotność tej liczby. Która z podanych liczb nie może być wynikiem takiego działania?
A) 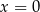 B)
B) 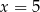 C)
C) 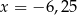 D)
D) 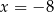
Kula ma objętość 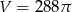 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 6 B) 8 C) 9 D) 12
Kula ma objętość 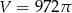 . Promień
. Promień  tej kuli jest równy
tej kuli jest równy
A) 6 B) 8 C) 9 D) 12
Promień kuli o objętości 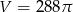 jest równy
jest równy
A) 18 B) 9 C) 8 D) 6
Równanie prostej przechodzącej przez punkty 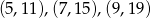 to
to
A) 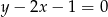 B)
B) 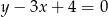 C)
C) 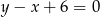 D)
D) 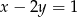
Czworokąt 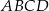 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 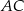 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 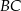 i
i 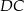 , a kąt
, a kąt 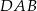 ma miarę
ma miarę 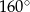 .
.
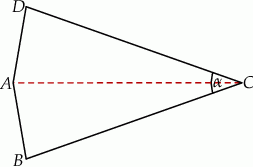
Miara kąta 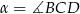 jest równa
jest równa
A) 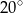 B)
B) 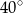 C)
C) 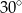 D)
D) 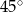
Na rysunku przedstawiono fragment wykresu pewnej funkcji liniowej 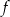 .
.
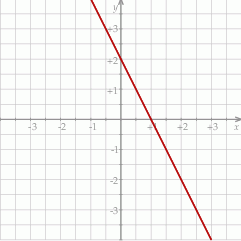
Funkcja liniowa 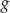 , której wykres jest symetryczny do wykresu funkcji
, której wykres jest symetryczny do wykresu funkcji 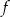 względem poziomej osi układu współrzędnych, jest określona wzorem
względem poziomej osi układu współrzędnych, jest określona wzorem
A) 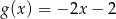 B)
B) 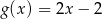 C)
C) 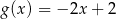 D)
D) 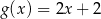
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 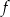 , przy czym
, przy czym 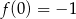 i
i 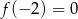 .
.
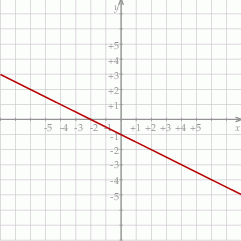
Wykres funkcji 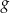 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 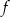 względem początku układu współrzędnych. Funkcja
względem początku układu współrzędnych. Funkcja 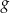 jest określona wzorem
jest określona wzorem
A) 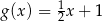 B)
B) 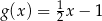 C)
C) 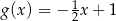 D)
D) 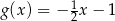
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 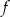 , przy czym
, przy czym 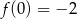 i
i 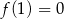 .
.
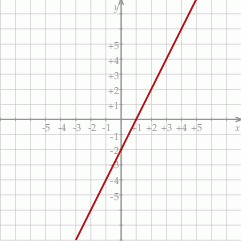
Wykres funkcji 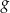 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 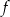 względem początku układu współrzędnych. Funkcja
względem początku układu współrzędnych. Funkcja 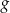 jest określona wzorem
jest określona wzorem
A) 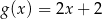 B)
B) 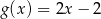 C)
C) 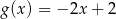 D)
D) 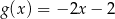
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 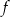 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 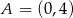 i
i 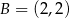 .
.
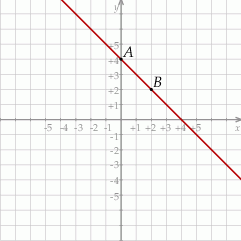
Obrazem prostej 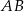 w symetrii względem początku układu współrzędnych jest wykres funkcji
w symetrii względem początku układu współrzędnych jest wykres funkcji 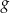 określonej wzorem
określonej wzorem
A) 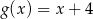 B)
B) 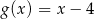 C)
C) 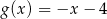 D)
D) 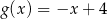
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 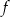 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 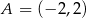 i
i 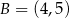 .
.
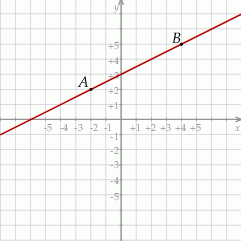
Obrazem prostej 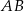 w symetrii względem początku układu współrzędnych jest wykres funkcji
w symetrii względem początku układu współrzędnych jest wykres funkcji 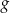 określonej wzorem
określonej wzorem
A) 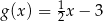 B)
B) 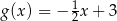 C)
C) 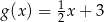 D)
D) 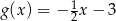
Dana jest funkcja 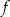 określona wzorem
określona wzorem 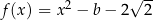 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 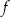 jest
jest 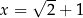 . Współczynnik
. Współczynnik 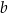 we wzorze funkcji
we wzorze funkcji 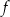 jest równy
jest równy
A) 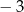 B) 3 C)
B) 3 C) 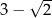 D)
D) 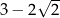
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział największego inwestora?
A) 12% B) 32% C) 48% D) 52%
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział najmniejszego inwestora?
A) 2% B) 4% C) 6% D) 8%
Mamy cztery urny. W urnie o numerze 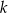 , dla
, dla 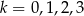 znajduje się
znajduje się 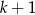 kul białych i
kul białych i 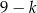 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z
kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z 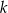 oczkami,
oczkami, 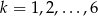 to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby
to losujemy jedną kulę z urny, której numer jest równy reszcie z dzielenia liczby 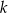 przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
przez 4. Prawdopodobieństwo wylosowania kuli białej jest równe
A) 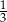 B)
B) 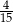 C)
C) 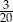 D)
D) 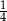
Współczynnikiem liczbowym jednomianu 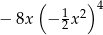 jest liczba
jest liczba
A) 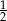 B) 4 C)
B) 4 C) 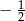 D)
D) 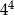
Suma długości krawędzi sześcianu jest równa 60 cm. Długość przekątnej tego sześcianu wynosi
A) 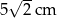 B)
B) 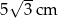 C)
C) 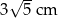 D)
D) 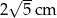
Granica jednostronna 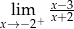
A) nie istnieje B) jest równa 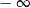 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 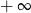
Granica jednostronna 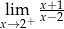
A) nie istnieje B) jest równa 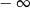 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 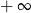
Granica jednostronna 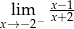
A) jest równa 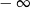 B) jest równa
B) jest równa 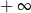 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica jednostronna 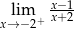
A) jest równa 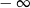 B) jest równa
B) jest równa 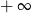 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica jednostronna 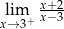
A) jest równa 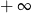 B) jest równa
B) jest równa 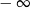 C) nie istnieje D) jest liczbą rzeczywistą
C) nie istnieje D) jest liczbą rzeczywistą
Granica jednostronna 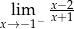
A) jest równa 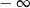 B) jest liczbą rzeczywistą C) nie istnieje D) jest równa
B) jest liczbą rzeczywistą C) nie istnieje D) jest równa 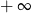
Granica jednostronna 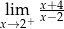
A) nie istnieje B) jest równa 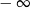 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 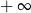
Granica jednostronna 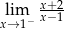
A) nie istnieje B) jest równa 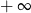 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 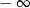
Granica jednostronna 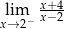
A) jest liczbą rzeczywistą B) nie istnieje C) jest równa 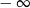 D) jest równa
D) jest równa 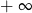
Granica jednostronna 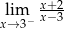
A) jest równa 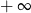 B) jest równa
B) jest równa 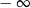 C) nie istnieje D) jest liczbą rzeczywistą
C) nie istnieje D) jest liczbą rzeczywistą
Granica jednostronna 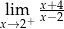
A) jest liczbą rzeczywistą B) nie istnieje C) jest równa 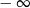 D) jest równa
D) jest równa 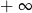
Granica jednostronna 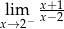
A) nie istnieje B) jest równa 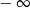 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 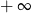
Granica jednostronna 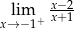
A) jest równa 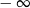 B) jest liczbą rzeczywistą C) nie istnieje D) jest równa
B) jest liczbą rzeczywistą C) nie istnieje D) jest równa 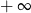
Granica jednostronna 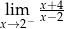
A) nie istnieje B) jest równa 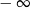 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 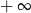
Granica jednostronna 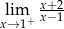
A) nie istnieje B) jest równa 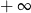 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 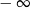
Granica jednostronna 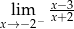
A) nie istnieje B) jest równa 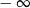 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 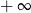
Dana jest funkcja 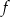 określona wzorem
określona wzorem 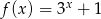 . Wartość funkcji
. Wartość funkcji 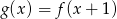 dla argumentu
dla argumentu 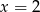 jest równa
jest równa
A) 28 B) 16 C) 25 D) 10
Dana jest funkcja 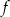 określona wzorem
określona wzorem 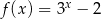 . Wartość funkcji
. Wartość funkcji 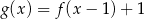 dla argumentu
dla argumentu 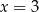 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Dana jest funkcja 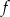 określona wzorem
określona wzorem 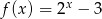 . Wartość funkcji
. Wartość funkcji 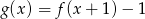 dla argumentu
dla argumentu 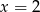 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Liczba 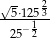 jest równa:
jest równa:
A) 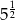 B)
B) 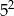 C)
C) 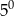 D)
D) 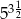
Liczba 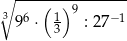 jest równa
jest równa
A) 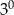 B)
B) 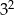 C)
C) 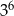 D)
D) 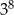
Wartość wyrażenia 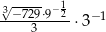 jest równa
jest równa
A) 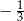 B)
B) 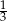 C) 1 D)
C) 1 D) 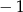
Liczba 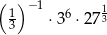 jest równa
jest równa
A) 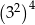 B)
B) 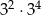 C)
C) 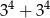 D)
D) 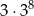
Liczba 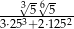 jest równa
jest równa
A) 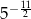 B)
B) 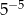 C)
C) 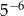 D)
D) 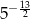
Liczba 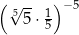 jest równa
jest równa
A) 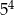 B)
B) 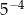 C)
C) 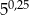 D)
D) 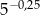
Liczba 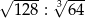 jest równa
jest równa
A) 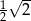 B) 2 C)
B) 2 C) 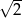 D)
D) 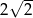
Liczba 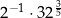 jest równa
jest równa
A) 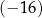 B)
B) 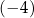 C) 2 D) 4
C) 2 D) 4
Liczba 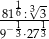 jest równa
jest równa
A) 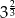 B)
B) 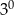 C)
C) 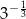 D)
D) 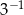
Jeżeli liczbę 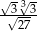 zapiszemy w postaci
zapiszemy w postaci 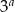 , to
, to  jest równe
jest równe
A)  B)
B) 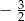 C)
C)  D)
D) 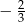
Wartość wyrażenia 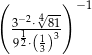 jest równa
jest równa
A) 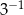 B)
B) 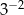 C)
C) 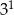 D)
D) 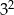
Liczba 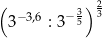 jest równa
jest równa
A) 0,9 B) 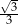 C)
C) 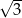 D)
D) 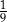
Liczba 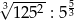 jest równa
jest równa
A) 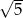 B)
B) 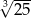 C)
C) 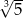 D) 5
D) 5
Liczba 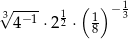 jest równa:
jest równa:
A) 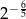 B)
B) 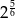 C)
C) 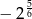 D)
D) 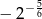
Liczba 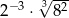 jest równa
jest równa
A) 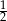 B) 1 C) 2 D) 4
B) 1 C) 2 D) 4
Liczba 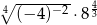 jest równa
jest równa
A) 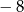 B) 8 C)
B) 8 C) 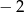 D) 4
D) 4
Liczbę 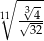 można zapisać w postaci
można zapisać w postaci
A) 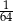 B)
B) 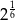 C)
C) 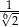 D)
D) 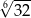
Liczba 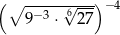 jest równa
jest równa
A) 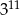 B)
B) 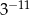 C)
C) 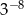 D)
D) 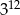
Iloraz 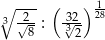 jest równy
jest równy
A) 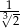 B)
B) 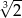 C) 1 D)
C) 1 D) 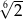
Wartość wyrażenia 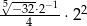 jest równa
jest równa
A) 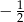 B)
B) 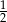 C) 1 D)
C) 1 D) 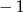
Liczba 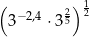 jest równa
jest równa
A) 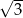 B)
B) 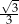 C)
C) 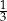 D) 0,3
D) 0,3
Liczba 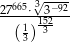 jest równa
jest równa
A) 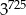 B)
B) 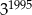 C)
C) 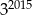 D)
D) 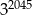
Liczba 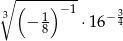 jest równa
jest równa
A) 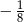 B)
B) 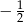 C)
C) 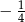 D)
D) 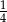
Liczba 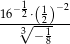 jest równa
jest równa
A) 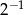 B)
B) 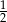 C)
C) 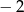 D) 1
D) 1
Wyrażenie 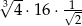 zapisane w postaci potęgi liczby 2, to
zapisane w postaci potęgi liczby 2, to
A) 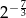 B)
B) 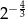 C)
C) 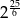 D)
D) 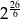
Liczba 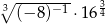 jest równa
jest równa
A) 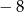 B)
B) 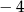 C) 2 D) 4
C) 2 D) 4
Liczba 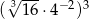 jest równa
jest równa
A) 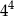 B)
B) 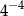 C)
C) 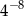 D)
D) 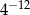
Wartość wyrażenia 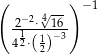 jest równa
jest równa
A) 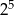 B)
B) 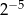 C)
C) 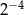 D)
D) 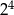
Liczba 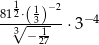 jest równa
jest równa
A) 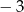 B)
B) 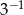 C)
C) 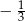 D) 3
D) 3

