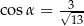Dziedziną funkcji 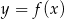 jest przedział
jest przedział 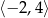 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 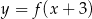 jest zbiór
jest zbiór
A) 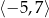 B)
B) 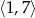 C)
C) 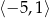 D)
D) 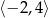
/Szkoła średnia/Zadania testowe/Funkcje
Dziedziną funkcji 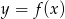 jest przedział
jest przedział 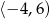 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 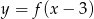 jest zbiór
jest zbiór
A) 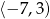 B)
B) 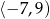 C)
C) 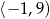 D)
D) 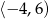
Dziedziną funkcji 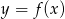 jest przedział
jest przedział 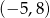 . Zatem dziedziną funkcji
. Zatem dziedziną funkcji 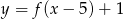 jest przedział
jest przedział
A) 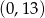 B)
B) 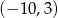 C)
C) 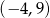 D)
D) 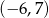
Funkcja 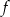 każdej liczbie naturalnej ze zbioru
każdej liczbie naturalnej ze zbioru 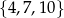 przyporządkowywuje resztę z dzielenia tej liczby przez 3. Zbiorem wartości tej funkcji jest zbiór
przyporządkowywuje resztę z dzielenia tej liczby przez 3. Zbiorem wartości tej funkcji jest zbiór
A) 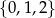 B)
B) 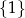 C)
C) 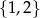 D)
D) 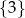
Funkcja 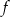 każdej liczbie naturalnej ze zbioru
każdej liczbie naturalnej ze zbioru 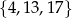 przyporządkowywuje resztę z dzielenia tej liczby przez 5. Zbiorem wartości tej funkcji jest zbiór
przyporządkowywuje resztę z dzielenia tej liczby przez 5. Zbiorem wartości tej funkcji jest zbiór
A) 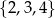 B)
B) 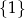 C)
C) 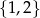 D)
D) 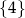
Funkcja 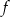 każdej liczbie naturalnej ze zbioru
każdej liczbie naturalnej ze zbioru 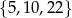 przyporządkowywuje resztę z dzielenia tej liczby przez 4. Zbiorem wartości tej funkcji jest zbiór
przyporządkowywuje resztę z dzielenia tej liczby przez 4. Zbiorem wartości tej funkcji jest zbiór
A) 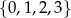 B)
B) 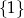 C)
C) 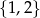 D)
D) 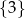
Wartość wyrażenia 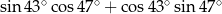 jest równa
jest równa
A) 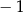 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Wartość wyrażenia 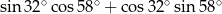 jest równa
jest równa
A) 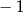 B) 1 C) 0 D) 2
B) 1 C) 0 D) 2
Wartość wyrażenia 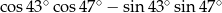 jest równa
jest równa
A) 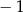 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Liczba 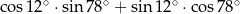 jest równa
jest równa
A) 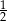 B)
B) 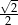 C)
C) 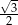 D) 1
D) 1
Wartość wyrażenia 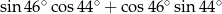 jest równa
jest równa
A) 1 B) 0 C) 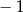 D) 2
D) 2
Funkcja 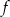 jest określona wzorem
jest określona wzorem 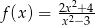 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 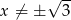 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 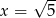 jest równa
jest równa
A) 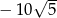 B)
B) 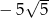 C)
C) 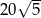 D)
D) 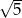
Funkcja 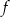 jest określona wzorem
jest określona wzorem 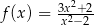 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 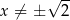 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 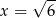 jest równa
jest równa
A) 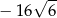 B)
B) 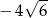 C)
C) 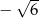 D)
D) 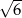
Wartość wyrażenia 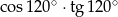 wynosi
wynosi
A) 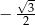 B) 1 C)
B) 1 C) 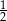 D)
D) 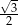
Wielomian 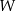 określony wzorem
określony wzorem 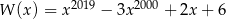
A) jest podzielny przez 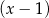 i z dzielenia przez
i z dzielenia przez 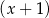 daje resztę równą 6.
daje resztę równą 6.
B) jest podzielny przez 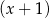 i z dzielenia przez
i z dzielenia przez 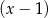 daje resztę równą 6.
daje resztę równą 6.
C) jest podzielny przez 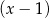 i jest podzielny przez
i jest podzielny przez 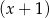 .
.
D) nie jest podzielny ani przez 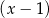 , ani przez
, ani przez 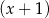 .
.
Wielomian 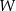 określony wzorem
określony wzorem 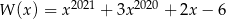
A) jest podzielny przez 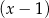 i z dzielenia przez
i z dzielenia przez 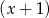 daje resztę równą
daje resztę równą 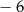 .
.
B) jest podzielny przez 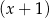 i z dzielenia przez
i z dzielenia przez 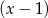 daje resztę równą
daje resztę równą 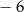 .
.
C) jest podzielny przez 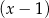 i jest podzielny przez
i jest podzielny przez 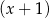 .
.
D) nie jest podzielny ani przez 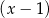 , ani przez
, ani przez 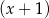 .
.
Reszta z dzielenia wielomianu 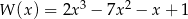 przez dwumian
przez dwumian 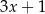 jest równa
jest równa
A) 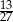 B)
B) 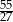 C)
C) 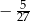 D)
D) 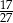
Reszta z dzielenia wielomianu 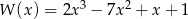 przez dwumian
przez dwumian 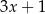 jest równa
jest równa
A) 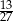 B)
B) 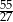 C)
C) 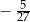 D)
D) 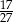
Wielomian 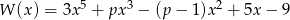 jest podzielny przez dwumian
jest podzielny przez dwumian 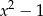 dla
dla 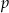 równego
równego
A) 6 B) 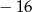 C) 4 D)
C) 4 D) 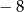
Wartość wyrażenia 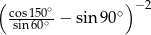 jest równa
jest równa
A) 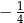 B)
B) 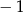 C) 1 D)
C) 1 D) 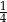
Wartość wyrażenia 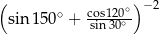 jest równa
jest równa
A) 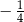 B) 4 C) 1 D)
B) 4 C) 1 D) 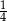
Funkcja 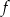 ma dwa miejsca zerowe 3 oraz
ma dwa miejsca zerowe 3 oraz 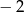 . Zatem funkcja
. Zatem funkcja 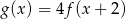
A) ma dwa miejsca zerowe 5 oraz 0
B) ma dwa miejsca zerowe 1 oraz 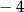
C) ma dwa miejsca zerowe 4 oraz 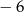
D) nie ma miejsc zerowych
Funkcja 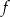 ma dwa miejsca zerowe 3 oraz
ma dwa miejsca zerowe 3 oraz 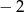 . Zatem funkcja
. Zatem funkcja 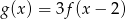
A) ma dwa miejsca zerowe 5 oraz 0
B) ma dwa miejsca zerowe 1 oraz 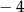
C) ma dwa miejsca zerowe 4 oraz 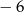
D) nie ma miejsc zerowych
Funkcja 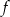 przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od
przyporządkowuje każdej liczbie naturalnej większej od 1 liczbę liczb pierwszych mniejszych od  . Liczba
. Liczba 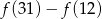 jest równa
jest równa
A) 5 B) 6 C) 4 D) 10
Funkcja 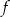 jest określona wzorem
jest określona wzorem 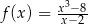 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 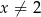 . Wartość pochodnej tej funkcji dla argumentu
. Wartość pochodnej tej funkcji dla argumentu 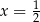 jest równa
jest równa
A) 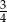 B)
B) 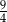 C) 3 D)
C) 3 D) 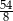
Dla każdego kąta  wyrażenie
wyrażenie 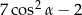 jest równe
jest równe
A) 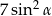 B)
B) 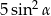
C)  D)
D) 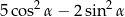
Liczba 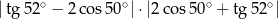 jest równa
jest równa
A) 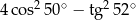 B)
B) 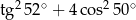
C) 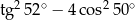 D)
D) 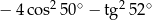
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 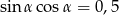 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 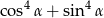 jest równa
jest równa
A) 1 B) 0,5 C) 0,25 D) 0,75
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 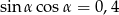 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 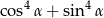 jest równa
jest równa
A) 0,68 B) 0,84 C) 0,32 D) 0,16
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 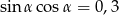 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 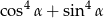 jest równa
jest równa
A) 0,18 B) 0,91 C) 0,82 D) 0,75
Poniżej zamieszczono fragment tabeli wartości funkcji liniowej
 | 1 | 2 | 4 |
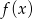 | 4 | 1 |
W pustym miejscu w tabeli powinna znajdować się liczba:
A) 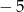 B) 5 C)
B) 5 C) 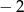 D) 2
D) 2
Funkcja 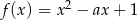 przyjmuje wartości mniejsze niż
przyjmuje wartości mniejsze niż 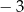 dla
dla
A) 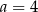 B)
B) 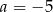 C)
C) 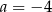 D)
D) 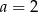
Jeżeli 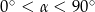 oraz
oraz 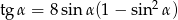 , to
, to
A) 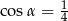 B)
B) 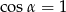 C)
C) 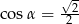 D)
D) 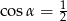
Jeżeli 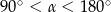 oraz
oraz 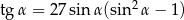 , to
, to
A) 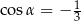 B)
B) 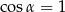 C)
C) 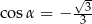 D)
D) 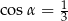
Granica 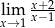
A) jest równa 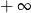 B) nie istnieje C) jest liczbą rzeczywistą D) jest równa
B) nie istnieje C) jest liczbą rzeczywistą D) jest równa 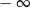
Granica 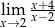
A) jest liczbą rzeczywistą B) jest równa 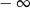 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 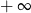
Granica 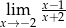
A) jest równa 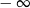 B) jest równa
B) jest równa 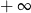 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica 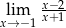
A) jest równa 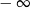 B) jest liczbą rzeczywistą C) jest równa
B) jest liczbą rzeczywistą C) jest równa 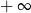 D) nie istnieje
D) nie istnieje
Granica 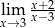
A) jest równa 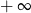 B) jest równa
B) jest równa 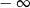 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica 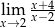
A) jest liczbą rzeczywistą B) jest równa 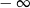 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 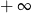
Granica 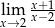
A) jest równa 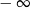 B) nie istnieje C) jest liczbą rzeczywistą D) jest równa
B) nie istnieje C) jest liczbą rzeczywistą D) jest równa 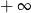
Granica 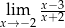
A) nie istnieje B) jest równa 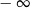 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 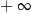
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 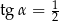 . Zatem
. Zatem
A) 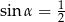 i
i 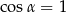 B)
B) 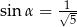 i
i 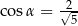
C) 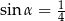 i
i 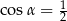 D)
D) 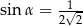 i
i 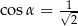
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 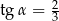 . Zatem
. Zatem
A) 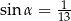 i
i 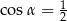 B)
B) 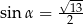 i
i 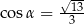
C) 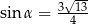 i
i 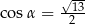 D)
D) 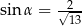 i
i