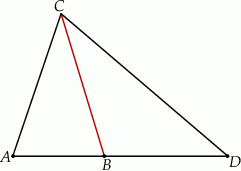
Punkty 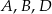 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 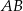 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego  (zobacz rysunek).
(zobacz rysunek).
Jeżeli 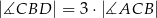 , to
, to 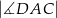 wynosi
wynosi
A) 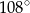 B)
B) 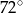 C)
C) 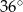 D)
D) 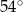
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 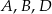 leżą na jednej prostej. Odcinek
leżą na jednej prostej. Odcinek 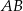 jest podstawą trójkąta równoramiennego
jest podstawą trójkąta równoramiennego  (zobacz rysunek).
(zobacz rysunek).

Jeżeli 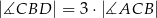 , to
, to 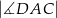 wynosi
wynosi
A) 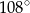 B)
B) 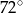 C)
C) 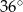 D)
D) 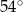
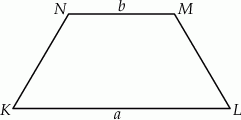
Dany jest trapez równoramienny 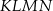 , którego podstawy mają długości
, którego podstawy mają długości 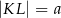 ,
, 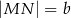 ,
, 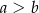 . Kąt
. Kąt 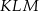 ma miarę
ma miarę 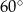 . Długość ramienia
. Długość ramienia 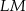 tego trapezu jest równa
tego trapezu jest równa
A) 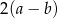 B)
B) 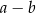 C)
C) 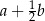 D)
D) 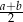
W trapezie równoramiennym 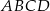 podstawy
podstawy 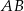 i
i 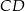 mają długości równe odpowiednio
mają długości równe odpowiednio  i
i 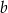 (przy czym
(przy czym 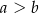 ). Miara kąta ostrego trapezu jest równa
). Miara kąta ostrego trapezu jest równa 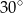 . Wtedy wysokość tego trapezu jest równa
. Wtedy wysokość tego trapezu jest równa
A) 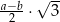 B)
B) 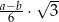 C)
C) 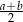 D)
D) 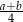
Dany jest trójkąt o bokach długości 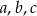 . Stosunek
. Stosunek 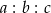 jest równy 3:5:7. Które zdanie jest fałszywe?
jest równy 3:5:7. Które zdanie jest fałszywe?
A) Liczba  jest o 12,5% mniejsza od liczby
jest o 12,5% mniejsza od liczby 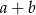
B) Liczba  stanowi 20% liczby
stanowi 20% liczby 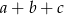
C) Liczba  stanowi 25% liczby
stanowi 25% liczby 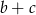
D) Liczba 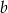 to 60% liczby
to 60% liczby  .
.
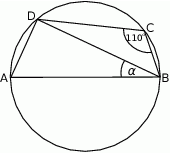
Miara kąta  , zaznaczonego na rysunku, jest równa
, zaznaczonego na rysunku, jest równa
A) 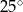 B)
B) 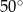 C)
C) 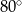 D)
D) 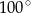
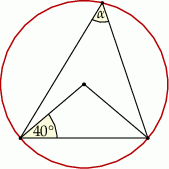
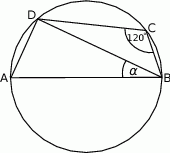
Punkty 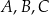 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 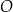 . Kąt
. Kąt 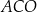 ma miarę
ma miarę 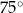 (zobacz rysunek).
(zobacz rysunek).
Miara kąta ostrego 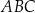 jest równa
jest równa
A) 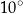 B)
B) 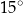 C)
C) 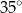 D)
D) 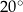
Punkty 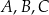 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 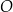 . Kąt
. Kąt 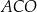 ma miarę
ma miarę 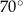 (zobacz rysunek).
(zobacz rysunek).
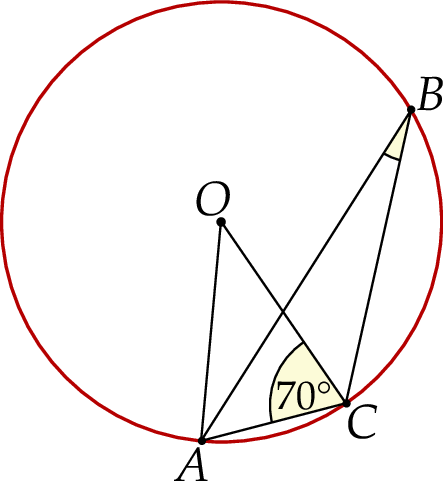
Miara kąta ostrego  jest równa
jest równa
A)  B)
B)  C)
C) 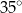 D)
D) 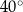
Miara kąta  , zaznaczonego na rysunku, jest równa
, zaznaczonego na rysunku, jest równa
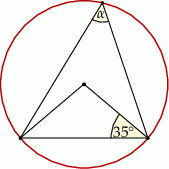
A) 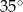 B)
B) 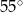 C)
C) 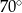 D)
D) 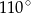
Punkty 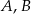 oraz
oraz 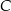 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 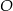 . Kąt
. Kąt 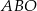 ma miarę
ma miarę 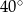 , a kąt
, a kąt  ma miarę
ma miarę  (zobacz rysunek).
(zobacz rysunek).
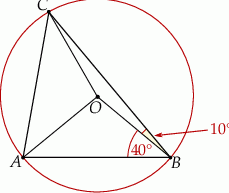
Miara kąta  jest równa
jest równa
A) 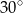 B)
B) 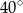 C)
C) 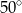 D)
D) 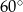
Punkty 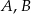 oraz
oraz 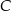 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 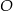 . Kąt
. Kąt 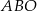 ma miarę
ma miarę 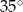 , a kąt
, a kąt 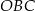 ma miarę
ma miarę 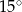 (zobacz rysunek).
(zobacz rysunek).
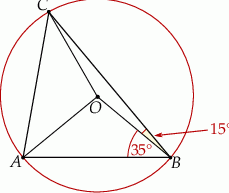
Miara kąta 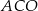 jest równa
jest równa
A) 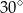 B)
B) 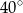 C)
C) 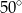 D)
D) 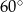
Pole powierzchni równoległoboku jest równe 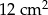 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 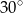 . Wiadomo, że dwa boki równoległoboku mają długość 3 cm. Długość pozostałych boków jest równa:
. Wiadomo, że dwa boki równoległoboku mają długość 3 cm. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
Pole powierzchni równoległoboku jest równe 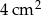 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 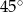 . Wiadomo, że dwa boki równoległoboku mają długość
. Wiadomo, że dwa boki równoległoboku mają długość 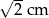 . Długość pozostałych boków jest równa:
. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
Pole powierzchni równoległoboku jest równe 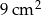 , a kąt ostry równoległoboku ma miarę
, a kąt ostry równoległoboku ma miarę 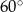 . Wiadomo, że dwa boki równoległoboku mają długość
. Wiadomo, że dwa boki równoległoboku mają długość 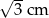 . Długość pozostałych boków jest równa:
. Długość pozostałych boków jest równa:
A) 2 cm B) 4 cm C) 6 cm D) 8 cm
Pole czworokąta przedstawionego na rysunku jest równe
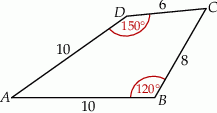
A) 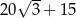 B)
B) 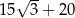 C)
C) 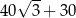 D)
D) 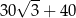
Trapez 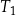 , o polu równym 52 i obwodzie 36, jest podobny do trapezu
, o polu równym 52 i obwodzie 36, jest podobny do trapezu 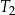 . Pole trapezu
. Pole trapezu 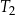 jest równe 13. Obwód trapezu
jest równe 13. Obwód trapezu 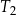 jest równy
jest równy
A) 18 B) 9 C) 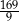 D)
D) 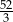
Czworokąt 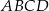 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 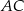 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 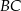 i
i 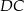 , a kąt
, a kąt 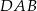 ma miarę
ma miarę 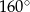 .
.
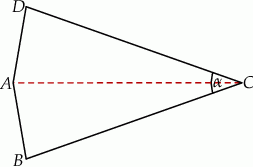
Miara kąta 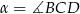 jest równa
jest równa
A) 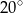 B)
B) 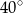 C)
C) 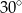 D)
D) 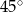
Miary dwóch kątów trapezu równoramiennego pozostają w stosunku 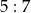 . Wynika stąd, że największy kąt tego trapezu ma miarę
. Wynika stąd, że największy kąt tego trapezu ma miarę
A) 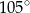 B)
B) 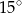 C)
C) 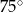 D)
D) 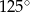
Obwód trójkąta 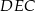 wynosi
wynosi 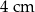 . Wiadomo, że
. Wiadomo, że 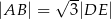 oraz
oraz 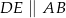 . Zatem obwód trójkąta
. Zatem obwód trójkąta  jest równy
jest równy
A) 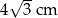 B)
B) 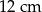 C)
C) 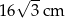 D)
D) 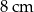
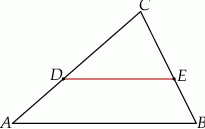
Obwód trójkąta 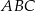 jest równy 40 cm. Punkt
jest równy 40 cm. Punkt 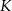 leży na boku
leży na boku 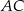 , a punkt
, a punkt 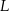 na boku
na boku 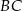 tak, że odcinek
tak, że odcinek 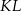 jest równoległy do boku
jest równoległy do boku 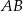 trójkąta i
trójkąta i 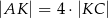 . Obwód trójkąta
. Obwód trójkąta 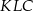 jest równy:
jest równy:
A) 10 cm B) 4 cm C) 8 cm D) 5 cm
Pole figury 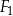 złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury
złożonej z dwóch stycznych zewnętrznie kół o promieniach 1 i 3 jest równe polu figury 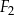 złożonej z dwóch stycznych zewnętrznie kół o promieniach długości
złożonej z dwóch stycznych zewnętrznie kół o promieniach długości  (zobacz rysunek).
(zobacz rysunek).
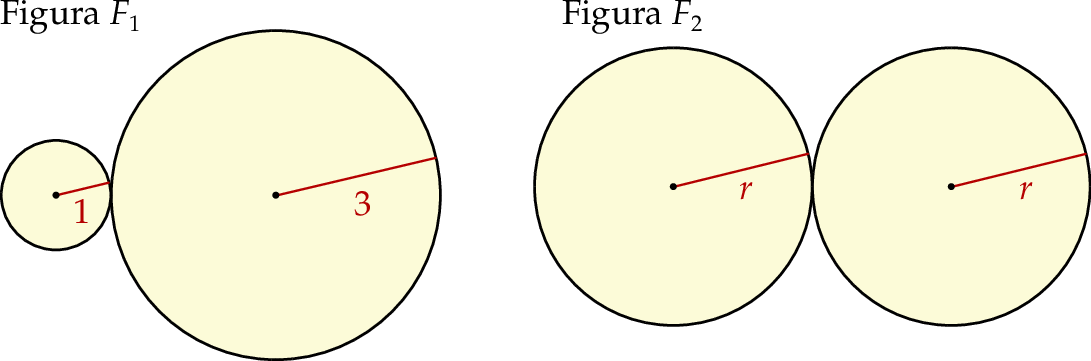
Długość  promienia jest równa
promienia jest równa
A) 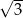 B) 2 C)
B) 2 C) 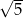 D) 3
D) 3
Pole figury  złożonej z dwóch stycznych zewnętrznie kół o promieniach 3 i 5 jest równe polu figury
złożonej z dwóch stycznych zewnętrznie kół o promieniach 3 i 5 jest równe polu figury 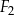 złożonej z dwóch stycznych zewnętrznie kół o promieniach długości
złożonej z dwóch stycznych zewnętrznie kół o promieniach długości  (zobacz rysunek).
(zobacz rysunek).
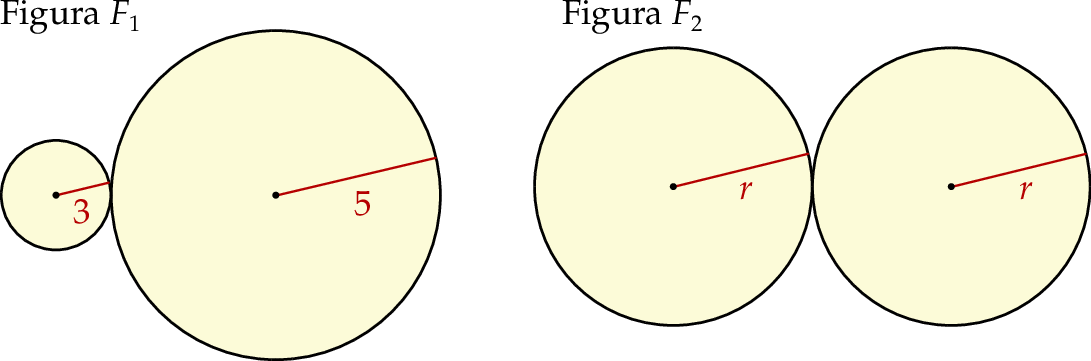
Długość  promienia jest równa
promienia jest równa
A) 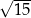 B) 4 C)
B) 4 C) 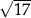 D) 6
D) 6
Pole trójkąta, w którym wysokość jest o 3 cm dłuższa od podstawy jest równe 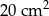 Wysokość trójkąta jest równa:
Wysokość trójkąta jest równa:
A) 5 cm B) 8 cm C) 2 cm D) 11 cm
Jeżeli środek okręgu opisanego na trójkącie leży na wysokości trójkąta, to trójkąt ten musi być
A) równoboczny B) równoramienny C) prostokątny D) rozwartokątny
Jeżeli środek okręgu wpisanego w trójkąt leży na wysokości trójkąta, to trójkąt ten musi być
A) rozwartokątny B) prostokątny C) równoramienny D) równoboczny
Bok 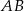 czworokąta
czworokąta 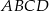 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 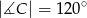 .
.
Zatem kąt  ma miarę
ma miarę
A) 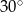 B)
B) 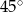 C)
C) 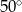 D)
D) 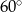
Bok 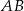 czworokąta
czworokąta 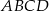 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 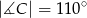 .
.
Zatem kąt  ma miarę
ma miarę
A) 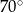 B)
B) 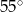 C)
C) 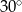 D)
D) 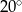
Przekątne rombu mają długości 8 i 14. Obwód tego rombu jest równy
A) 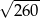 B)
B) 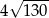 C)
C) 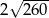 D)
D) 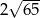
Przekątne rombu mają długości 12 i 10. Obwód tego rombu jest równy
A) 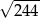 B)
B) 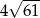 C)
C) 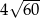 D)
D) 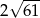
Pole kwadratu 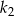 jest o 21% większe od pola kwadratu
jest o 21% większe od pola kwadratu 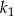 . Wówczas długość boku kwadratu
. Wówczas długość boku kwadratu 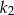 jest większa od długości boku kwadratu
jest większa od długości boku kwadratu 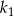 o
o
A) 10% B) 110% C) 21% D) 121%
Dane są dwa prostokąty: 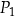 oraz
oraz 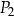 . Długości boków prostokąta
. Długości boków prostokąta 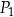 są równe
są równe  oraz
oraz 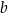 . Długości boków prostokąta
. Długości boków prostokąta 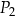 są równe
są równe 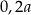 oraz
oraz 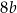 . Pole prostokąta
. Pole prostokąta 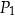 stanowi
stanowi
A) 60% pola prostokąta 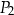 .
.
B) 62,5% pola prostokąta 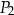 .
.
C) 160% pola prostokąta 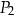 .
.
D) 162,5% pola prostokąta 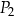 .
.
Odcinki 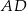 i
i 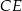 są wysokościami trójkąta
są wysokościami trójkąta 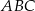 .
.
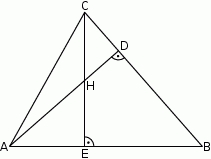
Zatem
A) 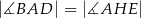 B)
B) 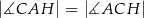
C) 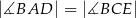 D)
D) 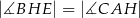
W trójkącie stosunek miar kątów jest równy 3:4:5. Zatem najmniejszy kąt tego trójkąta ma miarę
A) 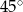 B)
B) 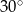 C)
C) 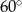 D)
D) 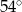
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 3:4:5. Najmniejszy kąt wewnętrzny tego trójkąta ma miarę
A) 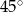 B)
B) 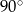 C)
C) 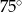 D)
D) 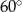
Miary kątów wewnętrznych pewnego trójkąta pozostają w stosunku 2:4:9. Największy kąt wewnętrzny tego trójkąta ma miarę
A) 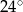 B)
B) 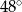 C)
C) 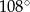 D)
D) 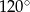
Dwa trójkąty podobne mają pola równe odpowiednio 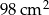 ,
, 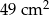 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 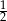 B) 2 C) 4 D)
B) 2 C) 4 D) 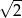
Dwa trójkąty podobne mają pola równe odpowiednio 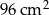 ,
, 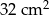 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 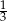 B)
B) 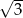 C) 9 D) 3
C) 9 D) 3
Dwa trójkąty podobne mają pola równe odpowiednio 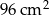 ,
, 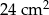 . Skala podobieństwa jest równa
. Skala podobieństwa jest równa
A) 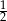 B) 4 C) 2 D)
B) 4 C) 2 D) 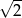
Jeżeli trójkąty 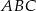 i
i 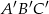 są podobne, a ich pola są, odpowiednio, równe
są podobne, a ich pola są, odpowiednio, równe 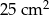 i
i 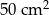 , to skala podobieństwa
, to skala podobieństwa 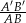 jest równa
jest równa
A) 2 B) 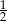 C)
C) 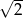 D)
D) 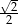
Trójkąt 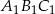 o polu
o polu 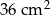 jest podobny do trójkąta
jest podobny do trójkąta 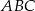 o polu
o polu 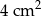 . Skala podobieństwa trójkąta
. Skala podobieństwa trójkąta 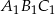 do trójkąta
do trójkąta 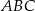 jest równa
jest równa
A) 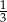 B) 9 C) 12 D) 3
B) 9 C) 12 D) 3
